数据结构——二叉树（超详细，递归，前中后序遍历，附代码）

最新推荐文章于 2024-10-25 16:10:03 发布

原创最新推荐文章于 2024-10-25 16:10:03 发布 · 1.1k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #c语言 #linux

本文介绍了树的基本概念，包括递归定义、节点度、层次和深度，重点讨论了二叉树的特性（如满二叉树和完全二叉树），并给出了顺序存储和链式存储二叉树的实现以及三种基本遍历方法（先序、中序和后序）。

树

定义：递归的定义，由n个节点的有限集合，这个集合有且只有一个根节点（没有直接前

驱），所有节点都是一个子树且互不相交

节点度：子节点的个数树的度：最大节点度数

层次：根节点为第一层依次加一

树的深度：最大层次

叶子节点/外部节点：度为0

分支节点/内部节点：度不为0

二叉树

定义

n个节点的有限集合，有且只有一个根节点，和左右两颗子树，且子树也是一颗二叉

树，且严格区分左右子树

特点：第i层最多有 2^(i-1) 个节点，一个深度为i的树，节点总数最多有2^i - 1个叶子节点的个数比度为2的节点个数多一个

满二叉树：

一个深度为i的树，节点总数有2^i - 1个

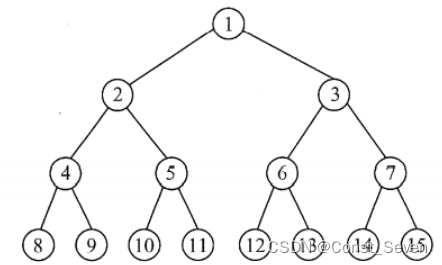
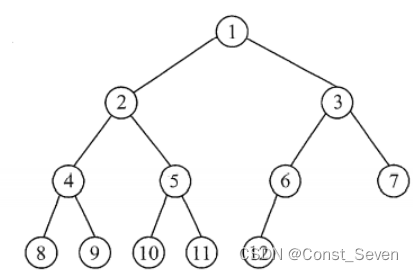
完全二叉树：

只有最后两层有度不为2的结点，且叶子节点左边连续

具有n个节点的完全二叉树的深度为（log2n）＋1或『log2(n+1)。

顺序存储二叉树实现：

#include <stdio.h>
#include <stdlib.h>

typedef char sqt_data_t;

#define SIZE 1024

typedef struct sqtree
{
	sqt_data_t data[SIZE];
	int len;
}sqt_node, *sqt_pnode;

sqt_pnode space_tree()
{
	sqt_pnode T = (sqt_pnode)malloc(sizeof(sqt_node));
	if(NULL == T)
		return NULL;
	
	T->len = 0;
	
	return T;
}
//创建二叉树
sqt_pnode create_tree(sqt_pnode T,  int index)
{
	sqt_data_t data;
	
	scanf("%c", &data);
	getchar();
	T->len++;
	if(data == '#')
		return NULL;
	//创建根
	T->data[index] = data;
	//创建左子树
	create_tree(T, 2*index + 1);
	//创建右子树
	create_tree(T, 2*index + 2);
	
	return T;
}

void show_sqtree(sqt_pnode T)
{
	int i;
	for(i = 0; i < T->len; i++)
	{
		printf("%c\n", T->data[i]);
	}
	return ;
}
int main()
{
	sqt_pnode T = space_tree();
	
	create_tree(T, 0);
	
	show_sqtree(T);
	
	return 0;
}

链式存储二叉树实现：

头文件

#ifndef _LINKTREE_H
#define _LINKTREE_H

typedef char lkt_data_t;

typedef struct linktree{
	lkt_data_t data;
	struct linktree *lchild ;
	struct linktree *rchild ;
}lkt_node,*lkt_pnode;	

lkt_pnode create_linktree();

int preorder_linktree(lkt_pnode T);

int inorder_linktree(lkt_pnode T);

int postorder_linktree(lkt_pnode T);

int leveorder_linktree(lkt_pnode T);

#endif

函数功能实现

#include <stdio.h>
#include <stdlib.h>
#include "linktree.h"
#include "linkqueue.h"

lkt_pnode create_linktree()
{
    lkt_data_t data;
    scanf("%c", &data);
    getchar();
    if('#' == data)
        return NULL;
    //根
    lkt_pnode T = (lkt_pnode)malloc(sizeof(lkt_node));
    if(NULL == T)
        return NULL;

    T->data = data;
    //左子树
    T->lchild = create_linktree();
    //右子树的创建
    T->rchild = create_linktree();

    return T;
}

int leveorder_linktree(lkt_pnode T)
{
    //创建链队列
    lkq_pnode Q = create_linkqueue();
    if(NULL == Q)
        return -1;
    
	input_linkqueue(Q, T);
    while(0 != empty_linkqueue(Q))
    {
        printf("%c\n",output_linkqueue(Q));
        if(NULL != data->lchild)
           input_linkqueue(Q, data->lchild));
        if(NULL != data->rchild)
           input_linkqueue(Q, data->rchild));
    }

    return 0;
}

二叉树的遍历

从根结点出发，按照次序访问二叉树中所有结点，使得每个结点仅被访问一次。

1、先序遍历

访问根节点
遍历左子树

遍历右子树

int preorder_linktree(lkt_pnode T)
{
    if(NULL == T)
        return -1;

    //根
    printf("%c\n", T->data);
    //左子树
    preorder_linktree(T->lchild);
    //右子树
    preorder_linktree(T->rchild);

    return 0;
}

2、中序遍历

遍历左子树
访问根节点

遍历右子树

int inorder_linktree(lkt_pnode T)
{
    if(NULL == T)
        return -1;


    //左子树
    inorder_linktree(T->lchild);
    //根
    printf("%c\n", T->data);
    //右子树
    inorder_linktree(T->rchild);

    return 0;
}

3、后序遍历

遍历左子树
遍历右子树

访问根节点

int postorder_linktree(lkt_pnode T)
{
    if(NULL == T)
        return -1;


    //左子树
    postorder_linktree(T->lchild);

    //右子树
    postorder_linktree(T->rchild);

    //根
    printf("%c\n", T->data);

    return 0;
}