题目大意:只允许使用加、取反(添负号)、偏移(加减一个常数)、左右移位(乘或除以 22 的非负整数次幂)和神奇的 �(�)S(x) 函数来进行编程,造一台计算机,构造一个计算网络,完成 1010 项指定的计算任务。要求计算次数尽可能少。
其中 �(�)S(x) 函数为 11+�−�1+e−x1 ,是一个非线性的函数。
�(�)S(x) 函数全名是 SigmoidSigmoid 函数,又称 “�S 型生长曲线” 。
�=�(�)y=S(x) 的图像:
还有三个功能强大但是使用了会扣分的计算节点:比较节点、取两数最大值节点、乘法节点。
是一道提交答案题。
题目补充。
解法:构造答案
具体解法在各个 tasktask 中介绍。
本题主要就是 1010 个计算网络的构造。
核心思想就是:利用好 �(�)S(x) 的选择性。用 �(�)S(x) 来实现比较大小、取 00 取 11 ,制造分段函数,是这道题的关键所在。
必要的地方加一些小优化,以减少计算节点数。
本题解对解题过程中所用到的所有参数进行了我自认为比较详细地分析,希望这些分析能帮到阅读本题解的你。
task1task1
要求
输入:�,�a,b 。
输入限制:∣�∣,∣�∣⩽109∣a∣,∣b∣⩽109 ,小数部分不超过 99 位。
输出:−2�−2�−2a−2b 。
满分行数:66 行。
解决方法
送分点。
一般来说,我们都会想到提取公因数 −2−2 来减少运算次数。
一般来说,我们也都会想到用左移 11 位来计算乘 22 这个操作。
输出代码
if(n==1) { // 6行。
printf("I\n");
printf("I\n");
printf("+ 1 2\n");
printf("< 3 1\n");
printf("- 4\n");
printf("O 5");
}
task2task2
要求
输入:�a 。
输入限制:∣�∣⩽109∣a∣⩽109 ,小数部分不超过 99 位。
输出:11+�17�1+e17a1 。
满分行数:66 行。
解决方法
也是送分点。
观察输出的这个表达式的样子,显然这个点是要用 �(�)S(x) 函数的。
然后,注意到 17�=16�+�=24�+�17a=16a+a=24a+a ,所以我们可以用位移和加法来解决乘法了。
最后还得小心,�(�)=11+�−�S(x)=1+e−x1 ,还得将 17�17a 取反后使用 �S 函数。
输出代码
if(n==2) { // 6行。
printf("I\n");
printf("< 1 4\n");
printf("+ 1 2\n");
printf("- 3\n");
printf("S 4\n");
printf("O 5");
}
task3task3
要求
输入:�a 。
输入限制:∣�∣⩽109∣a∣⩽109 ,小数部分不超过 99 位。
输出:sign(�)={−1,�<0 0,�=0 1,�>0sign(a)=⎩⎪⎪⎨⎪⎪⎧−1,a<0 0,a=0 1,a>0 。
满分行数:66 行。
解决方法
不是送分了。开始有难度了。
没有除法,所以 �∣�∣∣a∣a 泡汤了。况且求 ∣�∣∣a∣ 是下一个 tasktask 的任务,所以按道理说应该并不容易求。
使用比较语句的话,直接与 00 做比较,输出比较的值即可。可得 66 分。
可以用 �×2−1000a×2−1000 来造 00 。之后就可以用比较节点比较 �a 和 00 的大小。
但是如何使用基本操作来搞出答案呢?
我们是该想想怎么用 �S 函数了。
回顾题目
其实,我们在读题面过程中,会发现计算过程中数据精度特别高:小数点后 9090 位,整数部分绝对值不超过 101000101000。
而最终
Special Judge判定结果时,只要与标准答案的结果相差小于 10−910−9 即可。
为什么给如此大的精度?尤其是整数部分,为何那么大?小数部分似乎也精确得过分了,这又是为什么?
而且,为什么 �S 函数一定要用 11+�−�1+e−x1 ?它有什么特殊之处吗?
观察发现,除了第二个测试点需要直接使用了 �(�)S(x) 来求出 11+�17�1+e17a1 精确值之外,其余九个测试点表面上似乎都没有涉及到 �(�)S(x) 的使用。
出题人如果只是为了送分的话,为什么还要搞这么一个函数出来呢?这个函数真的没有其他作用了吗?
仔细想想,我们察觉到,好像确实没有哪个测试点需要使用 �(�)S(x) 的精确值了。所以,�(�)S(x) 的价值,难道是体现在其近似值上面了吗?
种种不同寻常的地方提醒着我们,这道题必然要涉及到极限的问题,即我们要通过某些操作,爆掉 9090 位小数的精度,以此模拟取极限的过程。而 �S 函数的特殊之处就在于,它在正负无穷大处都有极限,分别为 11 和 00 ,而 �=�(�)y=S(x) 图像上有唯一一个横纵坐标都是有理数的点 (0,12)(0,21) ,这也是 �(�)S(x) 的性质。进一步的, �(�)+�(−�)=1S(x)+S(−x)=1 ,同样是一条性质。
这就启示我们结合 lim�→+∞�(�)=1x→+∞limS(x)=1 , lim�→−∞�(�)=0x→−∞limS(x)=0 ,和 �(0)=12S(0)=21 这三条性质,来完成题目。
�(�)S(x) 的两个极限: 11 和 00 ,恰好对应了“真”和“假”两种状态。这个性质,某种意义上而言,是实现“比较”操作的方法,能够用来判别正负。
所以 �S 函数与极限结合,应该是这道题考察的重点之一。
怎么利用 �S 函数呢?
既然要考虑极限,我们很容易想到,将 �S 函数乘 22 ,再减去 11,所得恰好是个在 +∞,−∞+∞,−∞ 处极限分别为 +1,−1+1,−1 的函数(即 21+�−�−11+e−x2−1)。而且在 �=0x=0 处,取值也恰好为 00 。
这么看来,我们应该构造对了。
那么如何取极限?
简单,左移个百来位就可以变得很大了,只要 �−�e−x 爆了 9090 位小数的精度,就能认为 �(�)S(x) 与 ±1±1 精确相等了。
大概多少位比较合适呢?
-
+∞+∞ 处的极限:
由 11+�−�<1−5×10−911+e−x1<1−5×10−91 ,
得 �−�<11−5×10−91−1e−x<1−5×10−911−1,
因为,当 ∣�∣<1∣x∣<1 时,根据等比数列求和公式和极限理论,有 11−�=1+�+�2+�3+⋯=∑�=0∞��>1+�1−x1=1+x+x2+x3+⋯=i=0∑∞xi>1+x 。这是因为 �2x2 必然是正数,而且比 �3x3 大,同理 �4x4 是正数,比 �5x5 大,以此类推,可知 11−�>1+�1−x1>1+x 成立。
所以 11−5×10−91−1>5×10−911−5×10−911−1>5×10−91 ,
那么,只需要 �−�<5×10−91e−x<5×10−91 即可。
得 −�<ln(5×10−91)=ln5−91ln10−x<ln(5×10−91)=ln5−91ln10 ,
于是 �>91ln10−ln5≈207.926x>91ln10−ln5≈207.926 ,
而 �a 最小是 10−910−9 ,只需解 2�×10−9>2082k×10−9>208 ,解得 �k 即可。
那么,�>log2(208×109)≈37.598k>log2(208×109)≈37.598 。
所以 �⩾38k⩾38 。
-
−∞−∞ 处的极限:
由 21+�−�<5×10−911+e−x2<5×10−91 ,
得 �−�>4×1090−1e−x>4×1090−1 , −�>ln(4×1090−1)−x>ln(4×1090−1) ,只需 −�>ln(4×1090)−x>ln(4×1090) ,
于是 �<−90ln10−ln4≈−208.619x<−90ln10−ln4≈−208.619 , �>log2(212×109)≈37.625k>log2(212×109)≈37.625 。
所以,左移 3838 位即可。
-
为什么不用偏移来制造无穷大呢?
因为偏移无法保持正负。
-
位移有上限,需解方程 2�×109<1010002k×109<101000 ,也就是 �<991log210≈3292.031k<991log210≈3292.031。所以 �=38k=38 没问题的。
输出代码
if(n==3) { // 6行。
printf("I\n");
printf("< 1 38\n");
printf("S 2\n");
printf("< 3 1\n");
printf("C 4 -1\n");
printf("O 5");
}
task4task4
要求
输入:�a 。
输入限制:∣�∣⩽109∣a∣⩽109 ,小数部分不超过 99 位。
输出:∣�∣∣a∣ ,即 �a 的绝对值。
满分行数:1414 行。
解决方法
��.�PS.a 乘 ����(�)sign(a) 是一种解决方法,可得 66 分。
我的思路和第三个点的差不多。
首先我想到,�=∣�∣y=∣x∣ 的图像关于 �y 轴对称,是个偶函数,而 �(�)+�(−�)=1S(x)+S(−x)=1 告诉我们,�(�)S(x) 图像关于 (0,12)(0,21) 对称。所以,怎么用 �(�)S(x) 搞出一个偶函数来?
�(�)S(x) 在正负无穷处函数变化率都趋于零,这启示我们使用导数。
经过验算,我发现,�′(�)=�−�(1+�−�)2S′(x)=(1+e−x)2e−x 是个偶函数,且 lim�→∞�′(�)=0x→∞limS′(x)=0 , �(0)=14S(0)=41 。
虽然这个导数同 ∣�∣∣x∣ 一样,是个偶函数;但是 ∣�∣∣x∣ 在 �x 趋于无穷时是无穷,而 �′(�)S′(x) 在 �x 趋于无穷时却趋于 00 。更糟的是,在 �=0x=0 的两侧,∣�∣∣x∣ 的表达式可写成不一样的形式,即 ∣�∣={ �,�>0 0,�=0−�,�<0∣x∣=⎩⎪⎪⎨⎪⎪⎧ x,x>0 0,x=0−x,x<0 ,而 �′(�)S′(x) 不能。
所以这样看来, �′(�)S′(x) 并不能很好的模拟 ∣�∣∣x∣ 函数。即使能够用 �′(�)S′(x) 构造,怕也免不了一些乘法或者比较的操作。
虽然用 �′(�)S′(x) 直接构造 ∣�∣∣x∣ 的思路失败了,但引入 �′(�)S′(x) 来辅助解题确实是一个良好的尝试。
况且,难道仅凭这一次尝试,就能断言 �′(�)S′(x) 毫无作用了吗?
事实上导数真的很有用。
我们用不了 �′(�)S′(x) 的全部,我们只考虑 �′(�)S′(x) 在一点处的取值。
在解决第三个点时,我们使用了 �(�)S(x) 的两个极限,那么做这个点时,不妨再考虑考虑,能不能使用 �(0)=12S(0)=21 这个性质。
由 �′(0)=14S′(0)=41 ,我们很容易写出 �(�)S(x) 在 �=0x=0 处的切线:�=14�+12y=41x+21 。
由切线的意义可知,�=�(�)y=S(x) 在 �=0x=0 附近与 �=14�+12y=41x+21 拟合得很好,
这样,我们就得到了一个关于 �x 的一次函数,且这个函数减去 1221 再乘 44 就能得到 �x 。
我们实际上得到的是一个从 �(�)S(x) 得到 �x 的办法,这个办法很重要。
其重要性在于,我们可以将获得 �x 的操作拆解为 �→�(�)→�x→S(x)→x 两个步骤,从而向这两个步骤中添加进一些我们想要的条件。
简言之,这个办法给了我们操作的空间,使得我们有了构造分段函数的可能。更本质的,使得我们有了构造条件语句的可能。
所以在这个测试点中,我们要从 �(�+∞)S(+∞x) 着手构造 ∣�∣∣x∣ (�(�+∞)S(+∞x) 这种写法不规范,但有助于理解)。
现在,再来考虑,如何将 �x 的正负区分开来。我们只有找到区分正负的办法,才可能构造出函数来模拟正负有别的 ∣�∣∣x∣ 函数。
区分正负的办法上面已经提到了,就是 �(�)S(x) 在正负无穷大处的两个极限,分别为 0,10,1 。
那么 �(−�)S(−x) 的极限就分别为 1,01,0 。
我们要想办法让这两个截然不同的极限对我们构造的函数产生影响,使得我们构造的函数在 �x 正负符号不同时具有显著的差别。
设这个影响为 �t ,把这个影响加到 −�+∞+∞−x 上去(这就是对我们构造的函数产生影响的操作过程)。现在考虑 �(−�+∞+�)S(+∞−x+t) 。
我们需要让这个影响在 �>0x>0 时为无穷小(即:几乎没什么影响),在 �<0x<0 时足够大,大到能显著影响 �(−�+∞+�)S(+∞−x+t) 的值。
所谓显著影响 �(−�+∞+�)S(+∞−x+t) 的值,无非就是把 �(−�+∞)S(+∞−x) 的值从 1221 附近变成 11 ,就是说 �(−�+∞+�)→1S(+∞−x+t)→1 。而减去 1221 再乘 44 后,这个影响作用的结果就变成了“使 00 变成 22 ”。
这说明 �t 应该是个由 11 搞出来的无穷大。比方说 1×2641×264 (这里未必就是 6464 这个数,还可以更大,而且这里的 11 不是确切的数字 11 ,它只是表示一个趋近于 11 但永远不等于 11 的变量)。
我们把这个大小为 22 的影响稍微调整一下,通过位移调整到和原来的影响 �t 大小相当的地步。这样,我们就可以通过减去 �t 来消除多余的影响,来构造出一个在 �<0x<0 时取 00 ,�>0x>0 时取 �x 的函数。
即 {0,�<0�,�>0{0,x<0x,x>0 。
这下就好办了。让这个函数乘 22 ,再减去 �x ,就得到 ∣�∣∣x∣ 啦!
上面的思考太抽象了,我们来重新整理一下思路:
-
首先,计算 �=�(−�×2�)×2�={0 ,�>02�,�<0t=S(−x×2q)×2p={0 ,x>02p,x<0 ,
��.PS. 这是 �=�(�×241)×2178y=S(x×241)×2178 的图像:
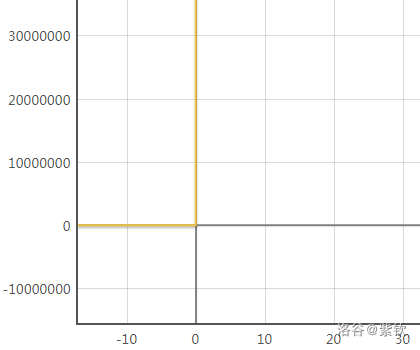
这里就要求 �(−�×2�)S(−x×2q) 能够与 00 或 11 近似相等,
-
于是令 �=−10−9x=−10−9 ,
只需有 11+�−2�10−9>1−10−901+e−2q10−91>1−10−90 ,
利用上面的近似公式,可知 1−�−2�10−9<11+�−2�10−91−e−2q10−9<1+e−2q10−91 ,
只需要 1−�−2�10−9>1−10−901−e−2q10−9>1−10−90 ,
即 2�10−9>90ln102q10−9>90ln10 ,
即 �>log2(9×1010ln10)≈37.59q>log2(9×1010ln10)≈37.59 ,
所以 �⩾38q⩾38 。
-
再令 �=10−9x=10−9 ,
只需有 11+�2�10−9<10−901+e2q10−91<10−90 ,
即 �2�10−9>1090−1e2q10−9>1090−1 ,
只需 �2�10−9>1090e2q10−9>1090 ,
即 2�10−9>90ln102q10−9>90ln10 ,与上种情况同解,
所以 �⩾38q⩾38 。
这样,在跳蚤看来,�(−�×2�)S(−x×2q) 与 00 或 11 是精确相等的。
��.PS. 这是 �=�(�×241)y=S(x×241) 的图像:
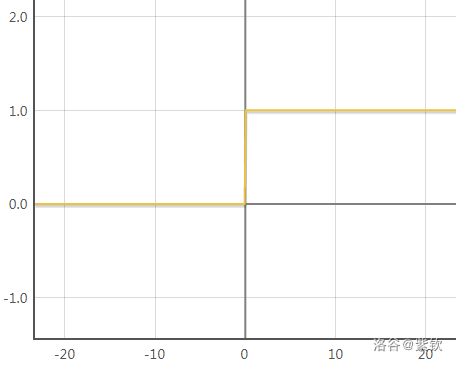
-
-
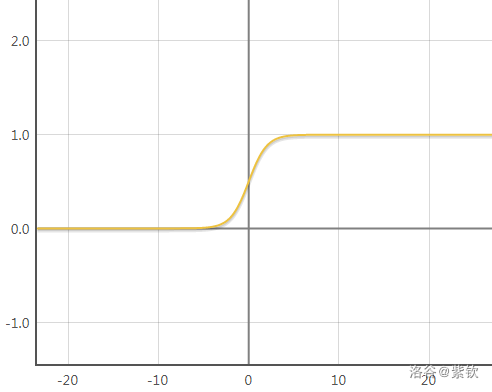
然后,计算 �(−�2�+�)={14−�2�+12,�>01 ,�<0S(2k−x+t)=⎩⎪⎪⎨⎪⎪⎧412k−x+21,x>01 ,x<0 ,
声明:为了方便书写,以下所有表达式 �x 均表示取反后的 �x ,但表达式中表示条件的 �x 仍然为未取反的 �x 。
声明:为了方便书写,以下所有表达式 �x 均表示取反后的 �x ,但表达式中表示条件的 �x 仍然为未取反的 �x 。
声明:为了方便书写,以下所有表达式 �x 均表示取反后的 �x ,但表达式中表示条件的 �x 仍然为未取反的 �x 。
-
这里要求 �>0x>0 时, (14�2�+12)−�(�2�)<10−90(412kx+21)−S(2kx)<10−90 ,不妨取 �=109x=109 ,即 1094×2�+12−11+�−2−�109<10−904×2k109+21−1+e−2−k1091<10−90
为了方便书写,设 1092�=�2k109=t ,
则上式为 �4+12−11+�−�<10−904t+21−1+e−t1<10−90
即 �4−1−�−�2(1+�−�)<10−904t−2(1+e−t)1−e−t<10−90 ,
即 �2−��−1��+1<2×10−902t−et+1et−1<2×10−90 ,
因为 �>0t>0 时, ��−1��+1>���+1et+1et−1>et+1t ,
这里用到了不等式 ��>�+1et>t+1 ,该不等式可用导数的相关知识来证明。
所以只需 �2−���+1<2×10−902t−et+1t<2×10−90 ,
即 ���−12(��+1)<2×10−90t2(et+1)et−1<2×10−90 ,
因为 �>0t>0 时, 1(��+1)<12(et+1)1<21 ,
所以只需 �(��−1)4<2×10−904t(et−1)<2×10−90 ,即 �(��−1)<8×10−90t(et−1)<8×10−90 ,
还是利用 ��>�+1et>t+1 ,欲使上式成立,至少需要满足 (��−1)2<8×10−90(et−1)2<8×10−90 ,
解得 �<ln(22×10−45+1)t<ln(22×10−45+1) ,
(其实只是个必要条件)
把 �=1092�t=2k109 代入,得 1092�<ln(22×10−45+1)2k109<ln(22×10−45+1) ,
即 2�>109ln(22×10−45+1)2k>ln(22×10−45+1)109 ,
即 �>9log210−log2(ln(22×10−45+1))≈177.884k>9log210−log2(ln(22×10−45+1))≈177.884 ,
所以 �⩾178k⩾178 。
当然 �k 不能取太大,否则会造成 �2�2kx 的精度下降,只需 10−9>2�×10−9010−9>2k×10−90 ,解得 �⩽269k⩽269 。
而且,我所采用的放缩方式,其放缩幅度还是很大的,所以 178178 的下界很松。但上界 269269 是严格的。
-
这里还要求 �<0x<0 时, 11+�−2�>1−10−901+e−2p1>1−10−90 ,
只需 1−�−2�>1−10−901−e−2p>1−10−90 ,
即 �>log2(90ln10)≈7.695p>log2(90ln10)≈7.695 ,
至于 �2�2kx ,它很小,只要 2�2p 够大,它对 2�2p 的影响就不足以改变 �(�2�+�)S(2kx+t) 的值。
所以 �⩾8p⩾8 。
-
其实没必要要求计算所得的数在 9090 位小数内精确相等,只要保证计算结果的 99 位小数是正确的,就能解决





 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 425
425

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








