C++算法笔记①

最新推荐文章于 2025-12-22 20:10:38 发布

原创最新推荐文章于 2025-12-22 20:10:38 发布 · 440 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #算法 #笔记

C++算法专栏收录该内容

4 篇文章

订阅专栏

该博客是C++算法笔记，涵盖NOI考点，如进制转换、图论、DP等算法知识，介绍了排列组合、杨辉三角等数学概念，还提及取值区间、随机数等内容。此外，详细阐述了骗分技巧，包括模拟、DFS、猜测答案等方法，并给出实战演练示例。

C++算法笔记①

NOI考点

NOI大纲(2023修订)

NOI笔试题库(2023)

进制转换

C++

十进制转k进制

#include<cstdio>
int main()
{
	char a[1000];
	int y=0,k,n,x;
	char z='A';
	scanf("%d%d",&n,&x);
	while(n!=0)
	{
		y++;
		a[y]=n%x;
		n=n/x;
		if(a[y]>9) a[y]+=z-10;
		else a[y]+='0';
	}
	for(int i=y;i>0;i--)
		printf("%c",a[i]);
	return 0;
}
m进制转10进制
#include<cstdio>
#include<cstring>
char a[10000];
int main()
{
	int n,m;
	int f=0;
	scanf("%s%d",a,&m);
	for(int i=0;i<strlen(a);i++)
	{
		f*=m;
		if (a[i]=='A'||a[i]=='B'||a[i]=='C'||a[i]=='D'||a[i]=='E'||a[i]=='F')
			f+=(a[i]-'A'+10);
		else
			f+=(a[i]-'0');
	}
	printf("%d",f);
	return 0;
}

注：用C语言的格式化输入输出可以快速转换10进制，8进制和16进制。

例子：10进制转16进制：

#include <cstdio>

int main()
{
	int a;
	scanf("%d",&a);
	printf("%x",a);
	return 0;
}

图论

1.数据元素称为顶点。

2.图是由顶点的有穷非空集合和顶点之间边的集合组成，表示为 $G = （ V ， E ）$ 。 $G$ 表示一个图， $V$ 是顶点的集合， $E$ 是顶点之间边的集合。

3.如果图的任意两个顶点之间的边都是无向边，则称该图为无向图，否则为有向图。

4.边上带权的图称为带权图或网图。

度：指依附于该顶点的边的个数。
重要公式：在具有n个顶点e条边的无向图中，度数之和等于边数的两倍。

5.入度之和等于出度之和等于 $e$ 。

6.无向完全图：如果任意两个顶点之间都存在边，则称该图为无向完全图。

7.含有 $n$ 个顶点的无向完全图有 $n * （ n - 1 ） /2$ 条边。

8.有向完全图：在有向图中，如果任意两顶点之间都存在方向互为相反的两条弧，则称为有向完全图。

9.含有 $n$ 个顶点的有向完全图有 $n * （ n - 1 ）$ 条边

路径的长度：路径上边的数目。
第一个顶点和最后一个顶点相同的路径称为回路。

10.简单路径：在路径序列中，顶点不重复出现的路径称为简单路径。

11.简单回路：除了第一个顶点和最后一个顶点之外，其余顶点不重复出现的回路称为简单回路。

12.通常情况下，路径指的都是简单路径，回路指的都是简单回路。

13.连通图：在无向图中，如果顶点 $v i$ 和 $v j$ 之间存在路径，则称 $v i$ 和 $v j$ 是连通的。若任意顶点 $v i$ 和 $v j$ 之间均有路径，则称该图是连通图。

14.非连通图的极大连通子图称为连通分量。

15.在有向图中，对任意顶点 $v i$ 和 $v j$ ，若从顶点 $v i$ 到 $v j$ 均有路径，则称该图是强连通图。

16.非强连通图的极大强连通子图称为强连通分量。

无向图的邻接矩阵一定是对称矩阵，而有向图的邻接矩阵不一定对称。

深度优先搜索

图的深度优先遍历类似于树的先序遍历。从图中某个顶点 $Vi$ 出发，访问此顶点并作已访问标记，然后从Vi的一个未被访问过的邻接点 $Vj$ 出发再进行深度优先遍历，当 $Vi$ 的所有邻接点都被访问过时，则退回到上一个顶点 $Vk$ ，再从 $Vk$ 的另一个未被访问过的邻接点出发进行深度优先遍历，直至图中所有顶点都被访问到为止。

对下图进行深度优先搜索，写出搜索结果。注意：从 $A$ 出发。
在这里插入图片描述

广度优先搜索（宽度优先搜索）

类似于树的按层次遍历。从图中某个顶点 $V 0$ 出发，访问此顶点，然后依次访问与 $V 0$ 邻接的、未被访问过的所有顶点，然后再分别从这些顶点出发进行广度优先遍历，直到图中所有被访问过的顶点的相邻顶点都被访问到。若此时图中还有顶点尚未被访问，则另选图中一个未被访问过的顶点作为起点，重复上述过程，直到图中所有顶点都被访问到为止。

对下图从A出发进行宽度优先搜索，写出搜索结果。

在这里插入图片描述

邻接矩阵

图的深度优先遍历

void DFS(int v) {
    cout << vertex[v];
    visited[v] = 1;
    for (int j = 0; j < vertexNum; j++) {
        if (edge[v][j] == 1 && visited[j] == 0) {
            DFS(j);
        }
    }
}

图的广度优先遍历

void BFS(int v) {
    int w, j, Q[MaxSize];
    int front = -1, rear = -1;
    cout << vertex[v];
    visited[v] = 1;
    Q[++rear] = v;
    while (front != rear) {
        w = Q[++front];
        for (j = 0; j < vertexNum; j++) {
            if (edge[w][j] == 1 && visited[j] == 0) {
                cout << vertex[j];
                visited[j] == 1;
                Q[++rear] = j;
            }
        }
    }
}

邻接表

实现方法

vector<int> G[MAX_V];
int main(){
	int V,E;
	scanf("%d %d",&V, &E);
	for(int i=0;i<E;i++){
		//从s向t连边
		int s,t;
		scanf("%d %d",&s,&t);
		G[s].push_back(t);
		//如果是无向图，则需要再从t向s连边
	}
	return 0;
}

图的深度优先遍历

void dfs(int v) {
    int j;
    EdgeNode* p = NULL;
    cout << adjlist[v].vertex;
    visited[v] = 1;
    p = adjlist[v].firstEdge;
    while (p != NULL) {
        j = p->adjvex;
        if (adjvex[j] == 0) {
            DFS2(j);
        }
        p = p->next;
    }
}

图的广度优先遍历

void bfs(int v) {
    int w, j, Q[MaxSzie];
    int front = -1;
    int rear = -1;
    EdgeNode* p = NULL;
    cout << adjlist[v].vertex;
    visited[v] = 1;
    Q[++rear] = v;
    while (front != rear) {
        w = Q[++front];
        p = adjlist[w].first;
        while (p != NULL) {
            j = p->adjvex;
            if (visited[j] == 0) {
                cout << adjlist[j].vertex;
                visited[j] = 1;
                Q[++rear] = j;
            }
            p = p->next;
        }
    }
}

前向星邻接表（链式前向星）

定义：

struct edge{
	int to,nt;     //to是边的终点，nt(next)是下一条边的序号
} e[边的数量];

int h[N],cnt;      // h[i]表示i的第一条在e里面序号，cnt是边的总数

建边：

inline void add(int a,int b){
	e[++cnt].to=b; 
	e[cnt].nt=h[a]; 
	h[a]=cnt;
}

读入：

while(m--) {
	int x,y;
	scanf("%d%d",&x,&y);
	add(x,y);
	add(y,x);
}

枚举与x的相邻的所有点：

for(int i=h[x]; i; i=e[i].nt) cout<<e[i].to;

整合：

struct edge{
	int to,nt; 
} e[边的数量];

int h[N],cnt;

void add(int a,int b) {
	e[++cnt].to=b;
	e[cnt].nt=h[a];
	h[a]=cnt;
}

int main() {
	while (m--) {
		int x,y;
		scanf(“%d%d”,&x,&y);

图的最短路径算法

分类：

多源最短路径算法：求任意两点之间的最短距离。
Floyd算法

单源最短路径算法：求一个点到其他所有点的最短路径
Dijkstra算法，Spfa算法，Bellman-ford算法

Floyd算法

时间复杂度 $O(n^3)$
本质上是一个动态规划
$f [i] [j]$ 表示 $i$ 到 $j$ 最短路径长度
开始的时候，如果i到j有边，那么f[i][j]就是直接的边长，如果没边, $f [i] [j]$ 就是无穷大。

for(int k=1; k<=n; k++) 
	for(int i=1; i<=n; i++) 
		for(int j=1; j<=n; j++)
			f[i][j]=min(f[i][j],f[i][k]+f[k][j]);

为什么k循环要写在最外面？

这个状态数组本来是3维的。
f[i][j][0]表示i到j的最短路径中间经过了 $0$ 个点。
$f [i] [j] [0] = e d g e [i] [j]$ , $e d g e [i] [j]$ 表示 $i$ 到 $j$ 直接的边长
如果i到j边不存在， $f [i] [j] [0]$ =无穷大。
f[i][j][k]表示i到j的最短路径中间最多经过了1到k这些点
答案就是 $f [i] [j] [n]$
$f [i] [j] [k] = min (一定没有经过 k, 一定经过 k) = min (f [i] [j] [k - 1], f [i] [k] [k - 1] + f [k] [j] [k - 1])$
把一维舍掉：
$f [i] [j] = min (f [i] [j], f [i] [k] + f [k] [j]);$

Dijkstra算法

思想 ：贪心的思想
步骤：
	1 标记所有的点都没有求得最短路径，所有的d[i]=无穷大，除了起点的d值是0。
	2 循环n次，每次从没有求得最短路径的点里面找出一个d值最小的点，把他标记，用这个点去更新其他没有求得最短路径的点。

void dijkstra() {
	memset(vis,0,sizeof(vis));
	for(int i=1;i<=n;i++) d[i]=inf;
	d[s]=0;
	for(int i=1;i<=n;i++) {
		int k=-1;
		for(int j=1;j<=n;j++)
			if(!vis[j] && (k==-1 || d[k]>d[j])) k=j;
		vis[k]=1;
		for(int j=1;j<=n;j++)
			if(!vis[j] && d[k]+edge[k][j]<d[j])
				d[j]=d[k]+edge[k][j];
	}
}

Spfa算法

设 $d i s t$ 代表 $s$ 到 $i$ 点的当前最短距离， $f a$ 代表 $s$ 到 $i$ 的当前最短路径中i点之前的一个点的编号。开始时 $d i s t$ 全部为 $+ \infty$ ，只有 $d i s t [s] = 0$ ， $f a$ 全部为 $0$ 。
维护一个队列，里面存放所有需要进行迭代的点。初始时队列中只有一个点 $S$ 。用一个布尔数组记录每个点是否处在队列中。
每次迭代，取出队头的点 $v$ ，依次枚举从 $v$ 出发的边 $v - > u$ ，设边的长度为 $l e n$ ，判断 $d i s t [v] + l e n$ 是否小于 $d i s t [u]$ ，若小于则改进 $d i s t [u]$ ，将 $f a [u]$ 记为 $v$ ，并且由于 $s$ 到 $u$ 的最短距离变小了，有可能u可以改进其它的点，所以若 $u$ 不在队列中，就将它放入队尾。这样一直迭代下去直到队列变空，也就是 $S$ 到所有的最短距离都确定下来，结束算法。

int const oo=1e9;
vector<int> a[N],b[N];
queue<int> q;
int s,t;
int v[N],d[N];

int spfa() {
	for(int i=1; i<=n; i++) d[i]=oo;
	q.push(s);
	v[s]=1;
	d[s]=0;
	while(!q.empty()) {
		int x=q.front();
		q.pop();
		v[x]=0;
		for(int i=0; i<a[x].size(); i++) {
			int tp=a[x][i];
			if(d[tp]>d[x]+b[x][i]) {
				d[tp]=d[x]+b[x][i];
				if(!v[tp]) {
					q.push(tp);
					v[tp]=1;
				}
			}
		}
	}
	if(d[t]==oo) d[t]=-1;
	return d[t];
}

DP

0-1背包问题（二维dp）
0-1背包升级版（二维dp）
完全背包（费解）如凑领钱（一维、二维dp）
子序列问题（重要）
    最长递增子序列（一维dp）
    最长公共子序列（二维dp）
    最长回文子序列（二维dp）
    最短编辑距离（二维dp）
最短路径（机器人走路）（二维dp）

第一步要明确两点，「状态」和「选择」。明确dp数组的定义

状态有两个：「背包的容量」、「可选择的物品」

选择有两个：「装进背包」、「不装进背包」
几种状态就是几层for循环，也就是几维dp
第二步，根据「选择」，思考状态转移的逻辑
第三步，确定初始条件

例题一：0-1背包升级版

给你一个可装载重量为W的背包和N个物品，每个物品有重量和价值两个属性。其中第i个物品的重量为wt[i]，价值为val[i]，现在让你用这个背包装物品，最多能装的价值是多少？

定义二维dp[i][j]：对于前i种物品，当前背包重量为j时，能够获得的最大价值为dp[i][j]。我们要求的就是dp[n][w]
数组元素之间的关系：
    当j - wt[i - 1] < 0 时：dp[i][j] = dp[i - 1][j]。表示当前剩余的容量装不下当前的物品，只能继承上一个装填的
    当j - wt[i - 1] >= 0 时：装或者不装。dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - wt[i - 1]] + val[i - 1])
数组元素之间的关系：dp[i] = dp[i - 1] + dp[i - 2]
初始条件：dp[...][0] = 0;dp[0][...] = 0。表示物品或者容量为0时，当前价值为0

// 经典动态规划：0-1背包问题
int baseDP(int w, int n, int weight[], int value[]){
    // 定义二维状态数组
    int dp[n + 1][w + 1];
    // 初始化边界
    for(int i = 0; i <= n; i++)
        dp[i][0] = 0;
    for(int i = 0; i <= w; i++)
        dp[0][i] = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= w; j++){
            if(j - weight[i - 1] < 0)
                // 装不下，直接继承前一个状态的
                dp[i][j] = dp[i - 1][j];
            // dp[i][j] = 择优（选择1， 选择2）
            // 背包装或者不装，两者择优选择
            else
                // 这个地方如果是一维数组的话就是倒着来的
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
        }
    }
    return dp[n][w];
}

例题二：0-1背包变体

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意：每个数组中的元素不会超过 100；数组的大小不会超过 200
示例 1:

输入: [1, 5, 11, 5]

输出: true

解释: 数组可以分割成 [1, 5, 5] 和 [11].

**定义dp[i][j]：对于前i个物品，当前背包的容量为j时，若dp[i][j]为true，则说明可以装满。我们要求的就是dp[N][sum/2] **
数组元素之间的关系：
    当j - wt[i - 1] < 0 时：dp[i][j] = dp[i - 1][j]。表示当前剩余的容量装不下当前的物品，只能继承上一个装填的
    当j - wt[i - 1] >= 0 时：dp[i][j] = dp[i - 1][j] || dp[i - 1][j - wt[i - 1]]
初始条件：初始条件：dp[...][0] = true;dp[0][...] = false。表示物品为0，价值不为0时，肯定装不满

class Solution {
public:

    bool ans = false;
	// 这种方法超时
    void dfs(vector<int> &num, vector<int> a, vector<int> b, int index){
        if(index == num.size()){
            int sumA = 0, sumB = 0;
            for(int i = 0; i < a.size(); i++)
                sumA += a[i];
            for(int i = 0; i < b.size(); i++)
                sumB += b[i];
            if(sumA == sumB)
                ans = true;
            return ;
        }
        // 放入A背包
        a.push_back(num[index]);
        dfs(num, a, b, index + 1);
        a.pop_back();
        b.push_back(num[index]);
        dfs(num, a, b, index + 1);
        b.pop_back();
    }

    bool canPartition(vector<int>& nums) {
        // 定义状态数组
        int sum = 0;
        for(int i : nums)
            sum += i;
        if(sum % 2 != 0)
            return false;
        int n = nums.size();
        sum = sum / 2;
        bool dp[n + 1][sum + 1];
        // 初始化
        for(int i = 0; i <= n; i++)
            dp[i][0] = true;
        for(int i = 0; i <= sum; i++)
            dp[0][i] = false;
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= sum; j++){
                if(j - nums[i - 1] < 0)
                    dp[i][j] = dp[i - 1][j];
                else
                    // 这个地方如果是一维数组的话就是倒着来的
                    dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];
            }
        }
        return dp[n][sum];
    }
};

例题三：完全背包问题

凑领钱1：给你k种面值的硬币，面值分别为c1, c2 ... ck，每种硬币的数量无限，再给一个总金额amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。

定义一维数组dp[i]：当前总金额为i时，需要最少dp[i]个硬币凑出这个金额。我们要求的就是dp[amount]
数组元素之间的关系：dp[i] = min(dp[i - coin] + 1)
初始条件：dp[0] = 0。即金额为0就需要0枚硬币

int coinChangeDP(vector<int> &coins, int amount){
    // 初始化备忘录
    vector<int> dp(amount + 1, amount + 1);
    dp[0] = 0;
    // 填表
    for(int i = 1; i < dp.size(); i++){
        // 内层循环，找最小
        for(int coin : coins){
            if(i - coin < 0)
                continue;
            dp[i] = min(dp[i], dp[i - coin] + 1);
        }
    }
    return (dp[amount] == amount + 1) ? -1 : dp[amount];
}

凑领钱2：给定不同面额的硬币和一个总金额，写出函数来计算可以凑成总金额的硬币组合数，假设每种面额的硬币有无限个。

定义二维数组dp[i][j]：当前总金额为j时，前i个物品可能有dp[i][j]种可能凑齐。我们要求的就是dp[n][amount]
数组元素之间的关系：
    当j-coins[i - 1] < 0时：dp[i][j] = dp[i - 1][j]。表示当前容量装不下当前的硬币，只能继承上一个状态的
    当j-coins[i - 1] >= 0时：dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]]
初始条件：dp[i][0] = 1;dp[0][i] = 0;

int change(int amount, vector<int>& coins) {

    if(amount == 0 && coins.size() == 0)
        return 1;

    int n = coins.size();
    int dp[n + 1][amount + 1];
    // 初始化
    for(int i = 0; i <= n; i++)
        dp[i][0] = 1;
    for(int i = 0; i <= amount; i++)
        dp[0][i] = 0;

    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= amount; j++){
            if(j - coins[i - 1] < 0)
                dp[i][j] = dp[i - 1][j];
            else
                // 注意这里是i不是i-1了，这样就保证了物品可以选无数次，如果是i-1的话，就是普通背包，只能选一次
                // 这个地方如果用一维数组，那么就是顺着来的
                dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i - 1]];
        }
    }
    
    return dp[n][amount];
}

例题四：最长公共子序列

解决两个字符串的动态规划问题，一般都是用两个指针i,j分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模。都是建立一个二维的dp数组。

求两个字符串的 LCS 长度：

输入: str1 = "abcde", str2 = "ace" 
输出: 3  
解释: 最长公共子序列是 "ace"，它的长度是 3

定义二维dp[i][j]：表示str1的(0, i)子序列与str2的(0, j)子序列的最长公共序列。我们要求的就是dp[m][n]
数组元素之间的关系：
    当str1[i] = str2[j]时：dp[i][j] = dp[i - 1][j - 1] + 1
    当str1[i] != str2[j]时：dp[i][j] = max(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1])
初始条件：dp[...][0] = dp[0][...] = 0

int myMax(int a, int b, int c){
    return max(max(a, b), c);
}

int longestComStr(string s1, string s2){
    int m = s1.size(), n = s2.size();
    int dp[m + 1][n + 1];
    // 初始化
    for(int i = 0; i <= m; i++)
        dp[i][0] = 0;
    for(int i = 0; i <= n; i++)
        dp[0][i] = 0;
    for(int i = 1; i <= m; i++){
        for(int j = 1; j <= n; j++){
            if(s1[i - 1] == s2[j - 1])
                dp[i][j] = dp[i - 1][j - 1] + 1;
            else
                // 这个地方写成dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])就行了
                dp[i][j] = myMax(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]);
        }
    }
    return dp[m][n];
}

例题五：求两个字符串的最小编辑距离

和上一个题一样，一般来说，处理两个字符串的动态规划问题，都是按本文的思路处理，建立 DP table。为什么呢，因为易于找出状态转移的关系。这里的dp(i)(j)数组表示的是 s1[0…i] 和 s2[0…j] 的最小编辑距离。

定义二维数组dp[i][j]：当字符串s1长度为i，字符串s2长度为j时，它们的最短编辑距离是dp[i][j]
数组元素之间的关系：
    当s1[i - 1] == s2[j - 1]时：dp[i][j] = dp[i - 1][j - 1]
    当s1[i - 1] != s2[j - 1]时：dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
初始条件：dp[i][0] = i;dp[0][i] = i

int min(int a, int b, int c){
    return min(min(a, b), c);
}

int minDistance(string s1, string s2){
    int m = s1.size(), n = s2.size();
    int dp[m + 1][n + 1];
    // 初始化
    for(int i = 0; i <= m; i++)
        dp[i][0] = i;
    for(int i = 0; i <= n; i++)
        dp[0][i] = i;
    for(int i = 1; i <= m; i++){
        for(int j = 1;j <= n; j++){
            if(s1[i - 1] == s2[j - 1])
                dp[i][j] = dp[i - 1][j - 1];
            else{
                dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);
            }
        }
    }
    // 储存着整个s1和s2的最小编辑距离
    return dp[m][n];
}

总结子序列问题模板

首先注意区分一个问题：

子序列：可以不连续的子字符串/子数组
子串：必须是连续的子字符串/子数组

遇到子序列问题，首先想到两种动态规划思路，然后根据实际问题看看哪种思路容易找到状态转移关系。

这类问题都是让你求一个最长子序列，因为最短子序列就是一个字符嘛，没啥可问的。一旦涉及到子序列和最值，那几乎可以肯定，考察的是动态规划技巧，时间复杂度一般都是 O(n^2)。
1 第一种思路模板是一维的 dp 数组

最长递增子序列（注意是序列，可以不连续）

定义一维dp[i]：数组中以num[i]结尾的最长递增序列为dp[i]。我们要求的就是所有的dp[i]中最大的那一个
数组元素之间的关系：dp[i] = max(dp[i], dp[j] + 1)，其中num[j] < num[i]
初始条件：dp[...] = 1，保证最短为1

int lengthOfLIS(int nums[], int n){

    vector<int> dp(n, 1);

    for(int i = 0; i < n; i++){
        for(int j = 0; j < i; j++){
            if(nums[j] < nums[i])
                dp[i] = max(dp[i], dp[j] + 1);
        }
    }

    int ans = INT_MIN;
    for(int i = 0; i < n; i++)
        ans = max(ans, dp[i]);

    return ans;
}

2 第二种思路模板是二维的 dp 数组

这种思路数组含义又分为「只涉及一个字符串」和「涉及两个字符串」两种情况

2.1 涉及两个字符串/数组时

最长公共子序列
最短编辑距离

2.2 涉及一个字符串/数组时

最长回文子序列（注意，和最长回文子串不一样，子序列可以不连续）

定义二维dp[i][j] 数组：在子串s[i..j]中，最长回文子序列的长度为dp[i][j]。我们要求的就是dp[0][n - 1]
数组元素之间的关系
    当s[i] = s[j]时：dp[i][j] = dp[i + 1][j - 1] + 2
    当s[i] != s[j]时：dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
初始条件：dp[i][i] = 1

为了保证每次计算dp[i][j]，左、下、左下三个方向的位置已经被计算出来，只能斜着遍历或者反着遍历，本例选择反着遍历：

// 反着遍历
int longestPalindromeSubseq(string s){
    int n = s.size();
    int dp[n][n];
    // 初始化
    memset(dp, 0, sizeof(dp));
    for(int i = 0; i < n; i++)
        dp[i][i] = 1;
    for(int i = n - 1; i >= 0; i--){
        for(int j = i + 1; j < n; j++){
            if(s[i] == s[j])
                dp[i][j] = dp[i + 1][j - 1] + 2;
            else
                dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
        }
    }
    // 返回整个s的最长回文子序列长度
    return dp[0][n - 1];
}

1 一维dp

例题一：青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个n级台阶总共有多少种跳法？

定义一维dp[i]：跳上一个i级的台阶共有dp[i]种跳法，我们要求的就是dp[n]
数组元素之间的关系：dp[i] = dp[i - 1] + dp[i - 2]
初始条件：dp[0] = 0;dp[1] = 1;dp[2] = 2

完整代码

// 跳台阶问题
// dp[n]表示跳上一个n阶台阶共有dp[n]种跳法
int f(int n){
    if(n <= 2)
        return n;
    int dp[n + 1];
    dp[0] = 0;
    dp[1] = 1;
    dp[2] = 2;
    for(int i = 3; i <= n; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[n];
}

2 二维dp

例题二：机器人走路（不含权值）

⼀个机器⼈位于⼀个 m x n ⽹格的左上⻆ （起始点在下图中标记为“Start” ）。
机器⼈每次只能向下或者向右移动⼀步。机器⼈试图达到⽹格的右下⻆（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

定义二维dp[i][j]：当机器人从左上角走到(i, j)这个位置，共有dp[i][j]种路径，我们要求的就是dp[m - 1][n - 1]
数组元素之间的关系：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
初始条件：dp[...][0] = 1;dp[0][...] = 1，因为第一行只能往左走，第一列只能往下走

完整代码

// 机器人走路(无路径权值)
// dp[i][j]表示当机器人从左上角走到(i,j)这个位置时，一共有dp[i][j]种路径
int f(int m, int n){
    if(m < 0 || n < 0)
        return 0;

    int dp[m][n];
    for(int i = 0; i < m; i++)
        dp[i][0] = 1;
    for(int i = 0; i < n; i++)
        dp[0][i] = 1;

    for(int i = 1; i < m; i++){
        for(int j = 1; j < n; j++)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
    }
    return dp[m - 1][n - 1];
}

例题三：机器人走路的最短路径（含权值）

给定⼀个包含⾮负整数的 m x n ⽹格，请找出⼀条从左上⻆到右下⻆的路径，使得路径上的数字总和为最⼩。

定义二维dp[i][j]：当机器人从左上角走到(i, j)这个位置的最短路径，我们要求的就是dp[m - 1][n - 1]
数组元素之间的关系：dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + val[i][j]
初始条件：dp[i][0] = dp[i - 1][0] + val[i][0];dp[0][i] = dp[0][i - 1] + val[0][i]

完整代码

// 机器人走路，有路径权值
// dp[i][j]表示机器人从左上角走到(i,j)这个位置的最短路径值
int f(int val[][], int m, int n){
    int dp[m][n];
    dp[0][0] = val[0][0];
    for(int i = 1; i < m; i++)
        dp[i][0] = dp[i - 1][0] + val[i][0];

    for(int i = 1; i < n; i++)
        dp[0][i] = dp[0][i - 1] + val[0][i - 1];

    for(int i = 1; i < m; i++){
        for(int j = 1; j < n; j++){
            dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + val[i][j];
        }
    }
    return dp[m - 1][n - 1];
}

例题四：最短编辑距离

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使⽤的最少操作数 。
你可以对⼀个单词进⾏如下三种操作：

插⼊⼀个字符 删除⼀个字符 替换⼀个字符

定义二维数组dp[i][j]：当字符串s1长度为i，字符串s2长度为j时，它们的最短编辑距离是dp[i][j]
数组元素之间的关系：
    当s1[i - 1] == s2[j - 1]时：dp[i][j] = dp[i - 1][j - 1]
    当s1[i - 1] != s2[j - 1]时：dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
初始条件：dp[i][0] = i;dp[0][i] = i

完整代码

int min(int a, int b, int c){
    return min(min(a, b), c);
}

int minDistance(string s1, string s2){
    int m = s1.size(), n = s2.size();
    int dp[m + 1][n + 1];
    // 初始化
    for(int i = 0; i <= m; i++)
        dp[i][0] = i;
    for(int i = 0; i <= n; i++)
        dp[0][i] = i;
    for(int i = 1; i <= m; i++){
        for(int j = 1;j <= n; j++){
            if(s1[i - 1] == s2[j - 1])
                dp[i][j] = dp[i - 1][j - 1];
            else{
                dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1);
            }
        }
    }
    // 储存着整个s1和s2的最小编辑距离
    return dp[m][n];
}

例题一：0-1背包问题

//weight:物品重量，n:物品个数，w:背包可承载重量
// 二维dp
public int knapsack(int[] weight, int n, int w) {
  boolean[][] states = new boolean[n][w+1]; // 默认值false
  states[0][0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
  if (weight[0] <= w) {
    states[0][weight[0]] = true;
  }
  for (int i = 1; i < n; ++i) { // 动态规划状态转移
    for (int j = 0; j <= w; ++j) {// 不把第i个物品放入背包
      if (states[i-1][j] == true) states[i][j] = states[i-1][j];
    }
    for (int j = 0; j <= w-weight[i]; ++j) {//把第i个物品放入背包
      if (states[i-1][j]==true) states[i][j+weight[i]] = true;
    }
  }
  for (int i = w; i >= 0; --i) { // 输出结果
    if (states[n-1][i] == true) return i;
  }
  return 0;
}

// 一维dp
public static int knapsack2(int[] items, int n, int w) {
  boolean[] states = new boolean[w+1]; // 默认值false
  states[0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
  if (items[0] <= w) {
    states[items[0]] = true;
  }
  for (int i = 1; i < n; ++i) { // 动态规划
    for (int j = w-items[i]; j >= 0; --j) {//把第i个物品放入背包
      if (states[j]==true) states[j+items[i]] = true;
    }
  }
  for (int i = w; i >= 0; --i) { // 输出结果
    if (states[i] == true) return i;
  }
  return 0;
}

排列组合

概念:

中心:

排列组合的中心问题是研究给定要求的排列和组合可能出现的情况总数。

排列:

就是指从给定个数的元素中取出指定个数的元素进行排序。

组合:

则是指从给定个数的元素中仅仅取出指定个数的元素，不考虑排序。

排列:

排列的定义:

从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；

从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m）表示。

其计算公式:

A(n,m)=n(n-1）（n-2）……（n-m+1）= n!/(n-m)! 此外规定0!=1

组合:

定义:

从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；

从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。

其计算公式:

C(n,m)= $A(n,m)^{2}$ /m!=A(n,m)/m！； C(n,m)=C(n,n-m）。（其中n≥m)

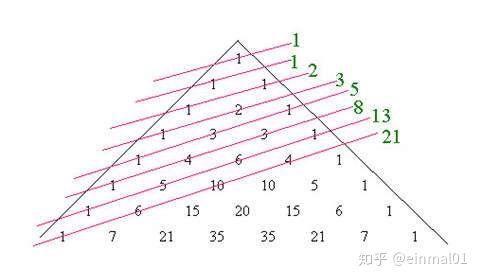
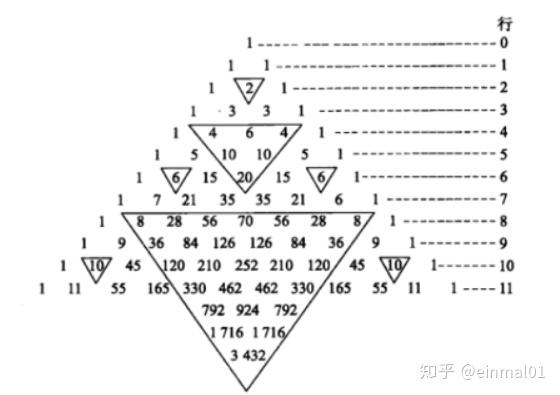
特别的，将组合展开，可以得到杨辉三角

其他:

1.从n个元素中取出m个元素的循环排列数=A(n,m)/m=n!/m(n-m)!.

2.n个元素被分成k类，每类的个数分别是n1,n2,…nk这n个元素的全排列数为 n!/(n1！×n2！×…×nk!).

3.k类元素，每类的个数无限，从中取出m个元素的组合数为C(m+k-1,m）。

杨辉三角

链接:

杨辉三角

百科

图形:

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 5 1

1 6 15 15 6 1

1 7 21 30 21 7 1

…

公式:

1.杨辉恒等式:

C(n,m)=C(n-1,m-1)+C(n-1,m)（n=1，2，3，···n）。

2.左右对称性:

C(n,r)=C(n,n-r)

3.个数与和:

第n行的数字有n项，数字和为2的n-1次幂。

4.黄金分割:

将杨辉三角按如下图所示划出斜线:

再求出斜线所经过的数字的和:

1,1,2,3,5,8,13,21,34,55,89…

此数列就是著名的斐波那契数列。这个数列最大特点就是其中每一项都等于其前两项的和。

从第三个数起,每个数与它后面那个数的比值，都很接近于0.618,正是"黄金分割比"。

5.奇偶图形:

将偶数与奇数分别标出，可以看到，所有偶数会以倒立的等边三角形排列，奇数都成正立的三角形排列。

且等边三角形(偶数)的边长依次为：

3,7,15,31,63,80,99,120…

即所有的偶数依次排出以 $2^{n}$ 为边长的倒立等边三角形。

将所有等边三角形中的偶数去掉，剩下的图形是一个类似于分形几何中的谢尔宾斯基三角形。

取值区间

假设 a,b 是两个实数,且 $a \leq b$ . 例如 $3 ， 8$

1.开区间

满足 a ＜ x ＜b 的实数 x 的集合, ————3 < x < 8 的实数x的集合
表示为 ( a,b ),叫做开区间;—————（ 3，8 ），不包括头，不包括尾

一般用（）表示

2.闭区间

满足 a ≤ x ≤ b 的实数 x 的集合,————3 ≤ x ≤ b的实数x的集合
表示为 [ a,b ],叫做闭区间;————[ 3, 8 ] ，包括头，包括尾

一般用 [ ] 表示

3.半开区间

满足 a ≤ x ＜b,a ＜x ≤ b 的实数 x 的集合,————3 ≤ x < 8， 3 < x ≤ 8的实数x的集合
分别表示为 [ a,b ),( a,b ],叫做半开区间.————

[ 3, 8 ) 右闭左开 包括头，不包括尾
( 3, 8 ] 左开右闭 不包括头，包括尾

这里实数 a,b 叫做区间的端点.

从上边的三个定义你就可以看出来,闭区间是有a,b两个端点的.

随机数

C++随机数

C++提供了两个函数，用于返回随机数：rand() 和 srand()
rand()

功能：随机数发生器

用法：

// #include<stdlib.h>
int rand(void)

rand()的内部实现是用线性同余法做的，简单的讲就是通过类似于一个数学周期函数去生成一个数字。而这个周期又特别的长，所以在一定范围内可以看成是随机的。故单独使用rand()生成的随机数实际上是伪随机数。

当用户未设定随机数种子时，系统会默认随机数种子为1。随机数种子可以简单地理解成上面提到的数学周期函数的参数。

因为rand() 产生的是伪随机数字，每次执行时是相同的“周期函数”; 若要不同, 可以用函数 srand() 初始化它。换个简单的理解方式：srand()就是给“周期函数”添加了一个参数。
srand()

功能：

初始化随机数发生器

用法：

// #include<stdlib.h>
void srand(unsigned int seed)
    
/*
unsigned：无符号
表示抛弃数据类型的负数部分，将更多的存储空间用来存放非负数
例如：int类型原本占用4字节空间，即只能存储[-2^31,2^31 - 1]范围内的数据
加unsigned后存储数据的范围就是[0,2^32 - 1]

unsigned int表示[0,2^32 - 1]范围内的整型
*/

srand() 用来设置 rand() 产生随机数时的随机数种子。参数 seed 必须是个整数，如果每次 seed 都设相同值，rand() 所产生的随机数值每次就会一样。所以想要生成指定数量的随机数，就需要在每次使用rand()都使用srand()重新产生一个随机数种子。
使用time()作为随机数种子

功能：

时间戳，返回从1970年1月1月零点零分零秒到当前时间的秒数

用法：

// #include<time.h>
time_t time(time_t * t);    // 指针t用于存放返回的时间，可以传空指针

我们可以将time返回的时间作为参数传递给srand()，因为程序每一次运行时，我们的时间都是不一样的，即每次运行时的随机数种子都不一样。

srand((unsigned)time(NULL));
rand();

随机数范围计算

首先我们可以通过rand() % n的方式，获取到[0,n)的随机数，因为任何一个数除以n得到的余数0到n-1。那么我们就可以通过改变n的值就可以去指定截止数，再将取到的范围加上一个值就可以改变起始数：

要取得 [a,b) 的随机整数，使用 (rand () % (b-a))+ a;
要取得 [a,b] 的随机整数，使用 (rand () % (b-a+1))+ a;
要取得 (a,b] 的随机整数，使用 (rand () % (b-a))+ a + 1;

要取得 0～1 之间的浮点数，可以使用 rand () /double (RAND_MAX)。

#include<iostream>
#include<stdlib.h>
#include<time.h>
using namespace std;

int main() {
    // 生成随机数种子
    srand((unsigned)time(NULL));
    
    // RAND_MAX 是 rand() 函数能够产生的最大随机数
    cout << "RAND_MAX:" << RAND_MAX << endl;
    
    int a = 1, b = 10;
    // 生成[a,b)的随机数
    cout << (rand() % (b-a)) + a << endl;
    
    // 生成[a,b]的随机数
    cout << (rand() % (b-a+1)) + a << endl;
    
     // 产生(a, b] 的随机数，可以使用(rand() % (b - a)) + a + 1;
 	cout << (rand() % (b - a)) + a + 1 << endl;
    
    // 产生[0, 1] 的浮点数，可以使用 rand() / double(RAND_MAX);
 	cout << rand() / double(RAND_MAX) << endl;
    
    return 0;
}

逆元

long long p = 998244353;
long long inv(long long a, long long b) { // a/b % 998244353
	if (b == 1) return a;
	return 1ll * inv(a, p % b) * (p - p / b) % p;
}

$inv_{i}=i^{-1}%m$

$inv_{i}=- \lfloor m/i \rfloor \times inv_{m \bmod i} \bmod m$

$inv_{1}=1$

骗分

$\huge\color{qwq}\texttt{骗分导论}$
$\color{Lime}\sf{THE\ NEW\ GUIDE\ OF\ CHEATING\ IN\ INFORMATICS\ OLYMPIAD.}$
$\color{DarkTurquoise}\texttt{蒟蒻的宝书}$

在Oier中，有一句话广为流传：
$\color{Aqua}\texttt{“ 任何蒟蒻必须经过大量的刷题练习才能成为大牛乃至于神牛 ”}$
这就是著名的lzn定理。然而，我们这些蒟蒻们，没有经过那么多历练，却要和大牛们同场竞技，我们该怎么以弱胜强呢？答案就是：骗分
那么，骗分是什么呢？骗分就是用简单的程序（比标准算法简单很多，保证蒟蒻能轻松搞定的程序），尽可能多得骗取分数。
让我们走进这篇《骗分导论》，来学习骗分的技巧，来挑战神牛吧！

第2章从无解出发

2.1 无解情况

在很多题目中都有这句话：
$\color{Aqua}\texttt{“ 若无解，请输出 -1。”}$
看到这句话时，骗分的蒟蒻们就欣喜若狂，因为——数据中必定会有无解的情况！那么，只要打出下面这句话：

printf("-1");

就能得到10分，甚至20分，30分！
举个例子：

NOIP2012第4题，文化之旅

题目描述 Description

有一位使者要游历各国，他每到一个国家，都能学到一种文化，但他不愿意学习任何一种文化超过一次（即如果他学习了某种文化，则他就不能到达其他有这种文化的国家）。不同的国家可能有相同的文化。不同文化的国家对其他文化的看法不同，有些文化会排斥外来文化（即如果他学习了某种文化，则他不能到达排斥这种文化的其他国家）。

现给定各个国家间的地理关系，各个国家的文化，每种文化对其他文化的看法，以及这位使者游历的起点和终点（在起点和终点也会学习当地的文化），国家间的道路距离，试求从起点到终点最少需走多少路。

输入描述 Input Description

第一行为五个整数N，K，M，S，T，每两个整数之间用一个空格隔开，依次代表国家个数（国家编号为1到N），文化种数（文化编号为1到K），道路的条数，以及起点和终点的编号（保证S不等于T）；

第二行为N个整数，每两个整数之间用一个空格隔开，其中第i个数Ci，表示国家i的文化为Ci。

接下来的K行，每行K个整数，每两个整数之间用一个空格隔开，记第i行的第j个数为aij，aij= 1表示文化i排斥外来文化j（i等于j时表示排斥相同文化的外来人），aij= 0表示不排斥（注意i排斥j并不保证j一定也排斥i）。

接下来的M行，每行三个整数u，v，d，每两个整数之间用一个空格隔开，表示国家u与国家v有一条距离为d的可双向通行的道路（保证u不等于v，两个国家之间可能有多条道路）。

输出描述 Output Description

输出只有一行，一个整数，表示使者从起点国家到达终点国家最少需要走的距离数，如果无解则输出-1

样例输入 Sample Input

输入样例1

2 2 1 1 2

1 2
0 1
1 0
1 2 10
输入样例2

2 2 1 1 2

1 2
0 1
0 0
1 2 10
样例输出 Sample Output

输出样例1

-1
输出样例2

10
数据范围及提示 Data Size & Hint

【输入输出样例1说明】

由于到国家2必须要经过国家1，而国家2的文明却排斥国家1的文明，所以不可能到达国家2。

【输入输出样例2说明】

路线为1 -> 2。

【数据范围】

对于20%的数据，有2≤N≤8，K≤5；

对于30%的数据，有2≤N≤10，K≤5；

对于50%的数据，有2≤N≤20，K≤8；

对于70%的数据，有2≤N≤100，K≤10；

对于100%的数据，有2≤N≤100，1≤K≤100，1≤M≤N2，1≤ki≤K，1≤u,v≤N，1≤d≤1000，S≠T，1 ≤S, T≤N。

这道题看起来很复杂，但其中有振奋人心的一句话 “输出-1” ，我考试时就高兴坏了（当时我才初一，水平太烂），随手打了个

printf("-1");

得10分。

2.2 样例——白送的分数

每道题目的后面，都有一组“样例输入”和“样例输出”。它们的价值极大，不仅能初步帮你检验程序的对错（特别坑的样例除外），而且，如果你不会做这道题（这种情况蒟蒻们已经司空见惯了），你就可以直接输出样例！
例如美国的USACO，它的题目有一个规则，就是第一组数据必须是样例。那么，只要你输出所有的样例，你就能得到100分（满分1000）！这是相当可观的分数了。
现在，你已经掌握了最基础的骗分技巧。只要你会基本的输入输出语句，你就能实现这些骗分方法。那么，如果你有一定的基础，请看下一章——我将教你怎样用简单方法骗取部分分数。

第3章 “艰苦朴素永不忘”

本章的标题来源于《学习雷锋好榜样》的一句歌词，但我不是想教导你们学习雷锋精神，而是学习骗分！
看到“朴素”两个字了吗？它们代表了一类算法，主要有模拟和DFS。下面我就来介绍它们在骗分中的应用。

3.1 模拟

所谓模拟，就是用计算机程序来模拟实际的事件。例如NOIP2012的“寻宝”，就是写一个程序来模拟小明上藏宝塔的动作。
较繁的模拟就不叫骗分了，我这里也不讨论这个问题。
模拟主要可以应用在骗高级数据结构题上的分，例如线段树。下面举一个例子来说明一下：

排  队(USACO 2007 January Silver)

【问题描述】

每天，农夫约翰的N（1≤N≤50000）头奶牛总是按同一顺序排好队，有一天，约翰决定让一些牛玩一场飞盘游戏（Ultimate Frisbee），他决定在队列里选择一群位置连续的奶牛进行比赛，为了避免比赛结果过于悬殊，要求挑出的奶牛身高不要相差太大。

约翰准备了Q（1≤Q≤200000）组奶牛选择，并告诉你所有奶牛的身高Hi（1≤  Hi ≤106）。他想知道每组里最高的奶牛和最矮的奶牛身高差是多少。

注意：在最大的数据上，输入输出将占据大部分时间。

【输入】

第一行，两个用空格隔开的整数N和Q。

第2到第N+1行，每行一个整数，第i+1行表示第i头奶牛的身高Hi

第N+2到第N+Q+1行，每行两个用空格隔开的整数A和B，表示选择从A到B的所有牛（1 ≤ A ≤ B ≤ N）

【输出】

共Q行，每行一个整数，代表每个询问的答案。

输入样例    输出样例

6 3
1
7
3
4
2
5
1 5
4 6
2 2         6

3
0

对于这个例子，大牛们可以写个线段树，而我们蒟蒻，就模拟吧。
附模拟程序：

for(int i=1;i&lt;=q;i++){
    scanf("%d%d",&amp;a,&amp;b);
    int min=INT_MAX,max=INT_MIN;
    for(int i=a;i&lt;=b;i++){
        if(h[i]&lt;min)min=h[i];
        if(h[i]&gt;max)max=h[i];
    }
    printf("%d\n",max-min);
}

程序简洁明了，并且能高效骗分。本程序得50分。

3.2 万能钥匙——DFS

DFS是图论中的重要算法，但我们看来，图论神马的都是浮云，关键就是如何骗分。下面引出本书的第2条定理：
$\color{Aqua}\texttt{“ DFS是万能的。”}$
这对于你的骗分是至关重要的。比如说，一些动态规划题，可以DFS；数学题，可以DFS；剪枝的题，更能DFS。下面以一道省选题为例，解释一下DFS骗分。

例题：NOIP2003，采药

题目描述 Description

辰辰是个天资聪颖的孩子，他的梦想是成为世界上最伟大的医师。为此，他想拜附近最有威望的医师为师。医师为了判断他的资质，给他出了一个难题。医师把他带到一个到处都是草药的山洞里对他说：“孩子，这个山洞里有一些不同的草药，采每一株都需要一些时间，每一株也有它自身的价值。我会给你一段时间，在这段时间里，你可以采到一些草药。如果你是一个聪明的孩子，你应该可以让采到的草药的总价值最大。”

如果你是辰辰，你能完成这个任务吗？

输入描述 Input Description

输入第一行有两个整数T（1<=T<=1000）和M（1<=M&<=100），用一个空格隔开，T代表总共能够用来采药的时间，M代表山洞里的草药的数目。接下来的M行每行包括两个在1到100之间（包括1和100）的整数，分别表示采摘某株草药的时间和这株草药的价值。

输出描述 Output Description

输出包括一行，这一行只包含一个整数，表示在规定的时间内，可以采到的草药的最大总价值。

样例输入 Sample Input

70 3
71 100
69 1
1 2
样例输出 Sample Output

3
数据范围及提示 Data Size & Hint

对于30%的数据，M<=10；

对于全部的数据，M<=100。

这题的方法很简单。我们瞄准20%的数据来做，可以用DFS枚举方案，然后模拟计算出最优解。附一个大致的代码：

void DFS(int d,int c){
    if(d==n){if(c&gt;ans)ans=c; return;}
    DFS(d+1,c+w[i]);
    DFS(d+1,c);
}

第4章骗分的关键——猜想

4.1 听天由命

如果你觉得你的人品很好，可以试试这一招——输出随机数。
先看一下代码：

#include<stdlib.h>
#include<time.h>
//以上两个头文件必须加
srand(time(NULL));
//输出随机数前执行此语句
printf("%d",rand()%X);
//输出一个0~X-1的随机整数。

这种方法适用于输出一个整数（或判断是否）的题目中，答案的范围越小越好。让老天决定你的得分吧。

据说，在NOIP2013中，有人最后一题不会，愤然打了个随机数，结果得了70分啊!!

4.2 猜测答案

有些时候，问题的答案可能很有特点：对于大多数情况，答案是一样的。这时，骗分就该出手了。你需要做的，就是发掘出这个答案，然后直接输出。

有时，你需要运用第3章中学到的知识，先写出朴素算法，然后造一些数据，可能就会发现规律。

例如，本班月赛中有一道题：

炸毁计划

【问题描述】

皇军侵占了通往招远的黄金要道。为了保护渤海通道的安全，使得黄金能够顺利地运送到敌后战略总指挥地延安，从而购买战需武器，所以我们要通过你的程序确定这条战略走廊是否安全。

已知我们有N座小岛，只有使得每一个小岛都能与其他任意一个小岛联通才能保证走廊的安全。每个小岛之间只能通过若干双向联通的桥保持联系，已知有M座桥(Ai,Bi)表示第i座桥连接了Ai与Bi这两座城市。

现在，敌人的炸药只能炸毁其中一座桥，请问在仅仅炸毁这一座桥的情况下，能否保证所有岛屿安全，都能联通起来。

现在给出Q个询问Ci，其中Ci表示桥梁编号，桥梁的编号按照输入顺序编号。每个询问表示在仅仅炸毁第Ci座桥的情况下能否保证所有岛屿安全。如果可以，在输出文件当中，对应输入顺序输出yes，否则输出no（输出为半角英文单词，区分大小写，默认为小写，不含任何小写符号，每行输出一个空格，忽略文末空格）。

【输入格式】

第一行 三个整数N，M，Q，分别表示岛屿的个数，桥梁的个数和询问的个数。

第二行到第M+1行 每行两个整数。第i+1行有两个整数Ai Bi表示这个桥梁的属性。

第M+2行 有Q个整数Ci表示查询。

【输出格式】

Q行，表示查询结果。

【样例】

destroy.in    destroy.out

2 1 1
1 2
1             no

【样例范围】

对于80%的数据，N≤100。

对于100%的数据，N≤1000，N,Q≤M≤2000 。

你发现问题了吗？那么多座桥，炸一座就破坏岛屿的联系，可能性微乎其微（除非特别设计数据）。那么，我们的骗分策略就出来了：对于所有询问，输出yes.果然，此算法效果不错，得80分。
现在知道猜测答案的厉害了吧？

4.3 寻找规律

首先声明：本节讲的规律不是正当的算法规律，而是数据的特点。

某些题目会给你很多样例，你就可以观察他们的特点了。有时，数据中的某一个（或几个）数，能通过简单的关系直接算出答案。

只要你找到了规律，在很多情况下你都能得到可观的分数。

这样的题目大多出现在NOI或更高等级的比赛中，本人蒟蒻一个，就不举例了。传说某人去省选时专门琢磨数据的规律，结果有一题得了30分。

4.4 小数据杀手——打表

我认识一个人，他在某老师家上C语言家教，老师每讲一题，他都喊一句：“打表行吗？”

他真的是打表的忠实粉丝。表虽然不能乱打，但还是很有用的。

先看一个例子：

NOIP2003 栈

题目描述 Description

栈是计算机中经典的数据结构，简单的说，栈就是限制在一端进行插入删除操作的线性表。

栈有两种最重要的操作，即pop（从栈顶弹出一个元素）和push（将一个元素进栈）。

栈的重要性不言自明，任何一门数据结构的课程都会介绍栈。宁宁同学在复习栈的基本概念时，想到了一个书上没有讲过的问题，而他自己无法给出答案，所以需要你的帮忙

宁宁考虑的是这样一个问题：一个操作数序列，从1，2，一直到n（图示为1到3的情况），栈A的深度大于n。

现在可以进行两种操作，

1.将一个数，从操作数序列的头端移到栈的头端（对应数据结构栈的push操作）

2. 将一个数，从栈的头端移到输出序列的尾端（对应数据结构栈的pop操作）

使用这两种操作，由一个操作数序列就可以得到一系列的输出序列，下图所示为由1 2 3生成序列2 3 1的过程。（原始状态如上图所示） 。

你的程序将对给定的n，计算并输出由操作数序列1，2，…，n经过操作可能得到的输出序列的总数。

输入描述 Input Description

输入文件只含一个整数n（1≤n≤18）

输出描述 Output Description

输出文件只有一行，即可能输出序列的总数目

样例输入 Sample Input

3
样例输出 Sample Output

5

这题看似复杂，但数据范围太小，N<=18。所以，骗分程序就好写了：

int a[18]={1,2,5,14,42,132,429,1430,4862,16796,58786,208012,742900,2674440,9694845,35357670,129644790,477638700};

scanf("%d",&amp;n);

printf("%d",ans[n-1]);

测试结果不言而喻，AC了。

学完这一章，你已基本掌握了骗分技巧。下面的内容涉及一点算法知识，难度有所增加。蒟蒻中的蒟蒻可以止步于此了。

第5章做贪心的人

5.1 贪心的算法

给你一堆纸币，让你挑一张，相信你一定会挑面值最大的。其实，这就是贪心算法。

贪心算法是个复杂的问题，但你不用管那么多。我们只关心骗分。给你一个问题，让你从一些东西中选出一些，你就可以使用贪心的方法，尽量挑好的。

举个例子：这是我们的市队选拔的一道题。

2. 有趣的问题

【问题描述】

2013 年的NOIP 结束后， Smart 发现自己又被题目碾压了，心里非常地不爽，于是

暗下决心疯狂地刷数学题目，做到天昏地暗、废寝忘食，准备在今年的中考中大展身手。

有一天，他在做题时发现了一个有趣的问题：

给定n 个二元组(ai, bi)，记函数：

y=100\*sigma(ai)/sigma(bi);

将函数y 的值四舍五入取整。

现将n 个二元组去掉其中的k 个计算一个新的y 值（也四舍五入取整），均能满足：y <= z ，求出最小的z值。Smart 想让你帮他一起找出最小的z值。

【输入格式】

输入包含多组测试数据。每组测试数据第一行两个整数：n和k；第二行为n 个数：

a1 a2 …… an；第三行为；n 个数： b1 b2 …… bn。

输入数据当n、k 均为0 时结束。

【输出格式】

对于每组测试数据输出一行，即找出的最小的冘值。

注意：为避免精度四舍五入出现误差，测试点保证每个函数值与最终结果的差值至少为0.001 。

【样例】

math.in

3 1
5 0 1
5 1 6
4 2
1 2 7 9

5 6 7 9

0 0
math. out

83
100
【数据范围】

对于40% 的数据： n≤20；

对于70% 的数据： n≤1000；

对于100% 的数据： n≤10000，ai,bi 都在int 范围内。

这题让人望而生畏，但我们有贪心的手段。每个二元组的a值是乘到答案中的，所以a越大越好，那么只要选择出最小的k个去掉即可。代码就不写了，因为这个设计到下一章的内容：排序。

此代码得20分。

5.2 贪心地得分

我们已经学了很多骗分方法，但他们中的大多效率并不高，一般能骗10~20分。这不能满足我们的贪心。

然而，我们可以合成骗分的程序。举个最简单的例子，有些含有无解情况的题目，它们同样有样例。我们可以写这个程序：

if(是样例) printf(样例);
else printf("-1");

这样也许能变10分为20分，甚至更多。

当然，合并骗分方法时要注意，不要重复骗同一种情况，或漏考虑一些情况。

大量能骗分的问题都能用此法，大家可以试试用新方法骗2.1中的例子 “文化之旅”。

第6章 C++的福利

$\color{Aqua}\texttt{请P党们跳过本章，这不是你们的福利。}$
在C++中，有一个好东西，名唤STL，被万千Oier们所崇拜，所喜爱。下面让我们走进STL。

6.1 快速排序

快速排序是一个经典算法，也是C++党的经典福利。他们有这样的代码：

#include<algorithm>//快速排序头文件
sort(a,a+n);//对一个下标从0开始存储，长度为n的数组升序排序

就这么简单，完成了P党一大堆代码干的事情。

6.2 “如意金箍棒”

C++里有一种东西，叫vector容器。它好比如意金箍棒，可以随着元素的数量而改变大小。它其实就是数组，却比数组强得多。

下面看看它的几种操作：

#include&lt;vector&gt;//vector头文件
vector&lt;int&gt; V;//定义
V.push_back(x);//末尾增加一个元素x
V.pop_back();//末尾删除一个元素
V.size();//返回容器中的元素个数

它同样可以使用下标访问。（从0开始）

第7章 “宁为玉碎，不为瓦全”

至此，我已介绍完了我所知的骗分方法。如果上面的方法都不奏效，我也无能为力。但是，我还有最后一招——

有句古话说：“宁为玉碎，不为瓦全”。我们蒟蒻也应有这样的精神。骗不到分，就报复一下，卡评测以泄愤吧！

卡评测主要有两种方法：一是死循环，故意超时；二是进入终端，卡住编译器。

先介绍下第一种。代码很简单，请看：

while(1);

就是这短短一句话，就能卡住评测机长达10s，20s，甚至更多！对于测试点多、时限长的题目，这是个不错的方法。

第二种方法也很简单，但危害性较大，建议不要在重要比赛中使用，否则可能让你追悔莫及。它就是：

#include<con>


//（windows系统中使用）

//或

#include</dev/console> 
//（Linux系统中使用）

它非常强大，可以卡住评测系统，使其永远停止不了编译你的程序。唯一的解除方法是，工作人员强行关机，重启，重测。当然，我不保证他们不会气愤地把你的成绩变成0分。请慎用此方法。

第8章实战演练

下面我们来做一些习题，练习骗分技巧。
我们来一起分析一下NOIP2013普及组的试题吧。

记数问题（NOIP普及组2013第一题）

(count.cpp/c/pas)

描述
试计算在区间 1 到 n 的所有整数中,数字 x(0 ≤ x ≤ 9)共出现了多少次?例如,在 1 到 11 中,即在 1、2、3、4、5、6、7、8、9、10、11 中,数字 1 出现了 4 次。

【输入】

输入文件名为 count.in。

输入共 1 行，包含 2 个整数 n、x，之间用一个空格隔开

【输出】

输出文件名为 count.out。

输出共 1 行，包含一个整数，表示 x 出现的次数。

【输入输出样例】

count.in count.out

11 1 4
限制
每个测试点1s。

【数据说明】

对于 100%的数据，1≤ n ≤ 1,000,000，0 ≤ x ≤ 9。

表达式求值（noip2013普及组第二题）

(expr.cpp/c/pas)

描述
给定一个只包含加法和乘法的算术表达式,请你编程计算表达式的值。

【输入】

输入文件为 expr.in。

输入仅有一行，为需要你计算的表达式，表达式中只包含数字、加法运算符“+”和乘 ，且没有括号，所有参与运算的数字均为 0 到 231-1 之间的整数。输入数据保 法运算符“\*”

证这一行只有 0~ 9、+、\*这 12 种字符。

【输出】

输出文件名为 expr.out。

输出只有一行，包含一个整数，表示这个表达式的值。注意：当答案长度多于 4 位时，

请只输出最后 4 位，前导 0 不输出。

【输入输出样例 1】

expr.in expr.out

1+1\*3+4 8

【输入输出样例 2】

expr.in expr.out

1+1234567890\*1 7891

【输入输出样例 3】

expr.in expr.out

1+1000000003\*1 4

【输入输出样例说明】

样例 1 计算的结果为 8，直接输出 8。

样例 2 计算的结果为 1234567891，输出后 4 位，即 7891。

样例 3 计算的结果为 1000000004，输出后 4 位，即 4。

【数据范围】

对于 30%的数据，0≤表达式中加法运算符和乘法运算符的总数≤100；

对于 80%的数据，0≤表达式中加法运算符和乘法运算符的总数≤1000；

对于 100%的数据，0≤表达式中加法运算符和乘法运算符的总数≤100000。

小朋友的数字（noip2013普及组第三题）(number.cpp/c/pas)

描述
有 n 个小朋友排成一列。每个小朋友手上都有一个数字,这个数字可正可负。规定每个小朋友的特征值等于排在他前面(包括他本人)的小朋友中连续若干个(最少有一个)小朋友手上的数字之和的最大值。 作为这些小朋友的老师,你需要给每个小朋友一个分数,分数是这样规定的:第一个小朋友的分数是他的特征值,其它小朋友的分数为排在他前面的所有小朋友中(不包括他本人),小朋友分数加上其特征值的最大值。

请计算所有小朋友分数的最大值,输出时保持最大值的符号,将其绝对值对 p 取模后输出。

格式
【输入】

输入文件为 number.in。

第一行包含两个正整数 n、p，之间用一个空格隔开。

第二行包含 n 个数，每两个整数之间用一个空格隔开，表示每个小朋友手上的数字。

【输出】

输出文件名为 number.out。

输出只有一行，包含一个整数，表示最大分数对 p 取模的结果。

【输入输出样例 1】

number.in number.out

5 997 21

1 2 3 4 5

【输入输出样例说明】

小朋友的特征值分别为 1、3、6、10、15，分数分别为 1、2、5、11、21，最大值 21

对 997 的模是 21。

【输入输出样例 2】

第2/4页

number.in number.out

5 7 -1
-1 -1 -1 -1 -1

【输入输出样例说明】

小朋友的特征值分别为-1、-1、-1、-1、-1，分数分别为-1、-2、-2、-2、-2，最大值 -1 对 7 的模为-1，输出-1。

【数据范围】

对于 50%的数据，1 ≤ n ≤ 1,000，1 ≤ p ≤ 1,000所有数字的绝对值不超过 1000；

99 对于 100%的数据，1 ≤ n ≤ 1,000,000， 1≤ p ≤ 10， 其他数字的绝对值均不超过 10。

车站分级（NOIP普及组2013第四题）(level.cpp/c/pas)

描述
一条单向的铁路线上,依次有编号为 1, 2, ..., n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。

(注意:起始站和终点站自然也算作事先已知需要停靠的站点)

例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。

现有 m 趟车次的运行情况（全部满足要求） ，试推算这 n 个火车站至少分为几个不同的 级别。

【输入】

输入文件为 level.in。

第一行包含 2 个正整数 n, m，用一个空格隔开。

第 i + 1 行（1 ≤ i ≤ m）中，首先是一个正整数 si（2 ≤ si ≤ n），表示第 i 趟车次有 si 个停

靠站；接下来有 si 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个 空格隔开。输入保证所有的车次都满足要求。

【输出】

输出文件为 level.out。

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

第3/4页

【输入输出样例】

【数据范围】

对于 20%的数据，1 ≤ n, m ≤ 10； 对于 50%的数据，1 ≤ n, m ≤ 100； 对于 100%的数据，1 ≤ n, m ≤ 1000。

第4/4页
第1题，太弱了，不用骗，得100分。
第2题，数据很大，但是可以直接输入一个数，输出它mod 10000的值。得10分。
第3题，是一道非常基础的DP，但对于不知DP为何物的蒟蒻来说，就使用暴力算法（即DFS）。得20分。
第4题，我们可以寻找一下数据的规律，你会发现，在所有样例中，M值即为答案。所以直接输出M，得10分。
这样下来，一共得140分，比一等分数线还高20分！你的信心一定会得到鼓舞的。这就是骗分的神奇。

第9章结语

骗分是蒟蒻的有力武器，可以在比赛中骗得大量分数。相信大家在这本书中收获了很多，希望本书能帮助你多得一些分。
但是，最后我还是要说一句：
$\color{Lime}\texttt{“ 不骗分，是骗分的最高境界。”}$

最长子序列(排序)

尺取法:

用途:

O(n)时间
求数组内和大于/小于 S的最短/长子序列长度为几。

方法:

i前j后，i每次++，并将a[i]加进和中，

求最短:

则j能加则加。

求最长:

则j要加则加。

特殊(特定)要求数列:

把 $ a_{1} a_{2} … a_{n} $(无序）

变成 $ b_{1} b_{2} … b_{n} $(特殊顺序）

方法:

初始化:

设 $ b_{1} b_{2} … b_{n} $

为 1 2 … n (d数组)

从头遍历b数组
再每次从头遍历a数组

如果 $b_{i} == a_{j}$ 且 $a_{i}$ 未设新值(c数组)

则 $a_{i}$ (c数组) 设为 $b_{i}$ 的设值(d数组)

排序:

使用正常排序方法排序d数组(连带a数组)

若求最少次数(交换次数)则用稳定排序

若让输出排序后序列
则可以直接输出b数组(保证正确情况下)(偷笑)

二进制

去掉数字$ (a)_2 $ 的最后面的一个 $1)_2$ :

a=a&(~x+1);
或
a=a&(-a);

a=a&(a-1)

线段树

构成:
图形构成:
		    1~8
        /        \
      1~4        5~8
     /   \      /   \
   1~2   3~4   5~6  7~8
   / \   / \   / \  / \
  1  2  3  4  5  6  7  8
数值构成：

层1:1~n

层2:1~n/2 n/2+1~n

层3:1~n/4 n/4+1~n/2 n/2+1~n/4*3 n/4*3+1~n

层4:1~n/8 n/8+1~n/4 n/4+1~n/8*3 n/8*3+1~n/2 n/2+1~n/8*5 n/8*5+1~n/4*3 n/4*3+1~n/8*7 n/8*7+1~n

…

逻辑构成:

将整个数组尽量等分成两份，把每份当做整个数组重复进行，直到每份都代表一个变量则结束。

圆形拆分

当题目中有圆形时，可以将圆形按份数m(通用或题目说明)展开成矩形，面积与周长公式进行等价变化，并将a[1]与a[m]连接。

差分

适用范围:

当在一个一维数组上，将某一条连续的变量增加或减少时使用

使用方法:

当要将a[s]~a[t]增加r时，可以在a[s]上加r,a[t+1]上加-r。

输出(或求值):

输出整个数组中的值时，可以设一个h，从a[0]开始遍历，每次加上a[i]的值，然后输出h。

并查集

适用范围:

当在图中(有向无环图)可以使用。

使用方法:

主体:

将图按照拓补排序规则进行构造，形成森林。

构造:

设每一条边用(u,v,w)表示，随后对每条边以w的值从小到大排序，最后用贪心的方法进行构造(每次选当前最短的边，判断u和v是否联通，若不联通则将当前边加入，最后将边删除)

联通比较:

不断让两个节点寻找根节点，若根节点一致则相互联通。

集合合并:

将较小的集合(树)的根节点连到较大的集合(树)的根节点上。

最早公共祖先:

开一个二维数组f,f[i][j]代表第i个点的第 $2^{j}$ 的祖先，f[i][j]=f[f[i][j-1]][j-1]

路径压缩:

在寻找根节点时，将路径上所有节点的父节点改为根节点，(提高之后比较效率)（不可回溯）。

前缀和

定义:

将从(0,0),到(n,m)的总和存在点(n,m)里,以方便计算某个部分的和。

方法:

一维:

qz[0]=a[0],qz[i]=qz[i-1]。

二维:

qz[0][0]=a[0][0],qz[i][j]=qz[i-1][j]+qz[i][j-1]-qz[i-1][j-1]+a[i][j]。

哈希

中心:

把较大/多的数据用较小/少的内存存下来(满足某种要求)(多半用于桶排序)。

方式:

把较大的数据用固定的方式存下来。

思路:

开放寻址，新空间不定存几(投机)。

其它:

哈希表

素数与半素数

素数:

半素数(两个素数相乘):

求出n以内的半素数个数:

设一共h个，先求出i(2~n)以内的素数个数，并存到a[i]里面，同时将素数存到b数组里，再遍历b数组，判断n/b[i]>=b[i]否。

若为真，则 h=h+a[n/b[i]]-a[b[i]]+1；

若为假，则返回h，并结束程序。