SDUTOJ2498---AOE网上的关键路径

最新推荐文章于 2022-07-21 19:45:26 发布

原创

最新推荐文章于 2022-07-21 19:45:26 发布 · 438 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #算法 #分治算法 #图论 #dijkstra

博客围绕有向无环图（DAG）的关键路径求解展开。介绍了AOE网概念，给出输入输出要求及样例。指出求最长路径可将权值加负号或改变松弛条件，但Dijkstra算法不适用。推荐用SPFA算法减少复杂度，还提到反向建图方便输出路径，也可使用Bellman - Ford实现。

题目描述

一个无环的有向图称为无环图（Directed Acyclic Graph），简称DAG图。
AOE(Activity On Edge)网：顾名思义，用边表示活动的网，当然它也是DAG。与AOV不同，活动都表示在了边上，如下图所示：

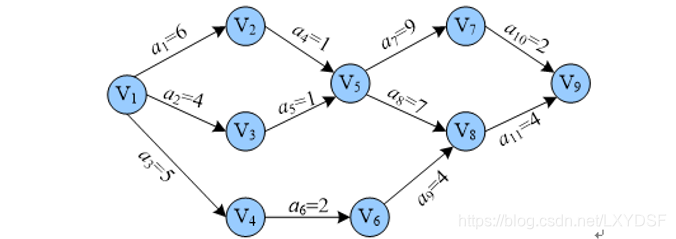
在这里插入图片描述

如上所示，共有11项活动（11条边），9个事件（9个顶点）。整个工程只有一个开始点和一个完成点。即只有一个入度为零的点（源点）和只有一个出度为零的点（汇点）。
关键路径：是从开始点到完成点的最长路径的长度。路径的长度是边上活动耗费的时间。如上图所示，1 到2 到 5到7到9是关键路径（关键路径不止一条，请输出字典序最小的），权值的和为18。

Input

这里有多组数据，保证不超过10组，保证只有一个源点和汇点。输入一个顶点数n(2<=n<=10000),边数m(1<=m <=50000),接下来m行，输入起点sv，终点ev,权值w（1<=sv,ev<=n,sv != ev,1<=w <=20)。数据保证图连通。

Output

关键路径的权值和，并且从源点输出关键路径上的路径（如果有多条，请输出字典序最小的）。

输入样例

输出样例

思路:
这个题的意思是让求源点和汇点的关键路径并输出,当有多条时,输出字典序最小的那个.
求最长路径,可以将权值加负号来求解,也可以改变松弛条件,距离大的更新.而Dijkstra算法无法处理负权边,也没有办法通过改变松弛条件来求解最长路(因为它用到了贪心的思想).求解最长路有一下两种方法:

按照拓扑序列求解最长路.
按照Bellman或SPFA算法,改变松弛条件,求解最长路.

但由于Bellman算法时间复杂度是O( n * m),可能会超时,所以为了减少复杂度需要使用SPFA算法,该复杂度是O(k * m),k是一个很小的数,最多为O(n*m)

其次由于要输出路径,而且路径要按照字典序选取,所以反向建图会更方便的输出(如果正向建图则需要借助于栈来进行输出,如果数据量大,可能通不过)

我们在进行前驱节点进行编号时,如果该节点的邻接点+中间的边后dis更长,则更新dis和前驱p.如果路径相等,但该节点的号更小则仍只更新前驱p.

这个题也可以使用Bellman-Ford实现.还可以一边求拓扑一边进行松弛,后序进行补充!

参考代码

#include<iostream>
#include<string.h>
#include<queue>
#include<stack>
using namespace std;
const int maxv = 10000+10,maxe = 50000+10,INF = 0xc0c0c0c0;
int head[maxv],dis[maxv],p[maxv],in[maxv],out[maxv],vis[maxv],num,n,m;
struct Edge{
   
   
	int next,to,w;
}e[maxe];

void add(int u,int v,int w){
   
   
	e[++num].to = v;
	e[num].w = w;
	e[num].next = head[u];
	head[u] = num;	
}

void SPFA(int u){
   
   
	for(int i = 1; i <= n; i++){
   
   
		dis[i]  =INF;
	}
	queue<int> q;
	q.push(u);
	vis[u<