DDPM（扩散模型）：以自己能够理解的角度梳理一下

Denoising Diffusion Probabilistic Models

去噪扩散概率模型。总得来说分为两个过程；

• 前向过程（加噪）

  • 一个不断加标准高斯噪声（破坏图像）的一个过程。
  • 当时间 $t$ 足够大时，我们可以认为此时的图像近似为一张纯高斯噪声图像 ${\mathbf{x}}_T$。

• 反向过程（去噪）

  • 采样一个标准的高斯噪声 ${\mathbf{x}}_T$，让网络对其逐步去噪 ${\mathbf{x}}_{T-1},{\mathbf{x}}_{T-2},\dots$ ，最终得到没有噪声的图像 ${\mathbf{x}}_0$ 。

用粗略的话讲，模型学习在每个时间 $t$ 加多少噪声，去多少噪声，那么自然就可以从一张标准的高斯噪声恢复出真实图像。

---

前向过程

前向过程也称为扩散过程，将真实数据逐步变成噪声。

从单个图像（ 原始图像表示为： ${\mathbf{x}}_0$）来看，我们添加一次 「标准」高斯噪声 $\mathbf{ϵ}\sim \mathcal{N}(0,\mathbf{I})$，得到 ${\mathbf{x}}_1$。记 ${\mathbf{x}}_i$ 为对原始图像加 $i$ 次噪声后的结果。 当时间 $i$ 足够大的时候，数据会被高斯噪声淹没，变成纯正的高斯噪声。

上图的扩散过程从 ${\mathbf{x}}_0$ 一直到 ${\mathbf{x}}_T$ 就是一个马尔可夫链，表示状态空间中经过从一个状态到另一个状态的转换的随机过程。

• 至于什么是马尔可夫链，后续打算单独讲（简单来讲就是当前状态只于前一个状态有关）

首先第一个问题，加多少次噪声？

在文中，其由一个超参数$T$控制，即步数。原文$T=1000$, 即对原始图像加1000次噪声后，其会变成完全的高斯噪声。

那么噪声怎么加呢?

加噪声的过程其实是一个加权的过程。比如 $0.8\times Image+0.1\times Noise$，我们需要弄清楚的就是权重系数的问题，噪声的权重我们可以称之为扩散率。

直觉上来说，加噪对图像原有的信息应该是是慢慢破坏的(扩散率很低)，也就是说扩散率应该是在慢慢增大。这样主要是为了方便网络在逆扩散过程中学习去噪。

也就是说——去噪的过程是先把"明显"的噪声给去除，对应着较大的扩散率；当去到一定程度，逐渐逼近真实真实图像的时候，去噪速率逐渐减慢，开始微调，也就是对应着较小的扩散率。

> 重要公式 1 <

$${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{ϵ}}_t,{\mathbf{ϵ}}_t\sim \mathcal{N}(0,\mathbf{I})$$

原文中还有一个符号是 ${\beta }_t$ , 两者关系是 ${\alpha }_t=1-{\beta }_t$，所以也有：

$${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{\mathbf{ϵ}}_t,{\mathbf{ϵ}}_t\sim \mathcal{N}(0,\mathbf{I})$$

上述公式其实就是提到的 $a\times Image+b\times Noise$。其中 $Image$ 是 ${\mathrm{x}}_{t-1}$，$Noise$ 是 ${ϵ}_t$ 。前向过程噪声是在逐步增加，对应着 $\sqrt{1-{\alpha }_t}$ 在逐步减小。

前向过程：${\beta }_t$ 在逐步减小，${\alpha }_t$ 在逐步增大；

对于大多数文章来说，经常出现下面这个式子

$$q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$$

需要说明的是 ${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}{\mathbf{ϵ}}_{t-1}$ 和 $q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})=\mathcal{N}({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I})$ 是等价的，参考前置知识中的 「重参数化技巧」 ，$ϵ=\mu +\mathbf{z}\cdot \sigma$ 表述的就是从 $ϵ\sim \mathcal{N}(\mu ,{\sigma }^2)$ 中采样的过程。

任意时刻的 ${\mathbf{x}}_t$ 由 ${\mathbf{x}}_0$ 表示

这里存在一个低效的问题。在马尔可夫链中，当我们需要潜在样本 ${\mathbf{x}}_t$ 时，我们必须在马尔可夫链中执行 $t-1$ 步。

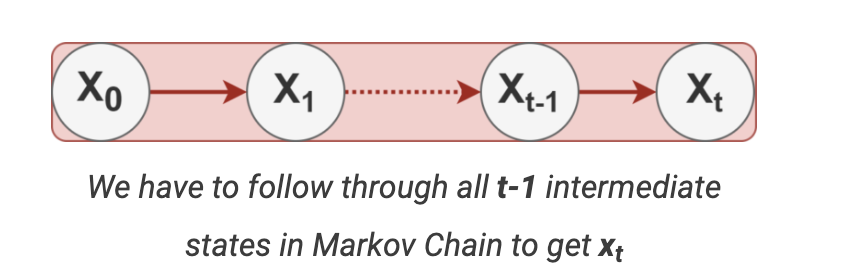
为了解决这个问题，作者优化了步骤，直接从 timesteps = 0(即 ${\mathbf{x}}_0$) 推导到扩散过程中的${\mathbf{x}}_t$。

接下来，我们可以了解如何用数学来解释这个扩散过程。给定当前具有一定噪声的图像${\mathrm{x}}_{t-1}$, 加入标准高斯噪声噪声${ϵ}_{t-1}\sim$ $\mathcal{N}(0,\mathbf{I})$, 得到进一步加噪的图像${\mathbf{x}}_t$, 我们可以建模成：

$${\mathrm{x}}_t=a_t{\mathrm{x}}_{t-1}+b_t{ϵ}_t,{\mathbf{ϵ}}_t\sim \mathcal{N}(0,\mathbf{I})\text{\hspace{1em}(1)}$$

因为 ${\mathrm{x}}_{t-1}$ 具有的信息更多，因此 $a_t$ 是一个衰减系数，值应该满足 $0<a_t<1$ ; 同样的噪声系数也满足 $0<b_t<1$ 。

当我们用 ${\mathbf{x}}_{t-1}=a_{t-1}{\mathbf{x}}_{t-2}+b_{t-1}{\mathbf{ϵ}}_{t-1}$ 不断展开这个式子, 可以得到：

$$\begin{array}{rl}{\mathbf{x}}_t& =a_t{\mathbf{x}}_{t-1}+b_t{\mathbf{ϵ}}_t\\ & =a_t(a_{t-1}{\mathbf{x}}_{t-2}+b_{t-1}{\mathbf{ϵ}}_{t-1})+b_t{\mathbf{ϵ}}_t\\ & =a_t{a}_{t-1}{\mathbf{x}}_{t-2}+a_t{b}_{t-1}{\mathbf{ϵ}}_{t-1}+b_t{\mathbf{ϵ}}_t\\ & =\dots \\ & =(a_t\dots a_1){\mathbf{x}}_0+(a_t\dots a_2)b_1{\mathbf{ϵ}}_1+(a_t\dots a_3)b_2{\mathbf{ϵ}}_2+\cdots +a_t{b}_{t-1}{\mathbf{ϵ}}_{t-1}+b_t{\mathbf{ϵ}}_t\end{array}\text{\hspace{1em}(2)}$$

除了第一项，后面是多个独立正态分布的的和。 前面有说 $ϵ$ 其实是标准高斯噪声，那么 ${ϵ}_i$ 本质上是同属于一个分布 $\mathcal{N}(0,\mathbf{I})$ 下的 不同采样。

利用叠加性，他们的和也是一个正态分布，均值为 0， 方差为 $(a_t\dots a_2{)}^2{b}_1^2+(a_t\dots a_3{)}^2{b}_2^2+\cdots +a_t^2{b}_{t-1}^2+b_t^2.$

这样原表达式可以写成

$$\begin{array}{c}{\mathbf{x}}_t=(a_t\dots a_1){\mathbf{x}}_0+\sqrt{(a_t\dots a_2{)}^2{b}_1^2+(a_t\dots a_3{)}^2{b}_2^2+\cdots +a_t^2{b}_{t-1}^2+b_t^2}{\overline{\mathbf{ϵ}}}_t,\\ {\overline{\mathbf{ϵ}}}_t\sim \mathcal{N}(0,\mathbf{I})\end{array}\text{\hspace{1em}(3)}$$

重参数化技巧

对高斯分布 $\mathcal{N}(\mu ,{\sigma }^2)$ 进行采样一个噪声，等价于先从标准高斯分布 $\mathcal{N}(0,1)$ 中采样的到一个噪声 $\mathbf{z}$, 乘上标准差 $\sigma$，再加上均值 $\mu$ , 即： $ϵ=\mu +\mathbf{z}\cdot \sigma$

这里有一个细节，如果我们把系数的平方和都加起来

$$\begin{array}{rl}& (a_t\dots a_1{)}^2+(a_t\dots a_2{)}^2{b}_1^2+(a_t\dots a_3{)}^2{b}_2^2+\cdots +a_t^2{b}_{t-1}^2+b_t^2\\ & =(a_t\dots a_2{)}^2{a}_1^2+(a_t\dots a_2{)}^2{b}_1^2+(a_t\dots a_3{)}^2{b}_2^2+\cdots +a_t^2{b}_{t-1}^2+b\\ & =(a_t\dots a_2{)}^2(a_1^2+b_1^2)+(a_t\dots a_3{)}^2{b}_2^2+\cdots +a_t^2{b}_{t-1}^2+b_t^2\\ & =(a_t\dots a_3{)}^2\left(a_2^2(a_1^2+b_1^2)+b_2^2\right)+\cdots +a_t^2{b}_{t-1}^2+b_t^2\\ & =a_t^2(a_{t-1}^2\left(\dots \left(a_2^2(a_1^2+b_1^2)+b_2^2\right)+\dots \right)+b_{t-1}^2)+b_t^2\end{array}\text{\hspace{1em}(4)}$$

我们发现，如果加一个约束 $a_t^2+b_t^2=1$ ,上面括号里的平方和就为 1 了。同时如果我们记 ${\bar{a}}_t=(a_t\dots a_1{)}^2$ ， 那么平方和的后面部分，即式 $(3)$的方差部分，就可以表示为 $1-{\bar{a}}_t$ 。 那么式 $(3)$ 就可以改写:

$${\mathbf{x}}_t=\sqrt{{\bar{a}}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{a}}_t}{\overline{\mathbf{ϵ}}}_t,{\overline{\mathbf{ϵ}}}_t\sim \mathcal{N}(0,\mathbf{I})\text{\hspace{1em}(5)}$$

• 我们把 $a$ 替换成 $\alpha$

$${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\overline{\mathbf{ϵ}}}_t,{\overline{\mathbf{ϵ}}}_t\sim \mathcal{N}(0,\mathbf{I})\text{\hspace{1em}(6)}$$

• 接着写出式 $(6)$ 对应的概率形式

$${\mathbf{x}}_t\sim q({\mathbf{x}}_t|{\mathbf{x}}_0)=\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,(1-{\bar{\alpha }}_t)\mathbf{I}),{\bar{\alpha }}_t=\prod _{i=1}^t{\alpha }_i\text{\hspace{1em}(7)}$$

到这里已经是和原论文一致了。这里花一定篇幅来讲解 $\alpha$ 和 $\beta$ 的系数设置；
同时还有对于均值 ${\sqrt{\alpha }}_t$ 的设置 ，很多博客的观点如下：

• $T\to \infty \text{,}{x}_T\sim \mathcal{N}(0,\mathbf{I})$ ，最后是一个标准正态分布，因此前一项的接近0，后项应该设计成一个$\sqrt{1-{\alpha }_t}$ 的形式。
• ${\sqrt{\alpha }}_t$ 的系数能够稳定保证最后收敛到方差为1的标准高斯分布；

我觉得对于我来说更多的是推导的简洁优雅。毕竟是先有假设 $a_t^2+b_t^2=1$ , 才会有最后的结果。

整个前向过程是一个后验估计，被表示为：（根据联合概率密度+马尔可夫链性质）

$$q({\mathbf{x}}_{1:T}|{\mathbf{x}}_0)=\prod _{t=1}^{T}q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\text{\hspace{1em}(8)}$$

---

反向过程

扩散过程是从原始数据 ${\mathbf{x}}_0$ 逐渐添加噪声得到 ${\mathbf{x}}_T$ 。 逆扩散过程就是从 ${\mathbf{x}}_T$ 逐步去噪得到 ${\mathbf{x}}_0$，即求：

$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$$

那么 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$ 怎么求呢？

首先加噪过程中 $q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})$ 我们是知道的，因此根据贝叶斯公式有

$$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)=\frac{q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1})}{q({\mathbf{x}}_t)}\text{\hspace{1em}(9)}$$

补充贝叶斯公式:
$$P(A|B)=\frac{P(B|A)\times P(A)}{P(B)}$$
多变量贝叶斯公式
$$P(A|B,C)=P(A,B,C)/P(B,C)$$
贝叶斯公式实现了概率反转，即由 $P(B|A)$ 得到 $P(A|B)$

现在问题是 $q({\mathbf{x}}_t)$ 和 $q({\mathbf{x}}_{t-1})$ 不知道。当 $T$ 足够大的时候，$q({\mathbf{x}}_T)$ 可以认为就是标准高斯噪声。但是我们并不知道具体的某个样本的值包含多少图像信息，因此我们我们是无法知道 $q({\mathbf{x}}_t)$ 的。

要想知道 $q({\mathbf{x}}_t)$ 和 $q({\mathbf{x}}_{t-1})$ ，自然就依赖于一个先决条件，没加噪声的图像 $q({\mathbf{x}}_0)$ 。换句话说，$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)$ 和 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)$ 我们是知道的。如果我们在 式$(9)$ 再加上一个条件 ${\mathbf{x}}_0$ , 将求解 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$ 转换成求解 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t,{\mathbf{x}}_0)$ 。这样可以得到多元条件分布

$$\begin{array}{rl}q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)& =\frac{q({\mathbf{x}}_{t-1},{\mathbf{x}}_t,{\mathbf{x}}_0)}{q({\mathbf{x}}_t,{\mathbf{x}}_0)}\\ & =\frac{q({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1},{\mathbf{x}}_0)q({\mathbf{x}}_t\mid {\mathbf{x}}_0)q({\mathbf{x}}_0)}{q({\mathbf{x}}_t\mid {\mathbf{x}}_0)}\end{array}\text{\hspace{1em}(10)}$$

• 由于扩散过程是一个马尔可夫过程，${\mathbf{x}}_t$ 只和前一个状态 ${\mathbf{x}}_{t-1}$ 有关，和 ${\mathbf{x}}_0$ 无关；
• 另外 ${\mathbf{x}}_0$ 是原始样本，是已知的；

那么继续求解 式$(10)$ 有

$$q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{q({\mathbf{x}}_t|{\mathbf{x}}_0)}\text{\hspace{1em}(11)}$$

那么如何求解 式 $(11)$ 呢？

现在我们存在一个问题，在反向去噪过程中，根据 式 $(11)$ ，我们发现从 ${\mathbf{x}}_t$ 推断 ${\mathbf{x}}_{t-1}$ 需要建立在 ${\mathbf{x}}_0$ 已知的情况。但去噪过程中，${\mathbf{x}}_0$ 本身就是我们需要去求解的东西。所以我们需要进一步拆解上述式子。「看看能不能把 ${\mathbf{x}}_0$ 消除掉」 。如果消除掉，就不用陷入这种求 ${\mathbf{x}}_0$ 必须知道 ${\mathbf{x}}_0$ 的困境了。

• $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 等价于 ${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}{\mathbf{ϵ}}_t$ 。 写成分布的形式，有 $\mathcal{N}({\mathbf{x}}_t;\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1},1-{\alpha }_t\mathbf{I})$ 。 进一步写成概率密度函数的形式，$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)\propto \exp (-\frac{1}{2}\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{1-{\alpha }_t})=\exp (-\frac{1}{2}\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{{\beta }_t})$ 。

• $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)$ 等价于 ${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_{t-1}}{\overline{ϵ}}_{t-1}$ 。 写成分布的形式，有 $\mathcal{N}({\mathbf{x}}_{t-1};\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0,1-{\bar{\alpha }}_t\mathbf{I})$ 。 进一步写成概率密度函数的形式，$q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0)\propto \exp (-\frac{1}{2}\frac{({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_{t-1}})。$

• $q({\mathbf{x}}_t|{\mathbf{x}}_0)$ 等价于 ${\mathbf{x}}_t=\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0+\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t$ 。 写成分布的形式，有 $\mathcal{N}({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,1-{\bar{\alpha }}_t\mathbf{I})$ 。 进一步写成概率密度函数的形式，$q({\mathbf{x}}_t\mid {\mathbf{x}}_0)\propto \exp (-\frac{1}{2}\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t})$ 。

这里为什么要把概率密度函数的形式给拿出来呢？其实是方便运算。

因此 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\times q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)÷q({\mathbf{x}}_t|{\mathbf{x}}_0)$，写成密度函数的形式为有

$$\begin{array}{rl}q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)& =q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})\frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{q({\mathbf{x}}_t|{\mathbf{x}}_0)}\\ & \propto \exp \left(-\frac{1}{2}(\frac{({\mathbf{x}}_t-\sqrt{{\alpha }_t}{\mathbf{x}}_{t-1}{)}^2}{{\beta }_t}+\frac{({\mathbf{x}}_{t-1}-\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_{t-1}}-\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t})\right)\\ & =\exp \left(-\frac{1}{2}(\frac{{\mathbf{x}}_t^2-2\sqrt{{\alpha }_t}{\mathbf{x}}_t{\mathbf{x}}_{t-1}+{\alpha }_t{\mathbf{x}}_{t-1}^2}{{\beta }_t}+\frac{{\mathbf{x}}_{t-1}^2-2\sqrt{{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0{\mathbf{x}}_{t-1}+{\bar{\alpha }}_{t-1}{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_{t-1}}-\frac{({\mathbf{x}}_t-\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{)}^2}{1-{\bar{\alpha }}_t})\right)\\ & =\exp \left(-\frac{1}{2}(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})x_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)x_{t-1}+C({\mathbf{x}}_t,{\mathbf{x}}_0)\right)\end{array}$$

tips: 技巧性化简，我们所有的转换、化简都是为了求关于 ${\mathbf{x}}_{t-1}$ 的条件分布 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_0,{\mathbf{x}}_0)$ 。基于此，所以我们把 ${\mathbf{x}}_{t-1}$ 给提取出来
$$C({\mathbf{x}}_t,{\mathbf{x}}_0)=\frac{{\mathbf{x}}_t^2-2\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0{\mathbf{x}}_t+{\bar{\alpha }}_t{\mathbf{x}}_0^2}{1-{\bar{\alpha }}_t}$$
$C({\mathbf{x}}_t,{\mathbf{x}}_0)$ 为不涉及 ${\mathbf{x}}_{t-1}$ 的项，所以忽略

那么上面这个整理的式子究竟有什么用呢？ 回顾下，以 $x$ 为自变量的高斯分布 $\mathcal{N}(\mathbf{x};\mu ,{\sigma }^2)$ , 其概率密度函数正比于 $\exp (-\frac{1}{2}(\frac{1}{{\sigma }^2}{x}^2-\frac{2\mu }{{\sigma }^2}x+\frac{{\mu }^2}{{\sigma }^2}))$ 。可以发现, 上面式子中 ${\mathbf{x}}_{t-1}^2$ 与 ${\mathbf{x}}_{t-1}$ 的系数，其中就包含了 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$ 的均值和方差的信息。

我们发现 方差 ${\sigma }^2$ 就是 $x^2$ 的系数的倒数。而 ${\mathbf{x}}_{t-1}^2$ 的系数为 $(\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}})$ ，完全只由人工确定的超参数 $\alpha$ 和 $\beta$ 确定。因此方差是确定的，但是均值与 ${\mathbf{x}}_{t-1}$ 的系数 $(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{x}_0)$ 有关。可以发现，除了已知量 $\alpha$ 、 $\beta$ 和 ${\mathbf{x}}_t$ ，依然包含着我们想要消除的项 ${\mathbf{x}}_0$ 。

我们先整理一下有(${\alpha }_t+{\beta }_t=1$ and ${\bar{\alpha }}_t={\prod }_{i=1}^T{\alpha }_i$)：

$$\frac{1}{{\sigma }^2}=\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\bar{\alpha }}_{t-1}}=\frac{{\alpha }_t-{\bar{\alpha }}_t+{\beta }_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}=\frac{1-{\bar{\alpha }}_t}{{\beta }_t(1-{\bar{\alpha }}_{t-1})}\text{\hspace{1em}(13)}$$

$$⟹{\sigma }^2=\frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\text{\hspace{1em}(13-1)}$$

$$\begin{array}{r}\frac{2\mu }{{\sigma }^2}=(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{2\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)\end{array}\text{\hspace{1em}(14)}$$

$$\begin{array}{rl}⟹\mu & =(\frac{\sqrt{{\alpha }_t}}{{\beta }_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}}{1-{\bar{\alpha }}_{t-1}}{\mathbf{x}}_0)\cdot \frac{1-{\bar{\alpha }}_{t-1}}{1-{\bar{\alpha }}_t}\cdot {\beta }_t\\ & =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}{\mathbf{x}}_0\end{array}\text{\hspace{1em}(14-1)}$$

现在 $\mu$ 是一个只关于 ${\mathbf{x}}_0$ 和 ${\mathbf{x}}_t$ 的式子。我们记做 ${\tilde{\mathbf{\mu }}}_t({\mathbf{x}}_t,{\mathbf{x}}_0)$ , 简化为 ${\tilde{\mathbf{\mu }}}_t$ ；

前面说了在反向扩散阶段，${\mathbf{x}}_0$ 是不知道的。但是根据 ${\mathbf{x}}_0=\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t)$ ，有

$$\begin{array}{rl}{\tilde{\mathbf{\mu }}}_t& =\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}{\mathbf{x}}_t+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}({\mathbf{x}}_t-\sqrt{1-{\bar{\alpha }}_t}{\mathbf{ϵ}}_t)\\ & =(\frac{\sqrt{{\alpha }_t}(1-{\bar{\alpha }}_{t-1})}{1-{\bar{\alpha }}_t}+\frac{\sqrt{{\bar{\alpha }}_{t-1}}{\beta }_t}{1-{\bar{\alpha }}_t}\frac{1}{\sqrt{{\bar{\alpha }}_t}}){\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}\cdot \sqrt{{\alpha }_t}}{\mathbf{ϵ}}_t\\ & =(\frac{{\alpha }_t-{\bar{\alpha }}_t}{\sqrt{{\alpha }_t}\cdot (1-{\bar{\alpha }}_t)}+\frac{1-{\alpha }_t}{(1-{\bar{\alpha }}_t)\cdot \sqrt{{\alpha }_t}}){\mathbf{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}\cdot \sqrt{{\alpha }_t}}{\mathbf{ϵ}}_t\\ & =\frac{1}{\sqrt{{\alpha }_t}}\left({\mathrm{x}}_t-\frac{1-{\alpha }_t}{\sqrt{1-{\bar{\alpha }}_t}}{\mathbf{ϵ}}_t\right)\end{array}$$

到这一步，我们已经把 ${\mathbf{x}}_0$ 给消掉了。只要知道了 ${\mathbf{ϵ}}_t$ , 我们就可以把 ${\tilde{\mathbf{\mu }}}_t$ 给算出来，进而得到 $q({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t)$，采样出 ${\mathbf{x}}_{t-1}$，完成去噪的过程。

还没写完，有空再补吧！！！

---

参考

简单基础入门理解Denoising Diffusion Probabilistic Model，DDPM扩散模型
What are Diffusion Models?
由浅入深了解Diffusion Model

​