最近在为蓝桥杯(C++大学A组)做准备,打算拿蓝桥杯题库中的题目训练一下,有一段时间没有使用过C++编程了,毕竟学校的课程还是很紧张的,新内容很多,课外时间我也喜欢去尝试接触新的语言新的东西,于是想借此机会锻炼一下自己的C++编程能力(毕竟我是打算向着C/C++、C#方向发展)。在这个过程中发现了许多问题以及自己不了解的知识点,决定在优快云上记录一下,另外本人也大三了,整理一个自己的blog/github对将来考研或者找工作也有帮助嘛。
《审美课》这个问题不算是我遇到的第一个问题了吧,但是暂时还是从这个问题记录起。
问题描述
《审美的历程》课上有n位学生,帅老师展示了m幅画,其中有些是梵高的作品,另外的都出自五岁小朋友之手。老师请同学们分辨哪些画的作者是梵高,但是老师自己并没有答案,因为这些画看上去都像是小朋友画的……老师只想知道,有多少对同学给出的答案完全相反,这样他就可以用这个数据去揭穿披着皇帝新衣的抽象艺术了(支持帅老师 ^ _ ^)。
答案完全相反是指对每一幅画的判断都相反。
输入格式
第一行两个数n和m,表示学生数和图画数;
接下来是一个n*m的01矩阵A:
如果aij=0,表示学生i觉得第j幅画是小朋友画的;
如果aij=1,表示学生i觉得第j幅画是梵高画的。
样例输入
3 2
1 0
0 1
1 0
样例输出
2
样例说明
同学1和同学2的答案完全相反;
同学2和同学3的答案完全相反;
所以答案是2。
数据规模和约定
对于50%的数据:n<=1000;
对于80%的数据:n<=10000;
对于100%的数据:n<=50000,m<=20。
看到这个问题,加上它的关键字显示只有一个词——“逻辑”,我心里就想着:这题稳了,这还不简单吗?没有多加思考,第一反应就是“蛮力法”解决它,别问,问就是暴力解题!
1)输入矩阵的规格n,m,用一个二维数组a[n][m]表示;
2)再用一个双重循环输入矩阵的内容,完成对矩阵的初始化;
3)再用一个三重循环完成比对:
a)一重循环:i从0 ~ n - 1,表示要进行比对的a[i]序列;
b)二重循环:j从i + 1 ~ n,表示要与a[i]序列进行比对的a[j]序列;
c)三重循环:k从0 ~ m,依次对比a[i][k]与a[j][k]是否相同,若相同则立即break,当二重循环结束
以后,判断k与m是否相等,若相等,则说明两个序列完全相反,反之则不然。
多简洁清晰的思路呀,我自己都服了我自己在如此短的时间内就理清了整个过程,于是一阵噼里啪啦的敲击键盘过后,我的第一版代码“油然屏幕上”。
第一版代码
#include <iostream>
using namespace std;
int a[50000][20];
int main(int argc, char *argv[]) {
int n, m, ans = 0;
cin >> n >> m;//输入数组规模
if(n > 50000 || m > 20){
cout << "error";
return 0;
}
//通过输入为数组赋值
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> a[i][j];
}
}
//逐一比对
int i, j, k;
for(i = 0; i < n - 1; i++){
for(j = i + 1; j < n; j++){
for (k = 0; k < m; k++){
//若两个序列的某一位相同,则这两个序列必不可能完全相反,跳出循环,进行下一个比对。
if(a[i][k] == a[j][k]){
break;
}
}
if(k == m){
ans++;
}
}
}
cout << ans;
return 0;
}
本以为这样就100分满分了,谁知提交代码之后……
……
……
……
……
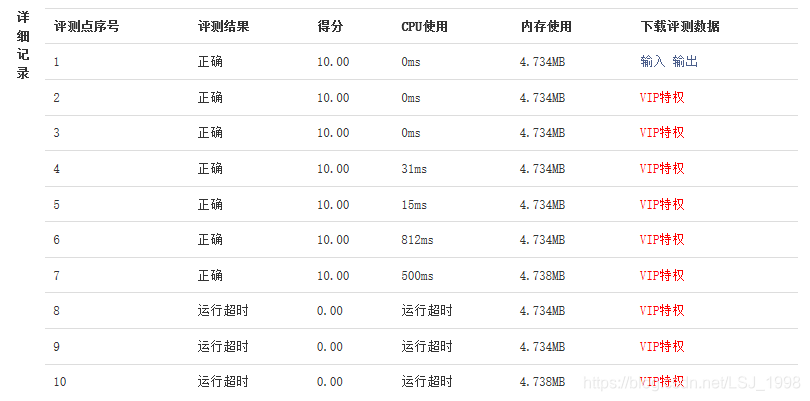
WTF?!运行超时!不要慌不要慌,一定是数组规模太大或者比较次数太多,导致数据量过大的时候运算复杂运算量比较大,这是在提醒我蛮力法解决不了这个问题,需要采用优化算法。在第二版代码出来以前,我脑海中闪过这么几种想法:
Plan A:不一行一行进行比对,而是竖着一列一列进行比对,比如说拿a[0]这个序列去进行比对的话,
首先将a[0][0]与a[1][0] ~ a[n][0]进行比对,找出与a[0][0]相反的所有序列,再在这些序列中进
行与a[0][1]的比对,以此类推……但是这个想法很快被我pass了,一是因为我觉得更加复杂,
特别是每次比对之后找出的相反的序列该怎么存储,二是因为我觉得这个想法和我采用的“蛮
力法”没有太大的区别,在时间复杂度上,最坏情况都是遍历完整个数组,在某种意义上和“蛮
力法”没有太大差别,反而搞的更复杂。
Plan B:当我在找与a[0]这个序列完全相反的序列时,我是要遍历剩余的所有序列的,那我能否记录下
与a[0]完全相同的序列,并且记录下它们的行号,当我在进行这些行的对比时,因为我对a[0]
进行过比对,且它们和a[0]完全相同,那么我可以省去这些行的遍历了。虽然这个想法可能
比“蛮力法”省去了很多比对的次数,但是我并没有去尝试,我始终没有找到一个很简洁的能够
存储这些相同序列的方法。
Plan C:这个想法就更是一闪而过就被我pass了。我想着对每一个序列进行比对时都构建一个二维数
组,第0行就是第一个序列,第0列就是第二个序列,a[i][i]表示两个序列的第i位是否相同,以
此来判断两个数组是否完全相反。没作多想,就觉得这样需要的内存会大得多,比对次数也
可能更多,pass。
实在没有办法了,在与室友进行讨论之后萌发了一个新的想法,就是用一个数组来存储每一个序列0或者1的个数,如果两个序列完全相反的话,那么这两个序列的0的个数之和一定为n(假设序列长度为n),那么就可以通过这个新的数组,来在比对前就判断即将进行比对的两个序列有没有比对的必要,这样就可以省去很多无效的比较,于是第二版代码应时而生。
第二版代码
#include <iostream>
using namespace std;
int a[50000][21]; //第21位用来存储该序列0的个数
int main(int argc, char *argv[]) {
int n, m, ans = 0;
cin >> n >> m;//输入数组规模
if(n > 50000 || m > 20){
cout << "error";
return 0;
}
//通过输入为数组赋值
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> a[i][j];
}
a[i][m] = 0;//序列a[i]中0的个数初始化为0
}
//计算每个序列中0的个数
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
if(a[i][j] == 0){
a[i][m]++;
}
}
}
int i, j, k;
for(i = 0; i < n - 1; i++){
for(j = i + 1; j < n; j++){
if(a[i][m] == a[j][m]){
for (k = 0; k < m; k++){
if(a[i][k] == a[j][k]){
break;
}
}
if(k == m){
ans++;
}
}
}
}
cout << ans;
return 0;
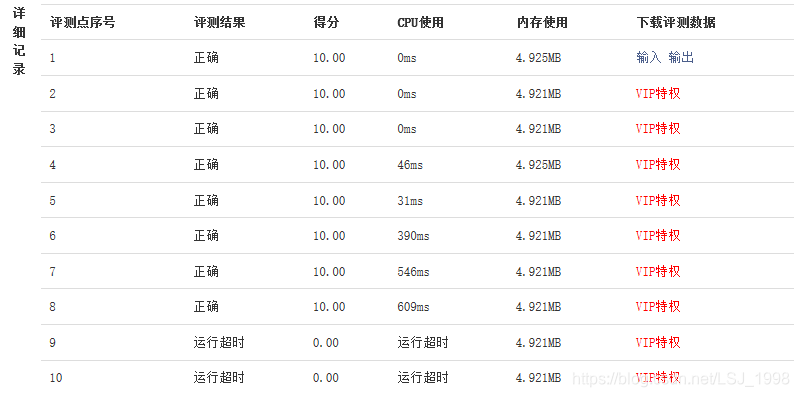
}好吧……得分比“蛮力法”稍微高了那么一点,在某些用例上也确实有优化,可是当数据过大的时候还是超时……万般无奈之下只得去借鉴大佬的做法。
第三版代码(搬运自优快云大佬)
#include<iostream>
using namespace std;
int m,n,A[50005];
int ans[2000000]={0};
int sum = 0;
int main(){
cin>>n>>m;//输入学生数和画数
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
int temp;
cin>>temp;
A[i] =(A[i]<<1)+temp;//2进制保存
}
ans[A[i]]++;//获得每个答案的人数
}
int max = (1<<m)-1;
for(int i=0;i<n;i++){
int temp = A[i]^max;//按位取反
sum += ans[temp] ;
}
cout<<sum/2<<endl;
return 0;
} 仔细研究了一下大佬的算法,实现了“精确匹配”,这样不需要在对每个序列比对时都遍历剩余的序列,粗略分析了一下,该算法的时间复杂度为O(n),而蛮力法的时间复杂度为O(n2)(如有不对望指正),事实上也确实如此,在数据量变大时也节省了巨额时间。
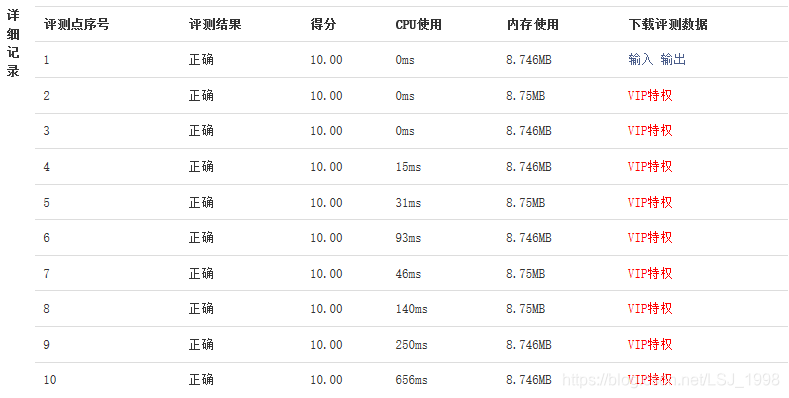
总结
总结一下从大佬的代码中学到的东西吧!首先是大佬的方法从某种意义上解决了我Plan B中的问题,如何来存储完全相同的两个序列:用一个长度为2m的一维数组,来表示对应每个十进制的值的二进制序列有多少个(或者说是“计数数组”),将相同的序列化为一“组”,能很大程度的减少无效比对,这也是我Plan B的思想。其次就是,用异或运算实现比对的效果,而且与哪个数进行异或也很巧妙,若二进制序列长度为n,则与1…1(n个1)进行异或(这里我觉得用非运算也可以,进而引发了我对异或运算与非运算的思考,详见(https://bbs.youkuaiyun.com/topics/392552616))如果说两两比对是漫无目的“扫荡”,那么异或运算就是实现了“精准打击”!对一个二进制序列对应的十进制i进行异或运算,得到了十进制数j,只需去查找a[j]对应的值,即可找到与该二进制序列完全相反的序列个数,可以说是更快更准,更加减少了无效运算的次数。最后就是输出结果上,一定要除以2,因为在这个算法中a与b完全相反计算了一次,b与a完全相反也计算了一次,进行了重复计数因此要除以2。
P.S.第一次发博,这个优快云的MarkDown编辑器可坑死我了……不知道是不是我用edge浏览器的原因,每次粘贴代码进来,这个编辑器就变为一片空白,也不能进行任何操作,有时候连把打好的内容选中都不行,只有重新再打一遍。搞得我后来每次插入代码之前都得先备份一下,提心吊胆的……




















 62
62

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








