数据结构 || 二叉树习题详解1

最新推荐文章于 2025-03-17 09:55:01 发布

布鲁克要补钙

最新推荐文章于 2025-03-17 09:55:01 发布

阅读量650

点赞数 1

分类专栏：笔记数据结构刷题文章标签：数据结构算法 c++

本文链接：https://blog.youkuaiyun.com/LQEmptycity/article/details/126702513

版权

笔记同时被 3 个专栏收录

54 篇文章

订阅专栏

数据结构

8 篇文章

订阅专栏

刷题

4 篇文章

订阅专栏

这篇博客详细解析了二叉树的各种遍历方法，包括前序、中序、后序遍历，并讨论了如何根据遍历序列唯一确定二叉树。此外，还介绍了层序遍历的应用，如计算二叉树的右视图、层平均值、最大深度和最小深度等，以及在填充节点的next指针和翻转二叉树等方面的问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

推导遍历结果

例题： 前序遍历序列为ABCDEF，中序遍历序列CBAEDF，请问后续遍历序列是？

先分析出A是根结点，那么从中序可以看出 B,C是A的左子树上结点，D,E,F是A的右子树上结点，在看B,C前序先输出B，则B是A的左孩子，C是B的结点，从中序可以看出先输出C,在输出B，则C是B的左孩子，同理前序可以看出D是A的右孩子，E,F是D的孩子结点，中序可以看出先输出E,D,F，则E是D的左孩子，F是D的右孩子。
最终二叉树为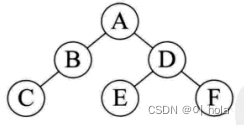
在这里插入图片描述

已知前序遍历序列和中序遍历序列，可以唯一确定一颗二叉树
已知后序遍历序列和中序遍历序列，可以唯一确定一颗二叉树
已知前序和后序遍历，不能唯一确定一颗二叉树

层序遍历相关

//二叉树的节点定义
struct TreeNode {
	int val;
	TreeNode* left;
	TreeNode* right;
	TreeNode(int x) :val(x), left(NULL), right(NULL) {	}
};

二叉树层序遍历

描述： 需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑

    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }

二叉树层次遍历2

层次遍历2

给定一个二叉树，返回其节点值自底向上的层次遍历（从叶节点所在层到根节点所在层，逐层从左向右遍历）

在这里插入图片描述

//给定一个二叉树，返回其节点值自底向上的层次遍历。
//（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历
//二叉树的层序遍历，就是最后把result数组反转一下就可以
vector<vector<int>> LevelOrder_2(TreeNode* root)//输出一个二维数组
{
	queue<TreeNode*> qu;
	vector<vector<int>> res;
	if (root != NULL) qu.push(root);
	while (!qu.empty())
	{
		int size = qu.size();
		// 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
		vector<int> vec;
		for (int i = 0; i < size; i++)
		{
			TreeNode* t = qu.front();
			qu.pop();
			vec.push_back(t->val);//把本层的节点数据都存入数组中
			if (root->left) qu.push(root->left); //把下一层的左右节点都入队列
			if (root->right) qu.push(root->right);
		}
		res.push_back(vec);
	}
	reverse(res.begin(), res.end());  //从底向上逐层输出
	return res;
}

二叉树的右视图

描述： 给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。
- 思路： 层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以

vector<int> rightSideView(TreeNode* root) {
	queue<TreeNode*> que;
	if (root != NULL) que.push(root);
	vector<int> result;   //一维数组存放返回节点数值
	while (!que.empty()) {
		int size = que.size();
		//size要先获取 不能使用que.size在for循环中 que.size()是不断变化的
		for (int i = 0; i < size; i++) {
			TreeNode* node = que.front();
			que.pop();
			if (i == (size - 1)) result.push_back(node->val); // 将每一层的最后元素放入result数组中
			if (node->left) que.push(node->left);
			if (node->right) que.push(node->right);
		}
	}
	return result;
}

二叉树的层平均值

描述： 给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。
思路： 层序遍历时把每一层求和再取一个平均值

vector<double> averagrofLevels(TreeNode* root) {
	queue<TreeNode*> que;
	if (root != NULL) que.push(root);
	vector<double> result;   //一维数组存放返回节点数值
	while (!que.empty()) {
		int size = que.size();
		//size要先获取 不能使用que.size在for循环中 que.size()是不断变化的
		double sum = 0;
		for (int i = 0; i < size; i++) {
			TreeNode* node = que.front();
			que.pop();
			sum += node->val;
			//sum用来求每一层节点数据值的总和
			if (node->left) que.push(node->left);
			if (node->right) que.push(node->right);
		}
		result.push_back(sum / size);
		//每一层的平均值放入结果集中
	}
	return result;
}

N叉树的层序遍历

描述： 给定一个 N 叉树，返回其节点值的层序遍历。(即从左到右，逐层遍历)
思路:
模板题，只不过一个节点有多个孩子
二叉树的层序遍历后存放左右孩子，N叉树层序遍历循环存放所有孩子结点

 vector<vector<int>> levelOrder(Node* root) {
        queue<Node*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            for (int i = 0; i < size; i++) { 
                Node* node = que.front();
                que.pop();
                vec.push_back(node->val);
                for (int i = 0; i < node->children.size(); i++) { // 将节点孩子加入队列
                    if (node->children[i]) que.push(node->children[i]);
                }
            }
            result.push_back(vec);
        }
        return result;

    }

在每个树行中找最大值

描述： 在二叉树的每一行中找到最大的值。
思路： 层序遍历取每一层最大值

vector<int> FindMax(TreeNode* root)
{
	queue<TreeNode*> que;
	vector<int> res;
	if (root != NULL) que.push(root);
	while (!que.empty())
	{
		int size = que.size();

		int max = 0;  //存放每一层的最大值
		for (int i = 0; i < size; i++)
		{
			TreeNode* node = que.front();
			que.pop();
			//if (node->val > max) max = node->val;
			max = node->val > max ? node->val : max;
			if (node->left) que.push(node->left);
			if (node->right) que.push(node->right);
		}
		res.push_back(max);
	}
	return res;
}

填充每一个节点的下一个右侧节点指针

描述： 给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。
思路： 层序遍历，只不过在单层遍历的时候记录一下本层的头部节点，然后在遍历的时候让前一个节点指向本节点就可以

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

struct Node {
	int val;
	Node* left;
	Node* right;
	Node* next;
};
Node* connect(Node* root) {
	queue<Node*> que;
	if (root != NULL) que.push(root);
	while (!que.empty()) {
		int size = que.size();
		vector<int> vec;
		Node* nodePre;
		Node* node;
		for (int i = 0; i < size; i++) {
			if (i == 0) {
				nodePre = que.front(); // 取出一层的头结点
				que.pop();
				node = nodePre;
			}
			else {
				node = que.front();
				que.pop();
				nodePre->next = node; // 本层前一个节点next指向本节点
				nodePre = nodePre->next;
			}
			if (node->left) que.push(node->left);
			if (node->right) que.push(node->right);
		}
		nodePre->next = NULL; // 本层最后一个节点指向NULL
	}
	return root;

}

二叉树的最大深度(层序遍历)

描述： 给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
思路： 使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，

int GetDepth(TreeNode* root)
{
	if (root == NULL) return 0;
	int depth = 0;
	queue<TreeNode*> que;
	que.push(root);
	while (!que.empty()) {
		int size = que.size();
		depth++; // 记录深度
		for (int i = 0; i < size; i++) {
			TreeNode* node = que.front();
			que.pop();
			if (node->left) que.push(node->left);
			if (node->right) que.push(node->right);
		}
	}
	return depth;
}

二叉树的最小深度

描述： 只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点
思路： 在二叉树中，一层一层的来遍历二叉树，找到左右孩子都为空时，则找到最小深度

    int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        int depth = 0;
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()) {
            int size = que.size();
            depth++; // 记录最小深度
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
                if (!node->left && !node->right) { // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
            }
        }
        return depth;
    }

翻转二叉树

思路： 遍历的过程中翻转每一个节点的左右孩子就可以完成整体翻转
前序遍历，后序遍历，层序遍历都可以，但是中序遍历不可以，中序遍历可能会导致某些节点的左右孩子翻转两次

//前序遍历完成翻转
    //递归实现
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        swap(root->left, root->right);  // 中
        invertTree(root->left);         // 左
        invertTree(root->right);        // 右
        return root;
    }
    //迭代实现
    TreeNode* invertTree(TreeNode* root) {
        if (root == NULL) return root;
        stack<TreeNode*> st;
        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();              // 中
            st.pop();
            swap(node->left, node->right);
            if(node->right) st.push(node->right);   // 右
            if(node->left) st.push(node->left);     // 左
        }
        return root;
    }

//广度优先搜索 层序遍历实现翻转
  TreeNode* invertTree(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                swap(node->left, node->right); // 节点处理
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return root;
    }