[Luogu P3272] [BZOJ 2331] [SCOI2011]地板

洛谷传送门

BZOJ传送门

题目描述

lxhgww的小名叫”小L“，这是因为他总是很喜欢$L型$的东西。小L家的客厅是一个$R\ast C$的矩形，现在他想用$L$型的地板来铺满整个客厅，客厅里有些位置有柱子，不能铺地板。现在小L想知道，用$L$型的地板铺满整个客厅有多少种不同的方案？需要注意的是，如下图所示，$L$型地板的两端长度可以任意变化，但不能长度为$0$。

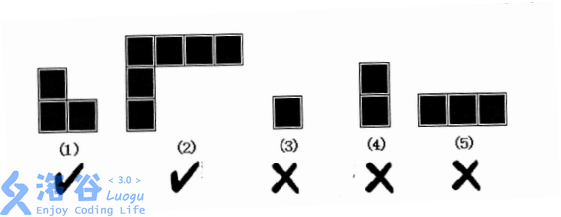
铺设完成后，客厅里面所有没有柱子的地方都必须铺上地板，但同一个地方不能被铺多次。

输入输出格式

输入格式：

输入的第一行包含两个整数，$R$和$C$，表示客厅的大小。接着是$R$行，每行$C$个字符。’_‘表示对应的位置是空的，必须铺地板；’*'表示对应的位置有柱子，不能铺地板。

输出格式：

输出一行，包含一个整数，表示铺满整个客厅的方案数。由于这个数可能很大，只需输出它除以$20110520$的余数。

输入输出样例

输入样例#1：

2 2
*_
__

输出样例#1：

1

输入样例#2：

3 3
 ___
 _*_
 ___

输出样例#2：

8

说明

测试点编号      数据范围             
1,2             R*C<=25
3-5             R*C<=100并且（R=2或者C=2）
6-10            R*C<=100

解题分析

一道奇奇怪怪的插头$DP$题。

我们要确定一个$L$形地板如何放置， 无非是关注其在哪里拐弯， 和向后延伸的方向。

因此我们规定$1$为未拐弯的$L$形的一半， $2$为已经拐过弯的插头， 并强制只能向右和向下延伸， 那么分类讨论转移就好了。

左右颠倒的$L$形可以通过向右和向下的$1$插头拼接得到。

代码如下：

#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <cctype>
#include <unordered_map>
#include <algorithm>
#define R register
#define IN inline
#define W while
#define gc getchar()
#define ll long long
#define MX 5000500
#define MOD 20110520
std::unordered_map <int, int> ind;
int stat[2][MX], dgt[15], tot[2], val[2][MX];
bool mp[105][105];
char buf[105][105];
int now, pre = 1, n, m, bdn, bdm, ans;
IN void insert(R int hs, R int v)
{
	R int pos = ind[hs];
	if (!pos) ind[hs] = pos = ++tot[now], stat[now][pos] = hs, val[now][pos] = v;
	else (val[now][pos] += v) %= MOD;
}
int main(void)
{
	int i, j, k, l, st, v, lef, up, base;
	scanf("%d%d", &n, &m);
	for (i = 1; i <= n; ++i) scanf("%s", buf[i] + 1);
	if (m > n)
	{
		for (i = 1; i <= n; ++i)
		for (j = 1; j <= m; ++j)
		mp[j][n - i + 1] = (buf[i][j] == '_');
		std::swap(n, m);
	}
	else
	{
		for (i = 1; i <= n; ++i)
		for (j = 1; j <= m; ++j)
		mp[i][j] = (buf[i][j] == '_');
	}
	for (i = 1; i <= m; ++i) dgt[i] = i << 1;
	for (i = 1; i <= n; ++i)
	for (j = 1; j <= m; ++j)
	if (mp[i][j]) bdn = i, bdm = j;
	tot[now] = 1; val[now][1] = 1;
	for (i = 1; i <= n; ++i)
	{
		for (j = 1; j <= m; ++j)
		{
			std::swap(now, pre);
			ind.clear(); tot[now] = 0;
			for (k = 1; k <= tot[pre]; ++k)
			{
				st = stat[pre][k], v = val[pre][k];
				lef = (st >> dgt[j - 1]) % 4, up = (st >> dgt[j]) % 4;
				base = st ^ (lef << dgt[j - 1]) ^ (up << dgt[j]);
				if (!mp[i][j]) {if (lef == 0 && up == 0) insert(base, v);}
				else
				{
					if (lef == 0)
					{
						if (up == 0)
						{
							if (mp[i + 1][j] && mp[i][j + 1]) insert(base | (2 << dgt[j - 1]) | (2 << dgt[j]), v);
							if (mp[i + 1][j]) insert(base | (1 << dgt[j - 1]), v);
							if (mp[i][j + 1]) insert(base | (1 << dgt[j]), v);
						}
						else if (up == 1)
						{
							if (mp[i + 1][j]) insert(base | (1 << dgt[j - 1]), v);
							if (mp[i][j + 1]) insert(base | (2 << dgt[j]), v);
						}
						else
						{
							if (mp[i + 1][j]) insert(base | (2 << dgt[j - 1]), v);
							insert(base, v);
							if (i == bdn && j == bdm) (ans += v) %= MOD;
						}
					}
					else if (lef == 1)
					{
						if (up == 0)
						{
							if (mp[i + 1][j]) insert(base | (2 << dgt[j - 1]), v);
							if (mp[i][j + 1]) insert(base | (1 << dgt[j]), v);
						}
						else if (up == 1)
						{
							insert(base, v);
							if (i == bdn && j == bdm && (!base)) (ans += v) %= MOD;
						}
					}
					else
					{
						if (up == 0)
						{
							if (mp[i][j + 1]) insert(base | (2 << dgt[j]), v);
							insert(base, v);
							if (i == bdn && j == bdm) (ans += v) %= MOD;
						}
					}
				}
			}
		}
		for (l = 1; l <= tot[now]; ++l) stat[now][l] <<= 2;
	}
	printf("%d", ans);
}