2018-2019 NEERC Finals M. Minegraphed

Codeforces传送门

Marika is developing a game called “Minegraphed” that involves moving around a $3D$ rectangular world.
Each cell of a parallelepiped game field is either an empty cell or an obstacle cell. You are always standing
inside an empty cell, located either in the bottommost layer or on top of an obstacle cell. Each move can
be made in one of four directions: north, east, south, or west. You make a move according to these rules:

• If you try to move outside of the parallelepiped, then you can’t make this move.
• Otherwise, if the cell in front of you is empty, then you move one cell forward and then fall towards
  the bottom until you reach the bottommost layer or an obstacle cell.
• Otherwise, if you are in non-topmost layer, the cell in front of you is an obstacle, the cell above you
  and the cell above that obstacle are both empty, then you move (climb up) on top of that obstacle.
• Otherwise, you can’t make this move.

Input

The first line contains a single integer $n(1\le n\le 9)$ — the number of vertices. Each of the next $n$ lines
contains $n$ integers equal to $0$ or $1$. The $j-th$ number in the $i-th$ line is $1$ if there is an edge from vertex $i$
to vertex $j$ and $0$ otherwise. The $i-th$ number in the $i-th$ line is always zero.

Output

Output a layer-by-layer description of a field that has the same reachability as the given graph.
The first line should contain three positive integers $x$, $y$, and $z$, the west-east, north-south, and top-bottom
sizes of the designed parallelepiped. Blocks describing $z$ layers should follow, from the topmost layer to
the bottommost layer, separated by single empty lines. Each block should contain $y$ lines of length $x$,
consisting of dots (‘.’), hashes (‘#’), and digits from $1$ to $n$. A hash denotes an obstacle cell. A dot denotes
an unlabeled empty cell. A digit denotes a labeled empty cell. Each digit from $1$ to $n$ should appear
exactly once. Each digit should be located either in the bottommost layer or on top of an obstacle cell. It
is okay for obstacles to be “hanging in the air” (there is no gravity for them).
The volume of the field $x\times y\times z$ should not exceed $10^6$. It is guaranteed that there is a correct field fitting into this limit for any possible graph in the input.

Example

Input

4
0 1 0 1
0 0 1 0
0 1 0 0
1 0 0 0

Output

4 2 3
..#.
.4..

####
1#.#

..3.
#2..

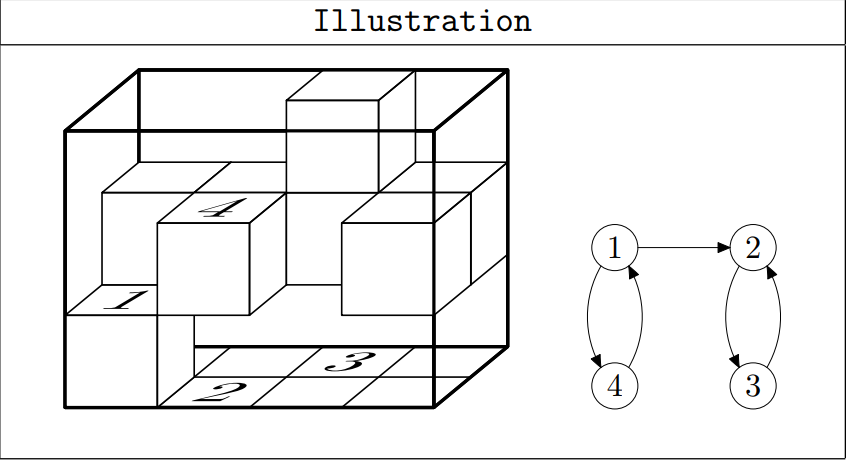
解题分析

题目数据本来可以出到$100$的…

显然， 对于原图， 我们进行一次tarjan后， 一个强连通分量里的所有点都可以互相到达， 而缩点后会出现一个$DAG$， 那么拓扑序小的点应该在三维图中比拓扑序大的点更靠上。

这里有一种很简单的做法： 我们暴力建一个高为$30$， 宽为$20$， 长为$20$的长方体出来， 先使它形成一层空、一层填满的状态， 然后利用拓扑序， 将在一个强连通分量里的点划分到一块去， 再向下逐个”挖洞“到其他强连通分量去。

具体实现细节很多， 见代码注释。

#include <bits/stdc++.h>
using namespace std;
#define R register
#define IN inline
#define W while
#define gc getchar()
#define MX 300
int n, ct, top, tot, cnt;
int bel[MX], mp[MX][MX], dfn[MX], low[MX], sta[MX], deg[MX], head[MX], layer[MX];
bool emp[31][105][105];
int res[31][105][105];
queue <int> q;
vector <int> vec[MX];
bool inq[MX];
struct Edge {int to, nex;} edge[MX << 1];
IN void add(R int from, R int to) {edge[++cnt] = {to, head[from]}, head[from] = cnt;}
void tarjan(R int now)
{
	dfn[now] = low[now] = ++ct;
	inq[now] = true;
	sta[++top] = now;
	for (R int i = 1; i <= n; ++i)
	{
		if (i == now || (!mp[now][i])) continue;
		if (!dfn[i]) tarjan(i), low[now] = min(low[now], low[i]);
		else if (inq[i]) low[now] = min(low[now], dfn[i]);
	}
	if (dfn[now] == low[now])
	{
		R int cur = 0; ++tot;
		W (cur ^ now)
		{
			cur = sta[top--];
			bel[cur] = tot;
			inq[cur] = false;
			vec[tot].push_back(cur);
		}
	}
}
int main()
{
	int cur = 29, pip = -1, now;
	scanf("%d", &n);
	for (R int i = 1; i <= n; ++i)
	for (R int j = 1; j <= n; ++j)
	scanf("%d", &mp[i][j]);
	for (R int i = 1; i <= n; ++i) if (!dfn[i]) tarjan(i);
	for (R int i = 1; i <= n; ++i)
	for (R int j = 1; j <= n; ++j)
	if (mp[i][j] && bel[i] != bel[j]) add(bel[i], bel[j]), deg[bel[j]]++;
	for (R int i = 1; i <= tot; ++i) if (!deg[i]) q.push(i), layer[i] = (cur -= 2);
	W (!q.empty())
	{
		now = q.front(); q.pop();
		for (R int i = 1; i <= 100; ++i)
		for (R int j = 1; j <= 100; ++j)
		res[layer[now]][i][j] = -1;//封住这一层作为地面
		for (R int i = 1; i <= 100; ++i) res[layer[now] + 1][2][i] = -1, res[layer[now] + 1][3][i] = -1, res[layer[now] + 1][4][i] = -1;//封住后三行
		for (R int i = 0; i < vec[now].size(); ++i)//向第一行塞数
		res[layer[now] + 1][1][i + 1] = vec[now][i];
		for (R int i = head[now]; i; i = edge[i].nex)
		{
			deg[edge[i].to]--;
			if (deg[edge[i].to]) continue;
			layer[edge[i].to] = (cur -= 2);//分配下一层
			q.push(edge[i].to);
		}
	}
	for (now = 1; now <= tot; ++now)
	{
		for (R int j = head[now]; j; j = edge[j].nex)
		{
			pip += 2;//分配管道位置， 不能相邻
			emp[layer[now] + 1][2][pip] = emp[layer[now] + 1][3][pip] = true;//打穿墙
			for (R int i = layer[now]; i > layer[edge[j].to]; --i) emp[i][3][pip] = true;//打穿地板
			emp[layer[edge[j].to] + 1][2][pip] = true;
		}
	}
	int aa = 100, bb = 100, cc = 30;
	printf("%d %d %d\n", aa, bb, cc);
	for (R int i = 30; i; --i)
	{
		for (R int j = 1; j <= 100; ++j)
		{
			for (R int k = 1; k <= 100; ++k)
			{
				if (emp[i][j][k] || (!res[i][j][k])) putchar('.');
				else if (res[i][j][k] == -1) putchar('#');
				else printf("%d", res[i][j][k]);
			}
			puts("");
		}
		puts("");
	}
}