[Luogu P3642] [BZOJ 4585] [APIO2016]烟火表演

最新推荐文章于 2022-11-13 18:45:59 发布

LPA20020220

最新推荐文章于 2022-11-13 18:45:59 发布

阅读量341

点赞数

CC 4.0 BY-SA版权

分类专栏：计算几何动态规划树形dp 数学堆文章标签：凸包 DP 动态规划数学

本文链接：https://blog.youkuaiyun.com/LPA20020220/article/details/80963948

动态规划同时被 3 个专栏收录

126 篇文章

订阅专栏

数学

122 篇文章

订阅专栏

树形dp

20 篇文章

订阅专栏

本博客探讨了在烟花表演中通过调整导火索长度实现所有烟花同时爆炸的问题，涉及导火索布局优化、代价计算及算法设计。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全，烟花被安置在远离开关的位置上，通过一些导火索与开关相连。导火索的连接方式形成一棵树，烟花是树叶，如图所示。火花从开关出发，沿导火索移动。每当火花抵达一个分叉点时，它会扩散到与之相连的所有导火索，继续燃烧。导火索燃烧的速度是一个固定常数。图中展示了六枚烟花 $\{E_1, E_2, \dots, E_6\}$ 的连线布局，以及每根导火索的长度。图中还标注了当在时刻 $0$ 从开关点燃火花时，每一发烟花的爆炸时间。

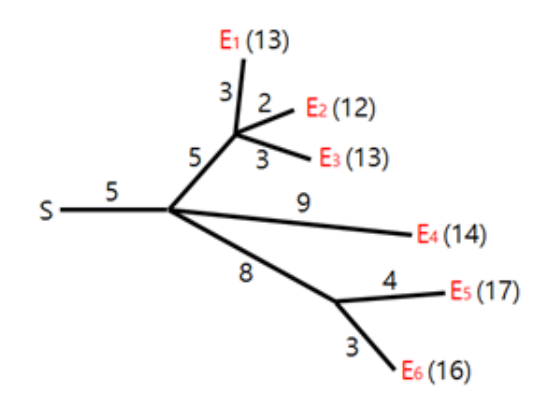
Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是，在他设计的布局中，烟花不一定同时爆炸。我们希望修改一些导火索的长度，让所有烟花在同一时刻爆炸。例如，为了让图中的所有烟花在时刻 $13$ 爆炸，我们可以像下图中左边那样调整导火索长度。类似地，为了让图中的所有烟花在时刻 $14$ 爆炸，我们可以像下图中右边那样调整长度。

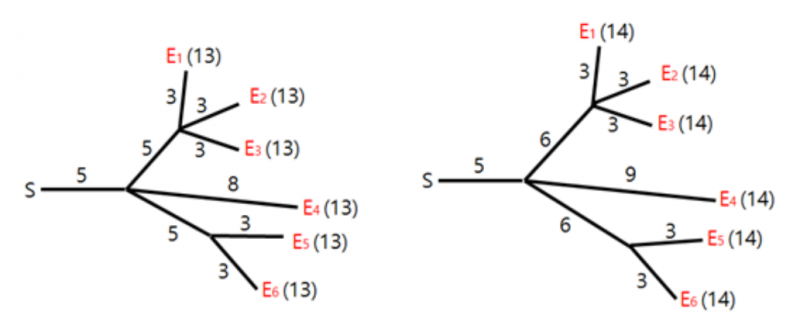
修改导火索长度的代价等于修改前后长度之差的绝对值。例如，将上面那副图中布局修改为下面那副图的左边布局的总代价为 $6$ ，而修改为右边布局的总代价为 $5$ 。

导火索的长度可以被减为 $0$ ，同时保持连通性不变。

给定一个导火索的连线布局，你需要编写一个程序，去调整导火索长度，让所有的烟花在同一时刻爆炸，并使得代价最小。

输入输出格式

输入格式：

所有的输入均为正整数。令 $N$ 代表分叉点的数量， $M$ 代表烟花的数量。分叉点从 $1$ 到 $N$ 编号，编号为 $1$ 的分叉点是开关。烟花从 $N + 1$ 到 $N + M$ 编号。

输入第一行为 $N, M$ 。后面 $N + M - 1$ 行，第 $i$ 行两个整数 $P_{i + 1}, C_{i + 1}$ 。其中 $P_i$ 满足 $1 \leq P_i < i$ ，代表和分叉点或烟花 $i$ 相连的分叉点。 $C_i$ 代表连接它们的导火索长度（ $1 \leq C_i \leq 10^9$ ）除开关外，每个分叉点和多于 $1$ 条导火索相连，而每发烟花恰好与 $1$ 条导火索相连。

输出格式：

输出调整导火索长度，让所有烟花同时爆炸，所需要的最小代价。

输入输出样例

输入样例#1：

输出样例#1：

说明

【数据规模】

子任务 1（7 分）： $N = 1$ , $1 \leq M \leq 100$ 。

子任务 2（19 分）： $1 \leq M \leq 300$ ，且开关到任一烟花的距离不超过 $300$ 。

子任务 3（29 分）： $1 \leq M \leq 5000$ 。

子任务 4（45 分）： $1 \leq M \leq 300000$ 。

解题分析

神题啊QAQ蒟蒻搞了好久才弄明白…

首先我们考虑 $f_A(x)$ 表示将 $A$ 点子树内所有烟火爆炸时间变为 $x$ 的花费，显然这是个下凸的函数，并且 $f_A(0)=\sum _{leaf_i\in subtree[A]}dis[i]$ 。

然后我们考虑从 $f_A(x)$ 转移到 $f_{fat[A]}(x)$ 的过程。设 $[L,R]$ 为 $f(x)$ 上最低的一段， $dis[A]$ 为 $A\to fat[A]$ 的长度， $f_A'(x)$ 为转移后的函数。

对于 $x\in [0,L]$ ，显然我们要将新的导火索清零，所以这一段函数向上平移 $dis[A]$ ，即 $f_A'(x)=f_A(x)+dis[A]$ 。
对于 $x\in [L+1,L+dis[A]-1]$ ，我们可以不修改以前的导火索，只减短新的导火索的长度。 $f'_A(x)=f_A(x)+dis[A]-(x-L)$ 。
对于 $x\in [L+dis[A],R+dis[A]]$ ，这一截就是原来的 $[L,R]$ 转移过来的，所以 $f'_A(x)=f_A(L)$ 。
对于 $x\in [R+dis[A]+1,+∞)$ ，我们可以加长新的导火索的长度，所以 $f'_A(x)=f_A(R)+x-(R+dis[A])$

也就是说大概是这个样子(dis[A]=2的情况)：

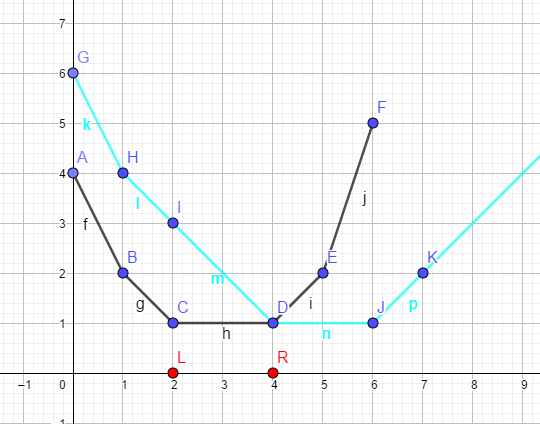
可以发现其实就是把 $f_A(x)$ 斜率非负的一半砍掉，另一半向上平移，再加入斜率为 $-1,0,1$ 的三段直线。

考虑如何合并几个凸包的 $f'(x)$ 从而得到 $f_{fat[A]}(x)$ 。大概就像下面这样：

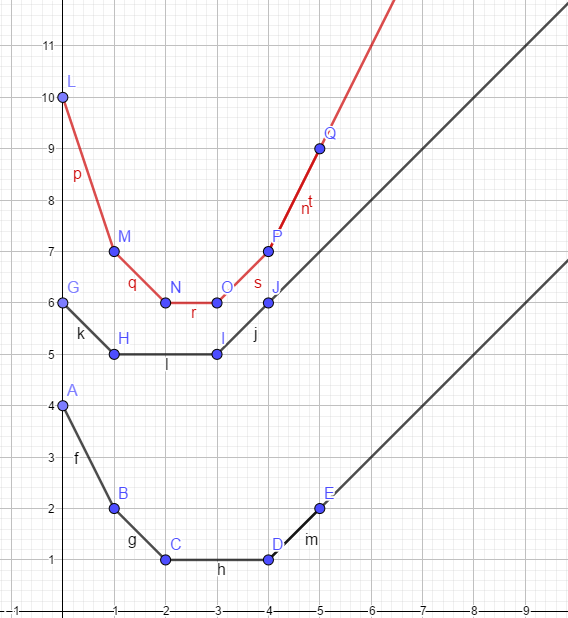
然后我们可以发现，对于合并后的凸包，每个原来的节点都会使斜率 $+1$ （其实上图的 $A\to B \to C\to D\to E$ 这个凸包的 $B$ 点少画了一个重合的点）。所以我们用一个可并堆直接暴力合并子树中的凸包。

那么如何得到合并后凸包的最小值？我们可以发现合并后的凸包的斜率为正部分的点数就是子树的个数，所以直接弹出 $son[fat[A]]$ 次即可。

但这样处理后我们只得到了 $[L,R]$ 区间，并没有得到对应的花费。这时有一个更妙妙的性质：因为每个点都会使凸包斜率+1，所以考虑一个在 $x_i$ 位置的点，其对花费的贡献是 $-x_i$ ，所以我们一边弹堆一边用总路径和（即为 $f_1(x)$ ）减去堆顶的元素。

（如果还有不太懂的同学可以画画图演示，博主反正是画图才懂QAQ）

下面是~~极其简短的~~代码（pb_ds大法好）

#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cctype>
#include <cmath>
#include <cstring>
#include <ext/pb_ds/priority_queue.hpp>
#define R register
#define IN inline
#define gc getchar()
#define W while
#define MX 300050
#define ll long long
template <class T>
IN void in(T &x)
{
    x = 0; R char c = gc;
    W (!isdigit(c)) c = gc;
    W (isdigit(c))
    x = (x << 1) + (x << 3) + c - 48, c = gc;
}
__gnu_pbds::priority_queue <ll> que[MX];
int son[MX], fat[MX], dis[MX], rop, fir;
ll sum;
int main(void)
{
    ll lef, rig;
    in(rop), in(fir); int bd = rop + fir;
    for (R int i = 2; i <= bd; ++i)
    {
        in(fat[i]), in(dis[i]);
        son[fat[i]]++; sum += dis[i];
    }
    for (R int i = bd; i >= 2; --i)
    {
        lef = rig = 0;
        if(i <= rop)
        {
            W (--son[i]) que[i].pop();
            lef = que[i].top(), que[i].pop();
            rig = que[i].top(), que[i].pop();
        }
        que[i].push(lef + dis[i]), que[i].push(rig + dis[i]);
        que[fat[i]].join(que[i]);//配对堆骚操作，直接合并
    }
    W (son[1]--) que[1].pop();
    W (!que[1].empty()) sum -= que[1].top(), que[1].pop();
    printf("%lld", sum);
}