547. 省份数量

题目

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

返回矩阵中 省份 的数量。

示例 1：

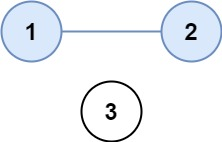
输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]]
输出：2

示例 2：

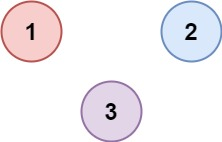
输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]]
输出：3

提示：

• 1 <= n <= 200
• n == isConnected.length
• n == isConnected[i].length
• isConnected[i][j] 为 1 或 0
• isConnected[i][i] == 1
• isConnected[i][j] == isConnected[j][i]

官方题解

方法一：深度优先搜索

深度优先搜索的思路是很直观的。遍历所有城市，对于每个城市，如果该城市尚未被访问过，则从该城市开始深度优先搜索，通过矩阵 isConnected 得到与该城市直接相连的城市有哪些，这些城市和该城市属于同一个连通分量，然后对这些城市继续深度优先搜索，直到同一个连通分量的所有城市都被访问到，即可得到一个省份。遍历完全部城市以后，即可得到连通分量的总数，即省份的总数。

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int provinces = isConnected.length;
        boolean[] visited = new boolean[provinces];
        int circles = 0;
        for (int i = 0; i < provinces; i++) {
            if (!visited[i]) {
                dfs(isConnected, visited, provinces, i);
                circles++;
            }
        }
        return circles;
    }

    public void dfs(int[][] isConnected, boolean[] visited, int provinces, int i) {
        for (int j = 0; j < provinces; j++) {
            if (isConnected[i][j] == 1 && !visited[j]) {
                visited[j] = true;
                dfs(isConnected, visited, provinces, j);
            }
        }
    }
}

方法二：广度优先搜索

也可以通过广度优先搜索的方法得到省份的总数。对于每个城市，如果该城市尚未被访问过，则从该城市开始广度优先搜索，直到同一个连通分量中的所有城市都被访问到，即可得到一个省份。

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int provinces = isConnected.length;
        boolean[] visited = new boolean[provinces];
        int circles = 0;
        Queue<Integer> queue = new LinkedList<Integer>();
        for (int i = 0; i < provinces; i++) {
            if (!visited[i]) {
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int j = queue.poll();
                    visited[j] = true;
                    for (int k = 0; k < provinces; k++) {
                        if (isConnected[j][k] == 1 && !visited[k]) {
                            queue.offer(k);
                        }
                    }
                }
                circles++;
            }
        }
        return circles;
    }
}

方法三：并查集

计算连通分量数的另一个方法是使用并查集。初始时，每个城市都属于不同的连通分量。遍历矩阵 isConnected，如果两个城市之间有相连关系，则它们属于同一个连通分量，对它们进行合并。

遍历矩阵 isConnected 的全部元素之后，计算连通分量的总数，即为省份的总数。

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int provinces = isConnected.length;
        int[] parent = new int[provinces];
        for (int i = 0; i < provinces; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < provinces; i++) {
            for (int j = i + 1; j < provinces; j++) {
                if (isConnected[i][j] == 1) {
                    union(parent, i, j);
                }
            }
        }
        int circles = 0;
        for (int i = 0; i < provinces; i++) {
            if (parent[i] == i) {
                circles++;
            }
        }
        return circles;
    }

    public void union(int[] parent, int index1, int index2) {
        parent[find(parent, index1)] = find(parent, index2);
    }

    public int find(int[] parent, int index) {
        if (parent[index] != index) {
            parent[index] = find(parent, parent[index]);
        }
        return parent[index];
    }
}

boolean[] visited = new boolean[provinces]
意思是创建布尔类型的数组，这个布尔类型数组的长度是provinces.
学到了学到了。

用到了二维数组，二维数组我还不太懂。去学习一下。

博客：https://blog.youkuaiyun.com/weixin_36564655/article/details/79615479

二维数组其实是一位数组的嵌套（每一行看做一个内层的一维数组）

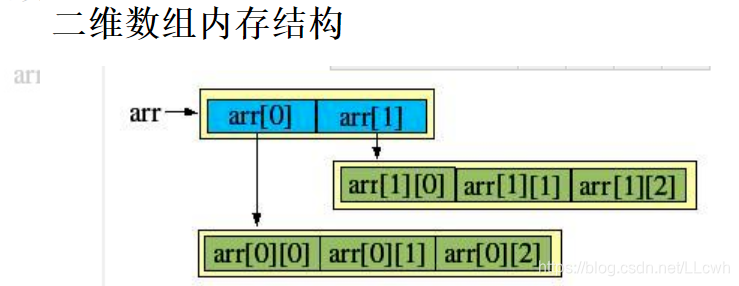
格式1: 动态初始化

数据类型 数组名 [ ][ ] = new 数据类型[m][n]
数据类型 [ ][ ]  数组名 = new 数据类型[m][n]
数据类型 [ ]   数组名 [ ] = new 数据类型[m][n]

举例：

int [ ][ ]  arr=new  int [5][3];  也可以理解为“5行3例”

格式2: 静态初始化

数据类型 [ ][ ]   数组名 = {{元素1,元素2....},{元素1,元素2....},{元素1,元素2....}.....};

举例：

int [ ][ ]  arr={{22,15,32,20,18},{12,21,25,19,33},{14,58,34,24,66},};

静态初始化可用于不规则二维数组的初始化

public static void main(String[]args){
		int [][] arr=new int[][]{{4,5,6,8},{2,3},{1,6,9}};
 
		System.out.println(arr.length);//输出行数
		System.out.println(arr[0].length);//输出列数	
	}

输出结果：
3
4

总结：有很多知识点还不会，也没有思路。方法也不熟练。总的来说有点懵。