Java 实现二叉树的基本操作

目录

回顾: 

二叉树的基本操作 ：

1.获取树中的节点

❌写法 

✅写法（2） 

递归展开 

2.获取叶子节点的个数

✅写法

递归展开 

3. 获取第K层节点的个数

思路

递归展开 

4. 获取树的深度

思路

✅写法 

递归展开 

5. 检测值为 val 的元素是否存在

思路

✅写法 

 递归展开

6.判断完全二叉树

思路

---

回顾: 

上篇学习了

二叉树的核心操作
把所有的节点，按一定的次序，全部访问（针对这个数据，进行各种操作如：打印，修改，判定，计算......）一遍，访问过程中“不重不漏”。二叉树的4种遍历方式：先序，中序，后序，层序
前三者都是基于递归实现的：为了方便理解给出了其各的递归展开图，本片也会借助图像为大家展现代码执行过程，方便理解方法实现。

二叉树的基本操作 ：

1. int size ( Node root ) ;	获取树中的节点
2. int getLeafNode( Node root );	获取叶子节点的个数
3. int getKLevelNodeCount ( Node root , int k);	获取第K层节点的个数
4. int getHeight ( Node root );	获取树的深度
5. Node find ( Node root, int val );	检测值为 val 的元素是否存在
6. boolean isCompleteTree ( Node root );	判断完全二叉树

 

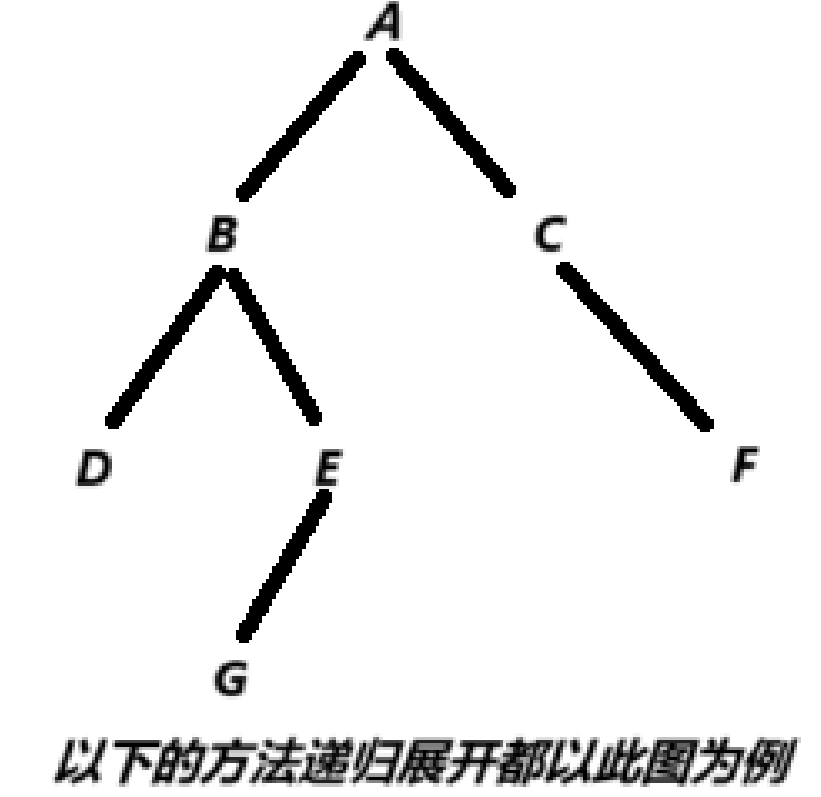
1.获取树中的节点

一棵树的个数：
根的个数（非空即为1）+ 左子树的节点个数 + 右子树的个数

❌写法 

   // 获取节点个数
    public static int size (Node root){
        // 遍历  先、中、后、层都可以
        if(root == null){
            return 0;
        }
        int size = 0;
        size++;
        size(root.left);
        size(root.right);
        return size;
    }

int size = 0;        局部变量，每次递归时，在对应的函数栈帧中都会有一个全新的size 变量；

解决方案 1. 将size 改为成员变量 public static int size = 0;

                2. 递归过程中，通过返回值把当前子树的递归结果返回到上层方法，上层方法再                        进行累加

✅写法（2） 

public static int size (Node root){
        // 遍历  先、中、后、层都可以
        if(root == null){
            return 0;
        }
        int rootSize = 1;
        int leftSize = size(root.left);
        int rightSize = size(root.right);
        return rootSize + leftSize + rightSize;
    }


// 简化
public static int size (Node root){
        // 遍历  先、中、后、层都可以
        if(root == null){
            return 0;
        }
        return rootSize + size(root.left) + size(root.right);
    }

递归展开 

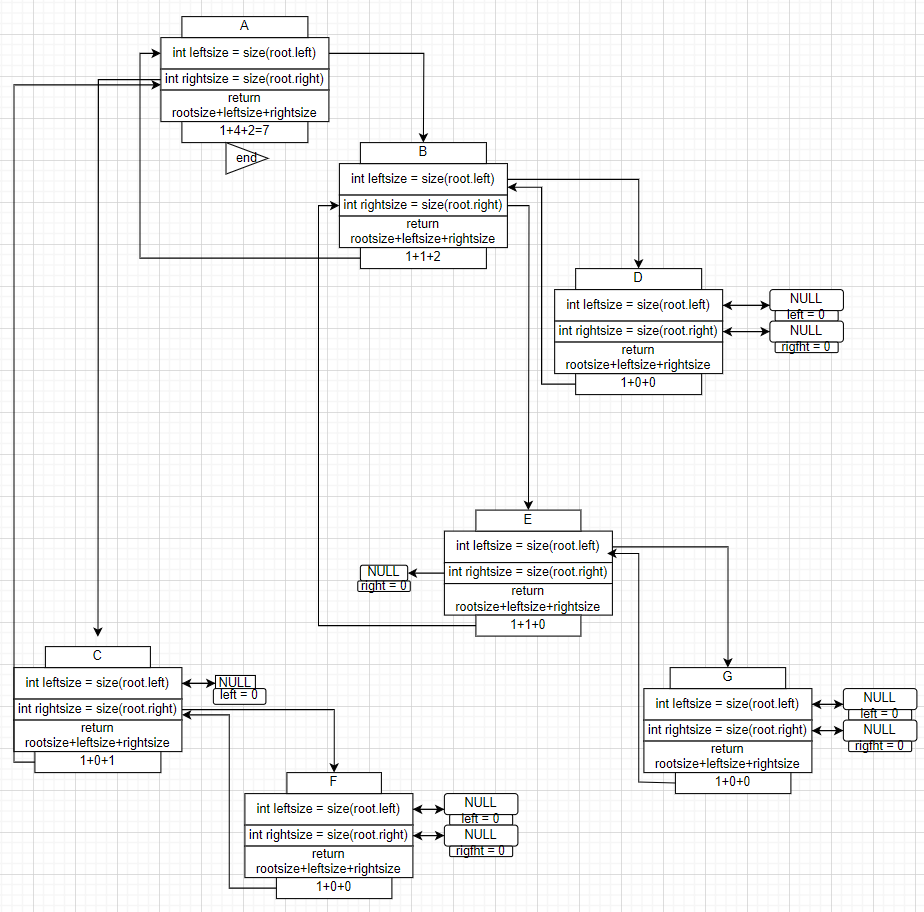
2.获取叶子节点的个数

叶子节点个数 = 左子树的叶子节点个数 + 右子树的叶子节点个数

✅写法

// 获取叶子节点个数
    public static int getLeafSize(Node root){
        if(root == null){
            return 0;
        }
        // 判定当前根节点是否是叶子
        if(root.left == null && root.right == null){
            return 1;
        }
        // 如果当前根节点不是叶子，分别求左右子树的叶子节点个数，再作和
        return getLeafSize(root.left) + getLeafSize(root.right);
    }

递归展开 

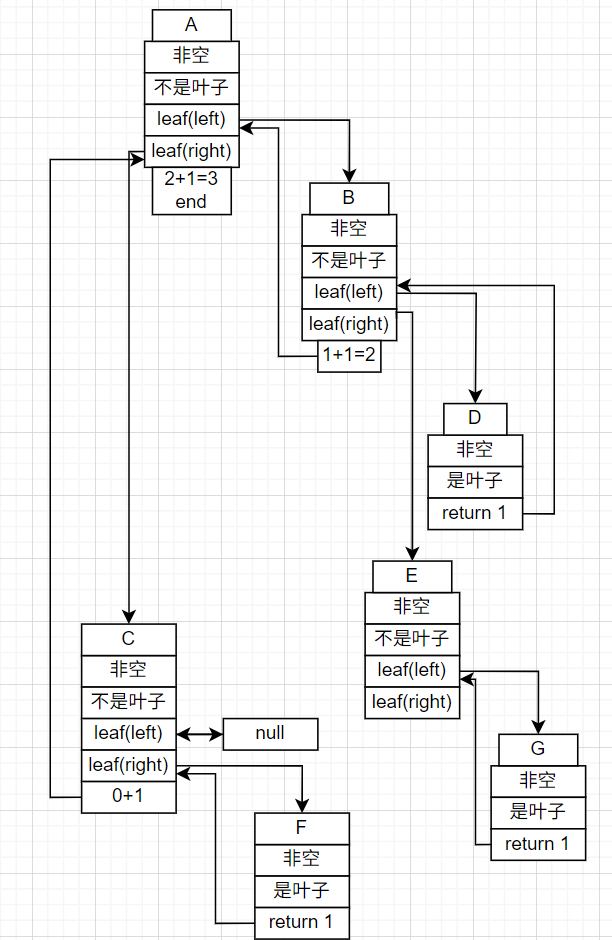
3. 获取第K层节点的个数

在二叉树的性质中：我们知道 k层树的节点个数最多有 2^(k-1)
此处要注意不能将获取第K层节点的个数和其混为一谈

思路

若 k < 1    非法
若 k = 1    求第一层节点个数                若是非空的树的，节点个数就是1

若 k > 1    求第k层节点个数     ——> 求左子树k-1层的节点个数  + 求右子树k-1层的节点个数

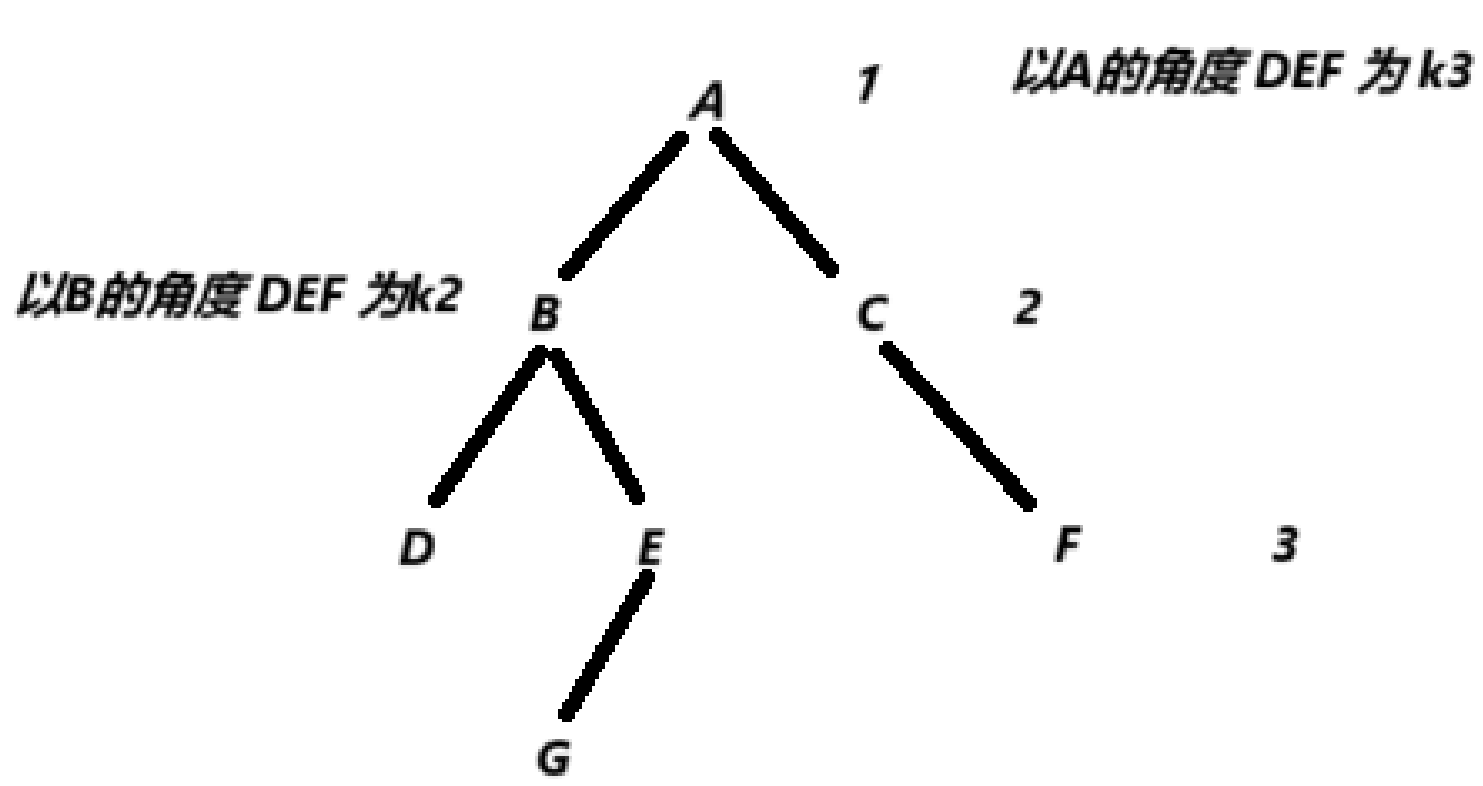
针对这个树 求k为3的节点个数
此问题等价于  求 B 这个子树的k 为2的节点个数 + C这个子树的k为2的节点个数
以B的视角：求 B 这个子树的k 为2的节点个数  =  求 D 这个子树的k 为1的节点个数 + E这个子树的k为1的节点个数

✅写法

 // 获取第k层节点个数
    public static int getKLevelNodeCount(Node root,int k){
        if(root == null || k < 1){
            return 0;
        }
        if(k == 1){
            // 对于非空的树来说 k==1 表示根节点
            return 1;
        }
        return getKLevelNodeCount(root.left,k-1) + getKLevelNodeCount(root.right,k-1);
    }

递归展开 

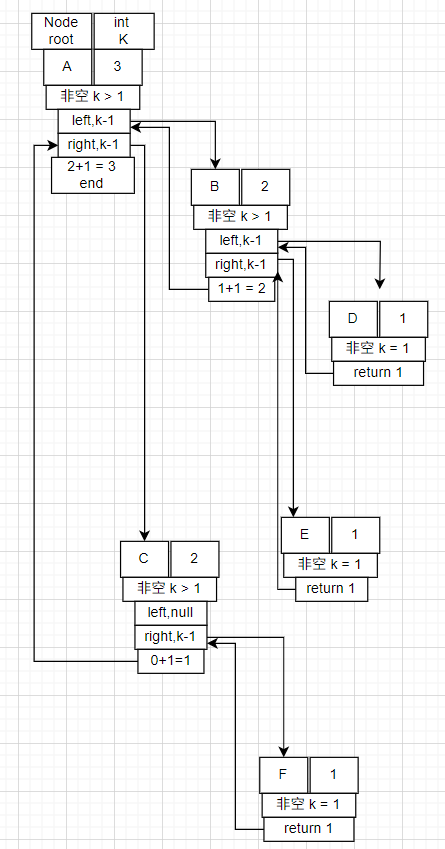
4. 获取树的深度

根节点出发到任意节点，路径的最大长度

思路

max(左子树的高度 ， 右子树的高度) + 1

✅写法 

    public static int getHeight(Node root){
        // 当前树的高度 = max( 左子树的高度 ， 右子树的高度 ） + 1
        if(root == null){
            return 0;
        }
        int leftHeight = getHeight(root.left);
        int rightHeight = getHeight(root.right);
        return Math.max(leftHeight,rightHeight) + 1;
       // return leftHeight > rightHeight ?  leftHeight + 1 : rightHeight + 1; 
//        if(leftHeight > rightHeight){
//            return leftHeight + 1;
//        }else{
//            return rightHeight + 1;
//        }
    }

后面两种写法也可以，但三目运算符 要注意运算优先级

递归展开 

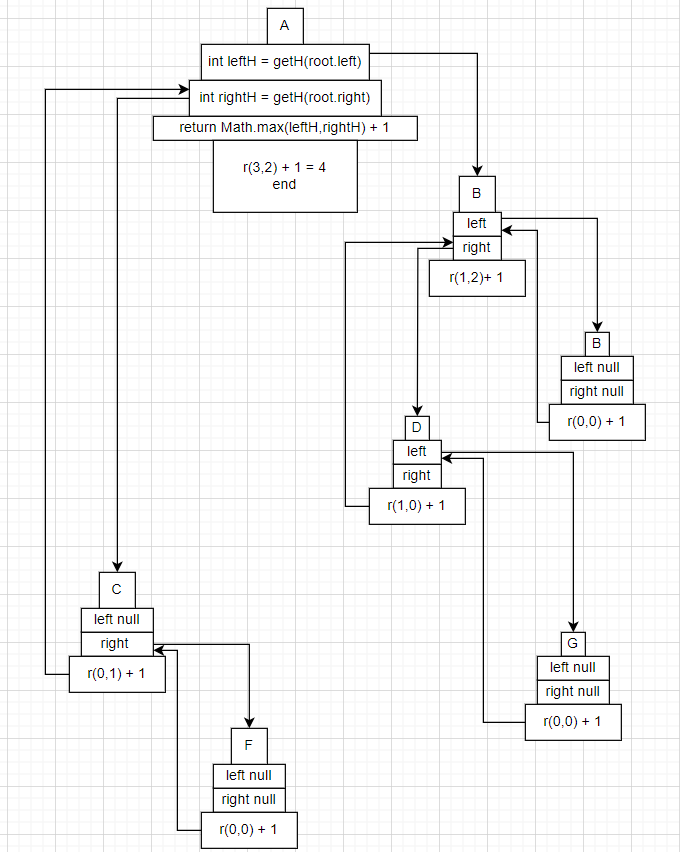
5. 检测值为 val 的元素是否存在

思路

判断跟节点是不是
      是，返回根节点
      不是，继续递归左子树找
如果也没找到
       递归右子树找

✅写法 

   // 查找val是否存在
    public static  Node find(Node root,String val){
        if(root == null){
            return null;
        }
        if(root.val.equals(val)){
            return root;
        }
        Node leftRes = find(root.left,val);
        if(leftRes != null){
            //找到了直接返回上述结果
            return leftRes;
        }
        //没找到，继续在右子树中找
        return find(root.right,val);
    }

 递归展开

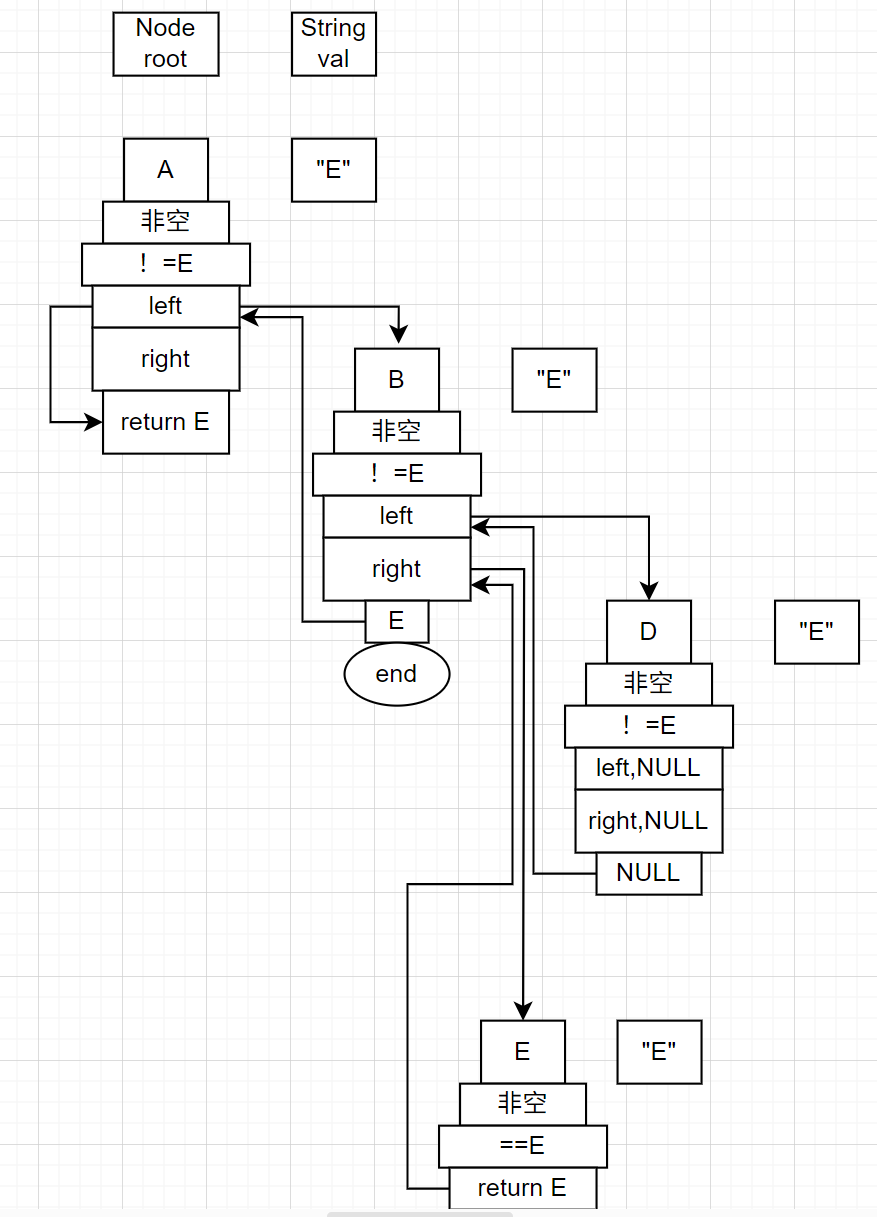
6.判断完全二叉树

思路

1.要求每个节点必须有两个子树
      a ) 没有子树     进入二阶段
      b）只有左子树 进入二阶段
      c ) 只有右子树    false
2.要求每个节点必须没有子树

  

   public static boolean isComplete(Node root) {
    if (root == null) {
        return true; // 空树是完全二叉树
    }
    
    boolean isFirstStage = true;
    Queue<Node> queue = new LinkedList<>();
    queue.offer(root);
    
    while (!queue.isEmpty()) {
        Node current = queue.poll();
        
        if (isFirstStage) {
            if (current.left == null && current.right == null) {
                isFirstStage = false; // 进入第二阶段
            } else if (current.left != null && current.right == null) {
                isFirstStage = false; // 只有左子树，进入第二阶段
                queue.offer(current.left); // 别忘了处理左子树
            } else if (current.left == null && current.right != null) {
                return false; // 只有右子树，违反完全二叉树规则
            } else {
                // 左右子树都有，继续正常遍历
                queue.offer(current.left);
                queue.offer(current.right);
            }
        } else {
            // 第二阶段：所有节点必须无子节点
            if (current.left != null || current.right != null) {
                return false;
            }
        }
    }
    
    return true; // 遍历完所有节点都符合条件
}

整条街都是恋爱的人    我独自走在暖风的夜

——寂寞的季节 DT

🌟💗🦀