栈的练习（有效的括号&最小栈）-java

接上篇  Java中栈 栈的练习 

🌟合适的括号

题目来源：leetCode  有效的括号

 返回 false 的情况 
1. 左右括号不匹配  如 [ } (} [) 等等
2. 出现独狼 存在找不到匹配对象的括号  
    左括号多余/ 有括号多余

解题思路：如图示例

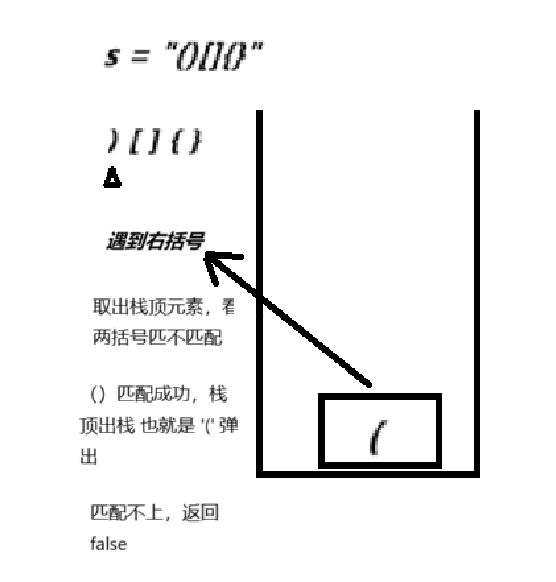
字符串 s = "() [] {}"

1. 创建一个栈来存放左括号 ‘(’  ‘[’  ‘}’
2. 遍历字符串如果当前字符是  ‘(’ 或 ‘[’ 或 ‘}’ 的左括号 将其入栈
3. 是右括号，取出栈顶元素，判定是否匹配 （匹配继续遍历，反之返回 false）
4. 遍历结束，判定栈是否为空（为空则全部匹配成功，反之有独狼未匹配成功）

♣️代码实现 

class Solution {
    public boolean isValid(String s) {
        //1. 准备栈，遍历字符串的每个字符
        //2. 如果发现当前字符是左括号，就直接入栈
        //3. 如果发现当前字符是右括号，取出刚才的栈顶元素，用当前的右括号和栈顶左括号去判定匹配  ） 和 （    ] 和 [   } 和 {
            // 配对就继续往下遍历
            // 不配对就返回 false
        Stack<Character> stack = new Stack<>();
        for(int i = 0; i < s.length(); i++){
            char c = s.charAt(i);
            // 如果是左括号 入栈
            if(c == '(' || c == '[' || c == '{'){   // 包装类自动拆箱转为内置类 可以使用 == 
                stack.push(c);
                continue;
            }
            // 右括号 判断匹配
            if(c == ')' || c == ']' || c == '}'){
                //取出刚才的栈顶元素
                if(stack.isEmpty()){
                    // 为空 又读到了右括号
                    return false;
                }
                char top = stack.pop();
                if(top == '(' && c == ')'){
                    // 情况一 ， 匹配成功
                    continue;
                }
                if(top == '[' && c == ']'){
                    // 情况二 ， 匹配成功
                    continue;
                }
                if(top == '{' && c == '}'){
                    // 情况三 ， 匹配成功
                    continue;
                }
                return false;
            }
        }
        // 整个循环结束，判断栈是否为空
        // 如果栈为空，说明所有括号都匹配成功
        // 不为空，说明还有未匹配的左括号
        if(stack.isEmpty()){
            return true;
        }
        return false;
    }
}

最小栈

题目来源: leetCode 最小栈​ 

直接的想法：可不可以把栈遍历一遍去找出最小值?

当然这种方式直接明了容易想到：

public int getMin() {

        if (stack.isEmpty()) {

            return 0;

        }

        int min = stack.peek();

        for (int num : stack) {

            if (num < min) {

                min = num;

            }

        }

        return min;

    }

// stack 为创建的栈来存元素，通过遍历其中元素找最小值

这种方法的缺点明显：

执行一次 getMin()方法都需要遍历一遍栈，时间复杂度为 O(N)，效率相对使用一个辅助栈的双栈法要低。

那么双栈法怎么理解：

 

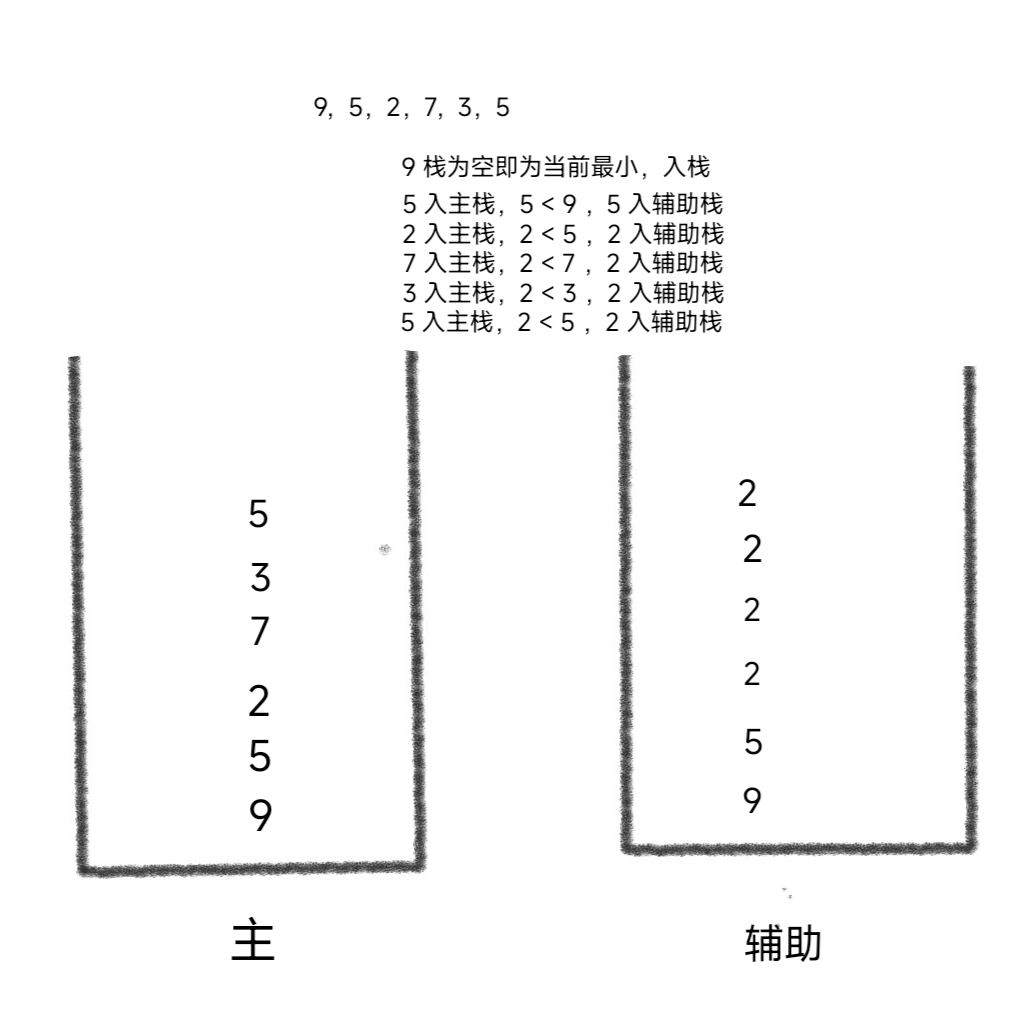
如上图，我们把元素正常压入主栈中，将元素与辅助栈栈顶元素相比，找出最小值压入辅助栈，这样可以确保辅助栈顶始终是当前主栈元素中最小值。

时间复杂度: O(1)

♦️代码实现 

class MinStack {
    private Stack<Integer> stack1 = new Stack<>();
    private Stack<Integer> stack2 = new Stack<>();

    public MinStack() {
        // 空着就行  上面声明变量创建对象的时候初始化过了
    }
    
    public void push(int val) {
        // stack1 正常入栈
        stack1.push(val);
        // stack2 
        if(stack2.isEmpty()){
            stack2.push(val);
            return;
        }
        int min = stack2.peek();
        if(val < min){
            stack2.push(val);
        }else{
            stack2.push(min);
        }
    }
    
    public void pop() {
        if(stack1.isEmpty()){
            return;
        }
        stack1.pop();
        stack2.pop();
    }
    
    public int top() {
        if(stack1.isEmpty()){
            return 0;
        }
        return stack1.peek();
    }
    
    public int getMin() {
        if(stack2.isEmpty()){
            return 0;
        }
        return stack2.peek();
    }
}

每次一想到你 像雨过天晴，看见一只蝴蝶飞过废墟，是那么的美丽，就像一个奇迹   

--蝴蝶 Dt

⭐️🌟🌟🌟🌟

欢迎评论