克鲁斯卡尔（Kruskal）算法求最小生成树

• 算法思想：贪心算法，先将图的所有点存起来，然后每次找出该图中权最小的边，如果该边加入到已经生成的树中不会形成回路就可以加入，否则不行，直到边数等于顶点数减一时停止加边进去

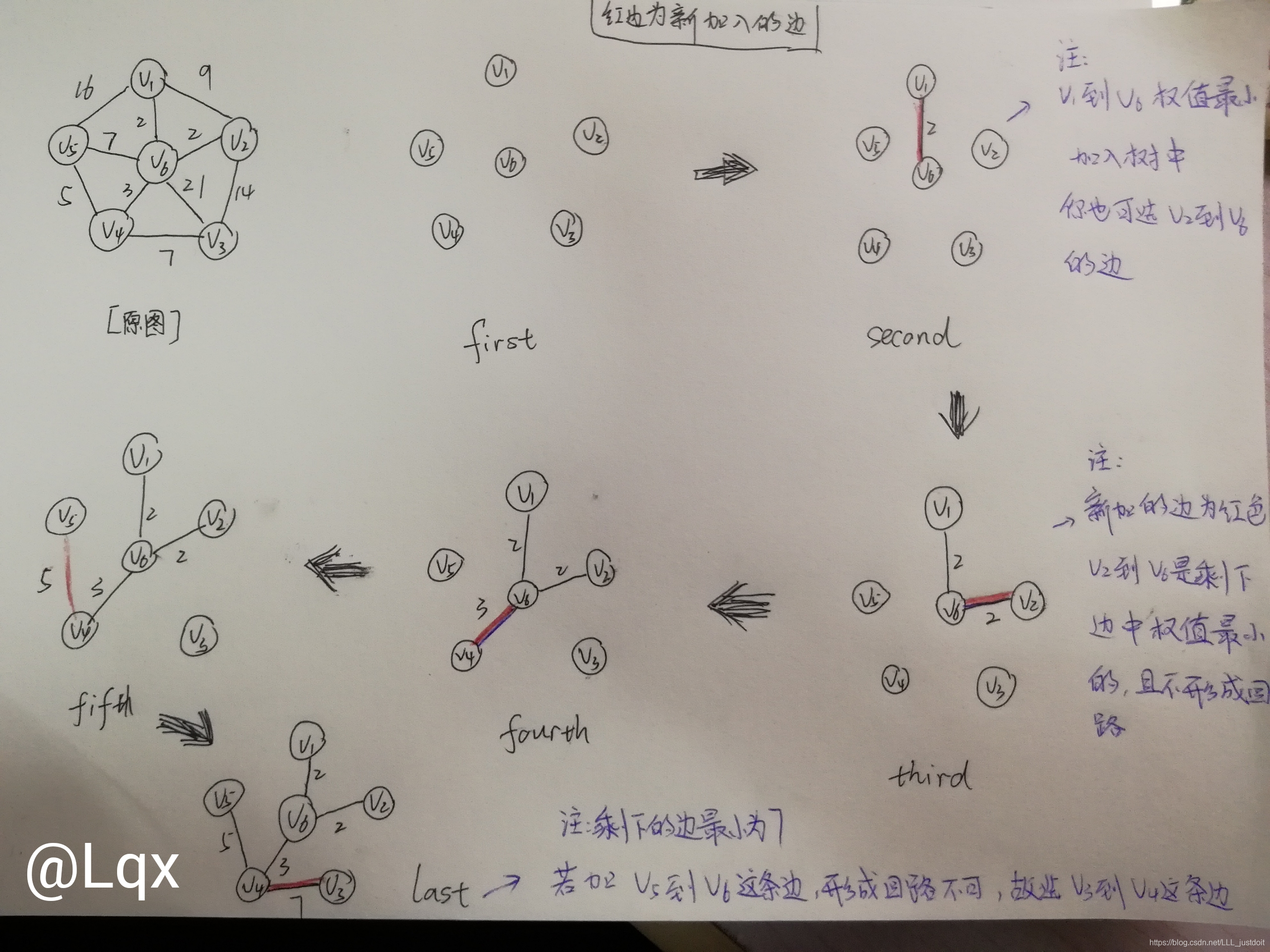
• 下图是kruskal算法的图解

• 

• 上代码,注意要判断是否形成回路，这是该算法的核心

  /*
   * 类描述：克鲁斯卡尔算法求最小生成树
   * @author Lqx
   */
  public class Kruskal {
  	public static final int M = -1;
  	// 建图(用二维矩阵存储图)
  	static int[][] map = { 
  			{ M, 9, M, M, 16, 2 }, 
  			{ 9, M, 14, M, M, 2 }, 
  			{ M, 14, M, 7, M, 21 },
  			{ M,  M, 7, M, 5, 3 },
  			{ 16, M, M, 5, M, 7 }, 
  			{ 2, 2, 21, 3, 7, M } 
  			};
  	static int[][] tree = new int[map.length][map.length]; //存放最小生成树
  	/*
  	 * 方法描述：该方法用于求最小生成树
  	 * @param a:待求的图
       * @author Lqx
  	 */
  	static int[][] kruskal(int[][] a) {
  
  		int vexnumber = a.length;
  		int begin = 0; // 存放起点下标
  		int tempmin = -1; //暂时存放最小边
  		int