基于DES和RSA算法自动分配密钥的加密聊天程序

---

实现的功能

（1）实现基于DES和RSA算法的自动分配密钥加密聊天程序。

（2）实现密钥自动生成，并基于RSA算法进行密钥共享。

（3）实现基于DES加密的全双工通信，并且加密过程对用户是透明的。

---

一、安全加密模型

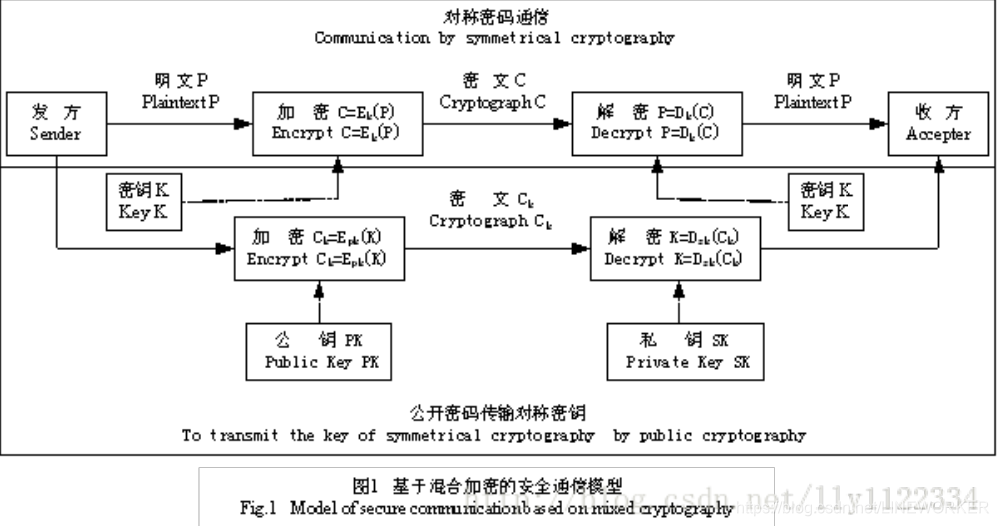
在这个模型中 E()代表加密，D()代表解密，我们要的是发方与收方之间的加密通信，这个加密通信是基于DES加密的，DES加密是对称加密（收发两方使用的秘钥相同），发方会产生DES秘钥，但是DES秘钥要怎么传递给收方呢？ 这就要用到RSA非对称加密，直白的说，使用RSA加密就是加密的发放的秘钥。
RSA是非对称加密，发方使用收方的公钥加密自己的DES秘钥，然后传递给收方，收方再用自己的RSA私钥进行解密，获得DES秘钥。

二、代码

DES_BOX.py

# !/usr/bin/python3
# 说明:  DES中用到的盒

IP_table = [58, 50, 42, 34, 26, 18, 10, 2,
            60, 52, 44, 36, 28, 20, 12, 4,
            62, 54, 46, 38, 30, 22, 14, 6,
            64, 56, 48, 40, 32, 24, 16, 8,
            57, 49, 41, 33, 25, 17, 9, 1,
            59, 51, 43, 35, 27, 19, 11, 3,
            61, 53, 45, 37, 29, 21, 13, 5,
            63, 55, 47, 39, 31, 23, 15, 7]


IP_re_table = [40,8, 48, 16, 56, 24, 64, 32, 39,
             7, 47, 15, 55, 23, 63, 31, 38, 6,
             46, 14, 54, 22, 62, 30, 37,5, 45,
             13, 53, 21, 61, 29, 36, 4, 44, 12,
             52, 20, 60, 28, 35, 3, 43, 11, 51,
             19, 59, 27, 34, 2, 42, 10, 50, 18,
             58, 26, 33, 1, 41,9, 49, 17, 57, 25]




E  = [32, 1,  2,  3,  4,  5,  4,  5,
       6, 7,  8,  9,  8,  9, 10, 11,
      12,13, 12, 13, 14, 15, 16, 17,
      16,17, 18, 19, 20, 21, 20, 21,
      22, 23, 24, 25,24, 25, 26, 27,
      28, 29,28, 29, 30, 31, 32,  1]



P = [16,  7, 20, 21, 29, 12, 28, 17,
     1, 15, 23, 26,  5, 18, 31, 10,
     2,  8, 24, 14, 32, 27,  3,  9,
     19, 13, 30, 6, 22, 11,  4,  25]


S =  [
 [14, 4, 13,  1,  2, 15, 11,  8,  3, 10,  6, 12,  5,  9,  0,  7,
     0, 15,  7,  4, 14,  2, 13,  1, 10,  6, 12, 11,  9,  5,  3,  8,
     4,  1, 14,  8, 13,  6,  2, 11, 15, 12,  9,  7,  3, 10,  5,  0,
     15, 12,  8,  2,  4,  9,  1,  7,  5, 11,  3, 14, 10,  0,  6, 13 ],



[15,  1,  8, 14,  6, 11,  3,  4,  9,  7,  2, 13, 12,  0,  5, 10,
     3, 13,  4,  7, 15,  2,  8, 14, 12,  0,  1, 10,  6,  9, 11,  5,
     0, 14,  7, 11, 10,  4, 13,  1,  5,  8, 12,  6,  9,  3,  2, 15,
     13,  8, 10,  1,  3, 15,  4,  2, 11,  6,  7, 12,  0,  5, 14,  9],


[10,  0,  9, 14,  6,  3, 15,  5,  1, 13, 12,  7, 11,  4,  2,  8,
     13,  7,  0,  9,  3,  4,  6, 10,  2,  8,  5, 14, 12, 11, 15,  1,
     13,  6,  4,  9,  8, 15,  3,  0, 11,  1,  2, 12,  5, 10, 14,  7,
     1, 10, 13,  0,  6,  9,  8,  7,  4, 15, 14,  3, 11,  5,  2, 12 ],


[7, 13, 14,  3,  0,  6,  9, 10,  1,  2,  8,  5, 11,  12,  4, 15,
     13,  8, 11,  5,  6, 15,  0,  3,  4,  7,  2, 12,  1, 10, 14,9,
     10,  6,  9,  0, 12, 11,  7, 13, 15,  1,  3, 14,  5,  2,  8,  4,
     3, 15,  0,  6, 10,  1, 13,  8,  9,  4,  5, 11, 12,  7,  2, 14],


 [2, 12,  4,  1,  7, 10, 11,  6,  8,  5,  3, 15, 13,  0, 14,  9,
     14, 11,  2, 12,  4,  7, 13,  1,  5,  0, 15, 10,  3,  9,  8,  6,
     4,  2,  1, 11, 10, 13,  7,  8, 15,  9, 12,  5,  6,  3,  0, 14,
     11,  8, 12,  7,  1, 14,  2, 13,  6, 15,  0,  9, 10,  4,  5,  3],

[12,  1, 10, 15,  9,  2,  6,  8,  0, 13,  3,  4, 14,  7,  5, 11,
     10, 15,  4,  2,  7, 12,  9,  5,  6,  1, 13, 14,  0, 11,  3,  8,
     9, 14, 15,  5,  2,  8, 12,  3,  7,  0,  4, 10,  1, 13, 11,  6,
     4,  3,  2, 12,  9,  5, 15, 10, 11, 14,  1,  7,  6,  0,  8, 13],


[4, 11,  2, 14, 15,  0,  8, 13,  3, 12,  9,  7,  5, 10,  6,  1,
     13,  0, 11,  7,  4,  9,  1, 10, 14,  3,  5, 12,  2, 15,  8,  6,
     1,  4, 11, 13, 12,  3,  7, 14, 10, 15,  6,  8,  0,  5,  9,  2,
     6, 11, 13,  8,  1,  4, 10,  7,  9,  5,  0, 15, 14,  2,  3, 12],


[13,  2,  8,  4,  6, 15, 11,  1, 10,  9,  3, 14,  5,  0, 12,  7,
     1, 15, 13,  8, 10,  3,  7,  4, 12,  5,  6, 11,  0, 14,  9,  2,
     7, 11,  4,  1,  9, 12, 14,  2,  0,  6, 10, 13, 15,  3,  5,  8,
     2,  1, 14,  7,  4, 10,  8, 13, 15, 12,  9,  0,  3,  5,  6, 11],

]

#key

PC_1 = [57, 49, 41, 33, 25, 17,9,
       1, 58, 50, 42, 34, 26, 18,
      10,  2, 59, 51, 43, 35, 27,
      19, 11,  3, 60, 52, 44, 36,
      63, 55, 47, 39, 31, 23, 15,
       7, 62, 54, 46, 38, 30, 22,
      14,  6, 61, 53, 45, 37, 29,
      21, 13,  5, 28, 20, 12, 4]



PC_2 = [14, 17, 11, 24,  1,  5,  3, 28,
      15,  6, 21, 10, 23, 19, 12,  4,
      26,  8, 16,  7, 27, 20, 13,  2,
      41, 52, 31, 37, 47, 55, 30, 40,
      51, 45, 33, 48, 44, 49, 39, 56,
      34, 53, 46, 42, 50, 36, 29, 32]


#秘钥左移的位数
SHIFT = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]

test_rsa.py

from random import randrange
RSA_DEFAULT_EXPONENT = 65537
RSA_DEFAULT_MODULUS_LEN = 2048


first_50_primes = [3, 5, 7, 11, 13, 17, 19, 23, 29, 31,
                   37, 41, 43, 47, 53, 59, 61, 67, 71, 73,
                   79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
                   131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
                   181, 191, 193, 197, 199, 211, 223, 227, 229, 233]


def generate_n_bit_odd(n: int):
    '''Generate a random odd number in the range [2**(n-1)+1, 2**n-1]'''
    assert n > 1
    return randrange(2 ** (n - 1) + 1, 2 ** n, 2)
# The first 50 prime numbers after 2


def get_lowlevel_prime(n):
    """Generate a prime candidate not divisible by first primes"""
    while True:
        # Obtain a random odd number
        c = generate_n_bit_odd(n)

        # Test divisibility by pre-generated primes
        for divisor in first_50_primes:
            if c % divisor == 0 and divisor ** 2 <= c:
                break
        else:
            # The for loop did not encounter a break statement,
            # so it passes low level primality test.
            return c


def miller_rabin_primality_check(n, k=20):
    '''Miller-Rabin Primality Test wwith specified round of test
    Input:
        n - n > 3, an odd integer to be tested for primality
        k - the number of rounds of testing to perfor
    Output:
        True  - passed (n is a strong probable prime)
        False - failed (n is a composite)'''

    # For a given odd integer n > 3, write n as (2^s)*d+1,
    # where s and d are positive integers and d is odd.
    assert n > 3
    if n % 2 == 0:
        return False

    s, d = 0, n - 1
    while d % 2 == 0:
        d >>= 1
        s += 1

    for _ in range(k):
        a = randrange(2, n - 1)
        x = pow(a, d, n)

        if x == 1 or x == n - 1:
            continue

        for _ in range(s):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            # The for loop did not encounter a break statement,
            # so it fails the test, it must be a composite
            return False

    # Passed the test, it is a strong probable prime
    return True


def get_random_prime(num_bits):
    while True:
        pp = get_lowlevel_prime(num_bits)
        if miller_rabin_primality_check(pp):
            return pp


def gcd(a, b):
    '''Computes the Great Common Divisor using the Euclid's algorithm'''
    while b:
        a, b = b, a % b
    return a


def lcm(a, b):
    """Computes the Lowest Common Multiple using the GCD method."""
    return a // gcd(a, b) * b

def exgcd(a, b):
    """Extended Euclidean Algorithm that can give back all gcd, s, t
    such that they can make Bézout's identity: gcd(a,b) = a*s + b*t
    Return: (gcd, s, t) as tuple"""
    old_s, s = 1, 0
    old_t, t = 0, 1
    while b:
        q = a // b
        s, old_s = old_s - q * s, s
        t, old_t = old_t - q * t, t
        a, b = b, a % b
    return a, old_s, old_t

def invmod(e, m):
    """Find out the modular multiplicative inverse x of the input integer
    e with respect to the modulus m. Return the minimum positive x"""
    g, x, y = exgcd(e, m)
    assert g == 1

    # Now we have e*x + m*y = g = 1, so e*x ≡ 1 (mod m).
    # The modular multiplicative inverse of e is x.
    if x < 0:
        x += m
    return x


def uint_from_bytes(xbytes: bytes) -> int:
    """This works only for unsigned (non-negative) integers."""
    return int.from_bytes(xbytes, 'big')


def uint_to_bytes(x: int) -> bytes:
    """This works only for unsigned (non-negative) integers.
    It does not work for 0."""
    if x == 0:
        return bytes(1)
    return x.to_bytes((x.bit_length() + 7) // 8, 'big')


class RSA:
    """Implements the RSA public key encryption/decryption with default
    exponent 65537 and default key size 2048"""

    def __init__(self, key_length=RSA_DEFAULT_MODULUS_LEN,
                 exponent=RSA_DEFAULT_EXPONENT, fast_decrypt=False):
        global privite_key
        self.e = exponent
        self.fast = fast_decrypt
        t = 0
        p = q = 2

        while gcd(self.e, t) != 1:
            p = get_random_prime(key_length // 2)
            q = get_random_prime(key_length // 2)
            t = lcm(p - 1, q - 1)

        self.n = p * q
        self.d = invmod(self.e, t)
        privite_key = self.d
        if (fast_decrypt):
            self.p, self.q = p, q
            self.d_P = self.d % (p - 1)
            self.d_Q = self.d % (q - 1)
            self.q_Inv = invmod(q, p)

    # 加密函数 self.e self.n为公钥
    def encrypt(self, binary_data: bytes):
        int_data = uint_from_bytes(binary_data)
        global public_key,N
        public_key=self.e
        N=self.n
        return pow(int_data, self.e, self.n)


    # 解密函数 self.d self.n为私钥
    def decrypt(self, encrypted_int_data: int):
        int_data = pow(encrypted_int_data, self.d, self.n)
        return self.e


    def generate_signature(self, encoded_msg_digest: bytes):
        """Use RSA private key to generate Digital Signature for given
        encoded message digest"""
        int_data = uint_from_bytes(encoded_msg_digest)
        return pow(int_data, self.d, self.n)

    def generate_signature_fast(self, encoded_msg_digest: bytes):
        # Use Chinese Remaider Theorem + Fermat's Little Theorem to
        # do fast RSA signature generation
        assert self.fast == True
        int_data = uint_from_bytes(encoded_msg_digest)
        s1 = pow(int_data, self.d_P, self.p)
        s2 = pow(int_data, self.d_Q, self.q)
        t = s1 - s2
        if t < 0:
            t += self.p
        h = (self.q_Inv * t) % self.p
        s = (s2 + h * self.q) % self.n
        return s

    def decrypt_fast(self, encrypted_int_data: int):
        # Use Chinese Remaider Theorem + Fermat's Little Theorem to
        # do fast RSA description
        assert self.fast == True
        m1 = pow(encrypted_int_data, self.d_P, self.p)
        m2 = pow(encrypted_int_data, self.d_Q, self.q)
        t = m1 - m2
        if t < 0:
            t += self.p
        h = (self.q_Inv * t) % self.p
        m = (m2 + h * self.q) % self.n
        return uint_to_bytes(m)

    def verify_signature(self, digital_signature: int):
        """Use RSA public key to decrypt given Digital Signature"""
        int_data = pow(digital_signature, self.e, self.n)
        return uint_to_bytes(int_data)


# ---- Test RSA class ----
alice = RSA(512, 3, True)
msg = b'Textbook RSA in Python'
ctxt = alice.encrypt(msg)

P1.py

import threading
import socket
import time
from test_rsa import *
from pyDes import des, PAD_PKCS5, ECB

##在RSA中，P1需要公钥，需要RSA的加密函数
##在DES中，需要使用RSA对DES的秘钥进行加密然后再传过去，然后用DES加密算法对发送的消息进行加解密

address = ('127.0.0.1', 5005)  # 服务端地址和端口
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
s.bind(address)  # 绑定服务端地址和端口
s.listen(5)
print('服务器已启动，等待客户端连接...')
conn, addr = s.accept()  # 返回客户端地址和一个新的 socket 连接 服务在这里处于阻塞状态
print('[+] Connected with', addr)
print('开始初始化...')

def send():
    time.sleep(5)
    print("请输入你的秘钥：")
    key = input().replace(' ', '')
    global GLO_KEY
    GLO_KEY=key
    key1=pow(int(key), int(public_key), int(N))
    print("加密后的RSA",key1)
    key1=str(key1)
    #print('对秘钥进行加密',key1)
    conn.sendall(key1.encode())
    #conn.sendall(key.encode())
    print("初始化结束，可以开始聊天 have fun!!!")
    while True:
        send = input('').encode()
        if send=='我们结束吧'.encode():
            break
            conn.close()
        des_obj = des(key, ECB, key, padmode=PAD_PKCS5)
        secret_bytes = des_obj.encrypt(send)
        #print("密文",secret_bytes)
        #对数据进行加密
        conn.sendall(secret_bytes)
    conn.close()
    s.close()

def my():
    global public_key,N
    public_key=conn.recv(1024)
    public_key=public_key.decode()
    print("收到对方的public_key",public_key)
    N=conn.recv(1024)
    N=N.decode()
    print("收到对方的N",N)
    while True:
        data = conn.recv(1024)
        # 对数据进行解密
        des_obj = des(str(GLO_KEY), ECB, str(GLO_KEY), padmode=PAD_PKCS5)
        data = des_obj.decrypt(data)
        print('', data.decode())


if __name__ == '__main__':
    #服务器部分
    p = threading.Thread(target=my)
    p.start()
    send()

P2.py

import threading
import socket
import time
import sys
from test_rsa import *
from pyDes import des, PAD_PKCS5, ECB

##在RSA中，P2需要私钥，需要RSA的解密函数
##在DES中，需要DES的加密解密函数

address = ('127.0.0.1', 5005)  # 服务端地址和端口
s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
print("客户端已启动")
try:
    s.connect(address)  # 尝试连接服务端
except Exception:
    print('[!] Server not found ot not open')
    sys.exit()


def send():
    msg_key=str(public_key)
    msg_n=str(N)
    s.sendall(msg_key.encode())
    time.sleep(2)
    s.sendall(msg_n.encode())
    while True:
        send = input('').encode()
        if send == '我们结束吧'.encode():  # 自定义结束字符串
            break
        des_obj = des(str(GLO_KEY), ECB, str(GLO_KEY), padmode=PAD_PKCS5)
        secret_bytes = des_obj.encrypt(send)
        s.sendall(secret_bytes)
    s.close()

def my():
    print("正在等待服务器发送秘钥...")
    global DES_KEY
    DES_KEY = s.recv(1024)
    DES_KEY = DES_KEY.decode()
    DES_KEY = pow(int(DES_KEY),int(privite_key),int(N))
    #print('收到的秘钥：', DES_KEY)
    global GLO_KEY
    GLO_KEY=DES_KEY
    print("已收到发来的秘钥，可以开始聊天 have fun!!!")
    while True:
        data = s.recv(1024)
        #对数据进行解密
        des_obj = des(str(DES_KEY), ECB, str(DES_KEY), padmode=PAD_PKCS5)
        data = des_obj.decrypt(data)
        print('', data.decode())


if __name__ == '__main__':
    p = threading.Thread(target=my)
    p.start()
    send()

三、运行结果

P1为服务器，也就是图中发方，P2为客户端，相当于图中收方，但是他们之间是能够进行全双工通信的，不是一个只能收，一个只能发。

1.首先启动服务器，等待客户端连接

2.启动客户端

3.这时的服务器受到了客户端发来的公钥 和 大整数N

4.服务器将用这些对自己的DES秘钥进行加密
这里需要注意的是DES秘钥长度固定为64bit，也就是8个字符，在输入时需要注意。

按回车，就可以通信啦

测试汉字：

测试字符串：

P1:

p2:

总结

一开始想直接用Python中的DES包和RSA包直接对数据进行加密，奈何格式不是很匹配，变换格式有些许麻烦，索性直接创建了两个Python文件来进行DES和RSA加密。