剑指offer之面试题36：数组中的逆序对-归并排序的应用

最新推荐文章于 2023-04-02 11:34:41 发布

原创最新推荐文章于 2023-04-02 11:34:41 发布 · 1.1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#归并排序 #面试题

算法专栏收录该内容

5 篇文章

订阅专栏

本文探讨了逆序对计数问题，并通过归并排序算法来求解。通过对剑指Offer上的代码进行分析，解释了如何利用归并排序稳定性的特点有效地计算出逆序对数量。

本题按着剑指offer上的代码敲了一下，感觉答案有点问题，我的疑问就是为什么data数组没有被修改，既然是归并，在上一步合并以后应该是排好序的，但是剑指offer上并没有看到修改data，所以有些疑惑，做了如下修改。还希望如果有人注意到我的问题的同学给予指正。

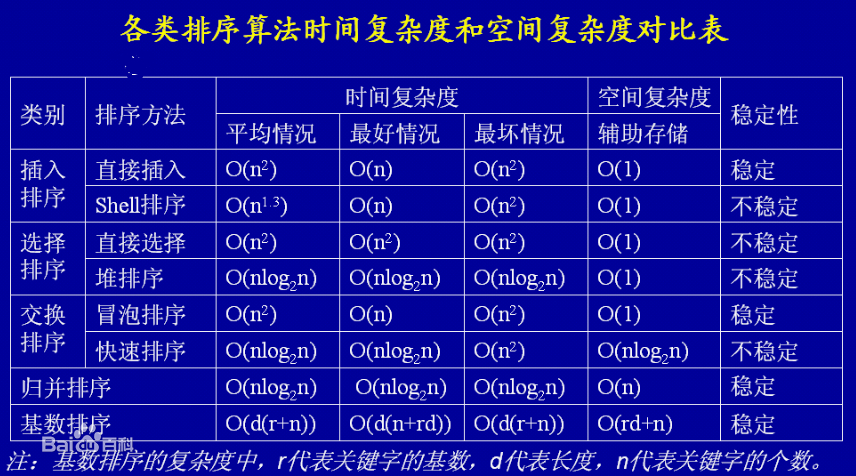
本题是一种排序算法的变形，我们只需记录排序算法中交换次数就可以知道逆序数的对数，而我们最先想到的两次for循环也是一种极为普通的排序的思路。更有效的是归并、堆排序、快速排序三种。但是在这三种排序中只有归并排序是稳定的，因此可以有效的反应出逆序对。因此我们选择归并排序的思路解决次问题。

int InversePairsCore(int* Data,int* Copy,int Start,int End){
    if(Start == End){
        Copy[Start] = Data[Start];
        return 0;
    }

    int length = (End-Start)/2;
    /****************左右两边的逆序数****************/
    int left = InversePairsCore(Data,Copy,Start,Start+length);
    int right = InversePairsCore(Data,Copy,Start+length+1,End);

    int i = Start + length;
    int j = End;
    int indexCopy = End;
    int Count = 0;
    /***************归并排序：并，类似排好序的两个链表排序*******************/
    while(i >= Start && j >= Start+length+1){
        if(Data[i]>Data[j]){
            Copy[indexCopy--] = Data[i--];
            Count += j-Start-length;//计倒序数
        }
        else
            Copy[indexCopy--] = Data[j--];
    }

    for(;i >= Start;--i)
        Copy[indexCopy--] = Data[i];

    for(;j >= Start+length+1;--j)
        Copy[indexCopy--] = Data[j];

    for(int k = 0;k <= End;k++)
        Data[k] = Copy[k];
    return left+right+Count;
}

int InversePair(int* str,int len){
    if(str == NULL || len < 0)
        return 0;
    int* Copy = new int[len];
    for(int i = 0;i < len;i++)//个人认为这个for循环没有必要，
        Copy[i] = str[i];
    int Count = InversePairsCore(str,Copy,0,len-1);
    delete[] Copy;
    return Count;
}