2021年12月7日 两数相加&&数组交集

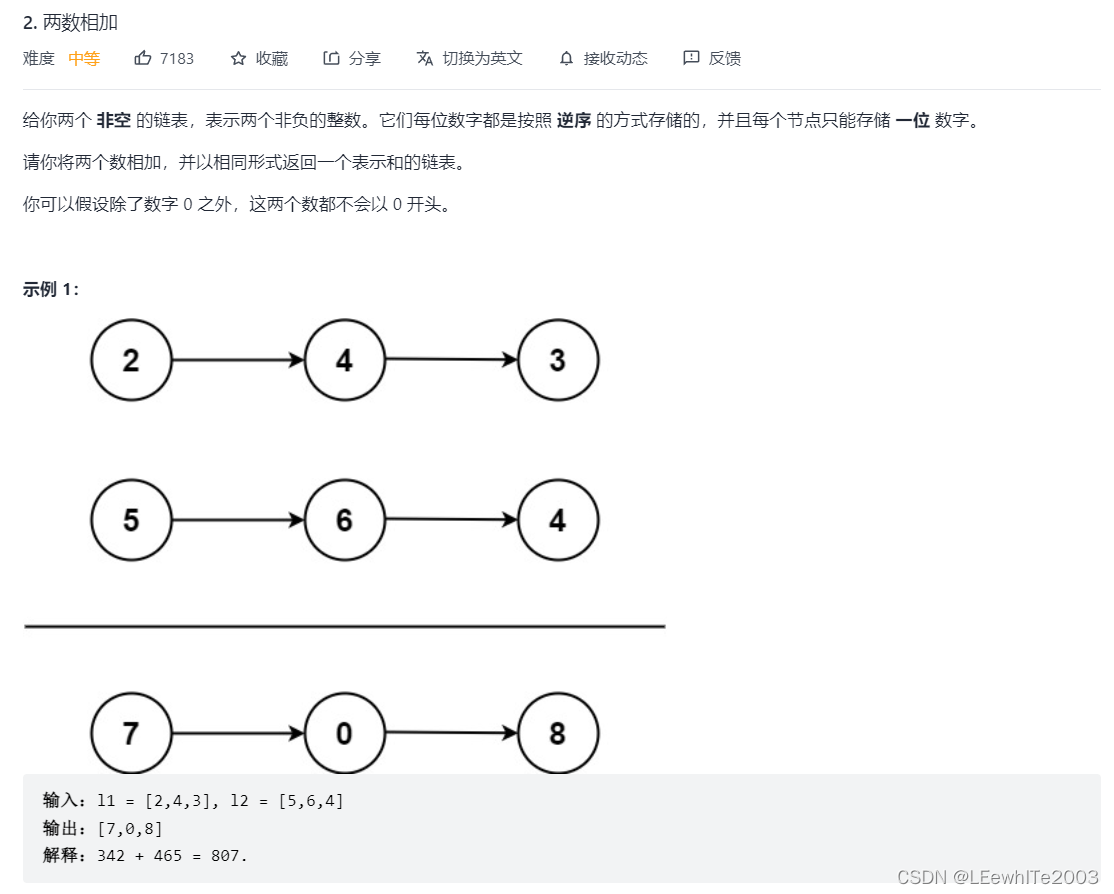
 思路：每位相加，大于十进位。

class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        if(!l1||!l2) return NULL;
        ListNode*head=new ListNode; "虚拟头结点"
        ListNode*p1=l1,*p2=l2,*p3=head;
        int key,pre=0;
        while(p1&&p2){
            key=p1->val+p2->val+pre;
            if(key>=10){
                pre=1;       "进位"
                key=key-10;  "key截取值"
            }
            else
                pre=0;  "pre重新更新为0"
            p3->next=Create(key);
            p3=p3->next;
            p1=p1->next;
            p2=p2->next;
        }
        ListNode* p=p1?p1:p2; "对剩余节点的处理"
        while(p){
            key=p->val+pre;
            if(key>=10){
                pre=1;
                key=key-10;
            }
            else
                pre=0;
            p3->next=Create(key);
            p3=p3->next;
            p=p->next;
        }
        if(pre)
            p3->next=Create(1);
        return head->next;
    }
    ListNode* Create(int key){
        ListNode*p=new ListNode;
        p->val=key;
        p->next=NULL;
        return p;
    }
};

大佬的写法，很简洁。

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode p1 = l1, p2 = l2;
        ListNode dummy = new ListNode(-1);
        ListNode p = dummy;
        int carry = 0, newVal = 0;
        while (p1 != null || p2 != null || carry > 0) {
            "这个条件能一直走下去，不用像我一样去做尾处理"
            newVal = (p1 == null ? 0: p1.val) + (p2 == null ? 0: p2.val) + carry; 
            "这个判断就很灵性"
            carry = newVal / 10;
            "carry相当于我的pre"
            newVal %= 10;
            p.next = new ListNode(newVal);
            p1 = p1 == null? null: p1.next;
            p2 = p2 == null? null: p2.next;
            p = p.next;
        }
        return dummy.next;
    }
}

---

 

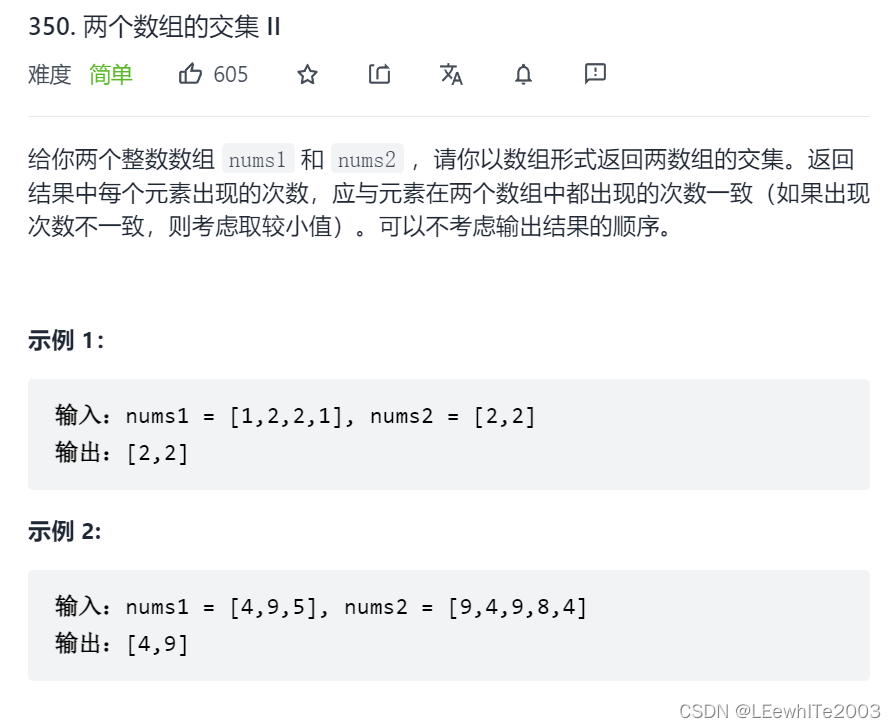
思路：

如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

首先对两个数组进行排序，然后使用两个指针遍历两个数组。

初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，将该数字添加到答案，并将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束。

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(),nums1.end());
        sort(nums2.begin(),nums2.end());
        int i=0,j=0;
        vector<int> nums3;
        while(i<nums1.size()&&j<nums2.size()){
            if(nums1[i]<nums2[j])
                i++;
            else if(nums1[i]>nums2[j])
                j++;
            else{
                nums3.push_back(nums1[i]);
                i++;
                j++;
            }
        }
        return nums3;
    }
};

时间复杂度：O(m \log m+n \log n)O(mlogm+nlogn)，其中 mm 和 nn 分别是两个数组的长度。对两个数组进行排序的时间复杂度是 O(m \log m+n \log n)O(mlogm+nlogn)，遍历两个数组的时间复杂度是 O(m+n)O(m+n)，因此总时间复杂度是 O(m \log m+n \log n)O(mlogm+nlogn)。

空间复杂度：O(\min(m,n))O(min(m,n))，其中 mm 和 nn 分别是两个数组的长度。为返回值创建一个数组 intersection，其长度为较短的数组的长度。不过在 C++ 中，我们可以直接创建一个 vector，不需要把答案临时存放在一个额外的数组中，所以这种实现的空间复杂度为 O(1)O(1)。

 

方法二：哈希表

由于同一个数字在两个数组中都可能出现多次，因此需要用哈希表存储每个数字出现的次数。对于一个数字，其在交集中出现的次数等于该数字在两个数组中出现次数的最小值。

首先遍历第一个数组，并在哈希表中记录第一个数组中的每个数字以及对应出现的次数，然后遍历第二个数组，对于第二个数组中的每个数字，如果在哈希表中存在这个数字，则将该数字添加到答案，并减少哈希表中该数字出现的次数。

为了降低空间复杂度，首先遍历较短的数组并在哈希表中记录每个数字以及对应出现的次数，然后遍历较长的数组得到交集。

（PS：如果元素存储在磁盘上，磁盘内存是有限的，并且你不能一次加载所有的元素到内存中。那么就无法高效地进行排序，因此推荐使用方法一而不是方法二。在方法一中，只关系到查询操作，因此每次读取中的一部分数据，并进行处理即可。）

class Solution {
public:
    vector<int> intersect(vector<int>& nums1, vector<int>& nums2) {
        if (nums1.size() > nums2.size()) {
            return intersect(nums2, nums1);
        }
        unordered_map <int, int> m;
        for (int num : nums1) {
            ++m[num];
        }
        vector<int> intersection;
        for (int num : nums2) {
            if (m.count(num)) {
                intersection.push_back(num);
                --m[num];
                if (m[num] == 0) {
                    m.erase(num);
                }
            }
        }
        return intersection;
    }
};

 时间复杂度：O(m \log m+n \log n)O(mlogm+nlogn)，其中 mm 和 nn 分别是两个数组的长度。对两个数组进行排序的时间复杂度是 O(m \log m+n \log n)O(mlogm+nlogn)，遍历两个数组的时间复杂度是 O(m+n)O(m+n)，因此总时间复杂度是 O(m \log m+n \log n)O(mlogm+nlogn)。

空间复杂度：O(\min(m,n))O(min(m,n))，其中 mm 和 nn 分别是两个数组的长度。为返回值创建一个数组 intersection，其长度为较短的数组的长度。不过在 C++ 中，我们可以直接创建一个 vector，不需要把答案临时存放在一个额外的数组中，所以这种实现的空间复杂度为 O(1)O(1)。