2021-10-27 链表，双指针

环形链表

         

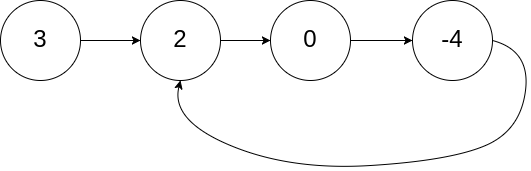
         如上图所示，链表出现了环的结构。

操作一：判断一个链表是否为环形链表

         最初思考：暴力就好了，每个节点附带一个flag域，初始化为0，如果第一次访问过就是1，一直p=p->next下去，如果找到某个节点的flag是1不是0，那么返回status==TRUE;

        不难看出来，如果链表是一个首尾相顾的环，这样子做空间复杂度是O(N)【因为多了很多个flag域】,而且此时最糟糕的时间复杂度是O(N)

        有没其他办法？

        有的！双指针！

        如果有环，类比于队列，一定会有"回溯"这个过程，那么假设两个指针一快一慢，那么快指针必定会先遍历完整个链表，之后进入"回溯"的过程，这样子，总会有快指针追上慢指针的时候。当快指针追上慢指针的时候，就说明这个链表不是单向的了，而是有一个闭环。

Status isCircle(List a){
    Polynode fast=a,slow=a;
    if(!a) return false;
    while(fast&&fast->next){
        "(测试条件其实也起到了排查探路的作用，一下子排查两个位点）"

        fast=fast->next->next;-----"快指针一下子走两格"
        "(不要怕fast->next是空指针报错，这就是为什么要在入口判断处加上"fast->next"的原因)"
        slow=slow->next;-----------"慢指针每次只前进一格"

        if(slow==fast)
        return true;"(如果有出现slow和fast重合的情况，我们就直接退出函数，返回个true)"
    }
    "(循环能出来肯定就是因为fast或者fast->next为空，因为重合的情况已经在上面处理过了）"
    return false;
    }

操作二：寻找环的入口 

环的入口位置的证明设计数论知识（🙄？？？）

其实画图就可以知道了，关键是设出“相遇点”这个关键的位置。

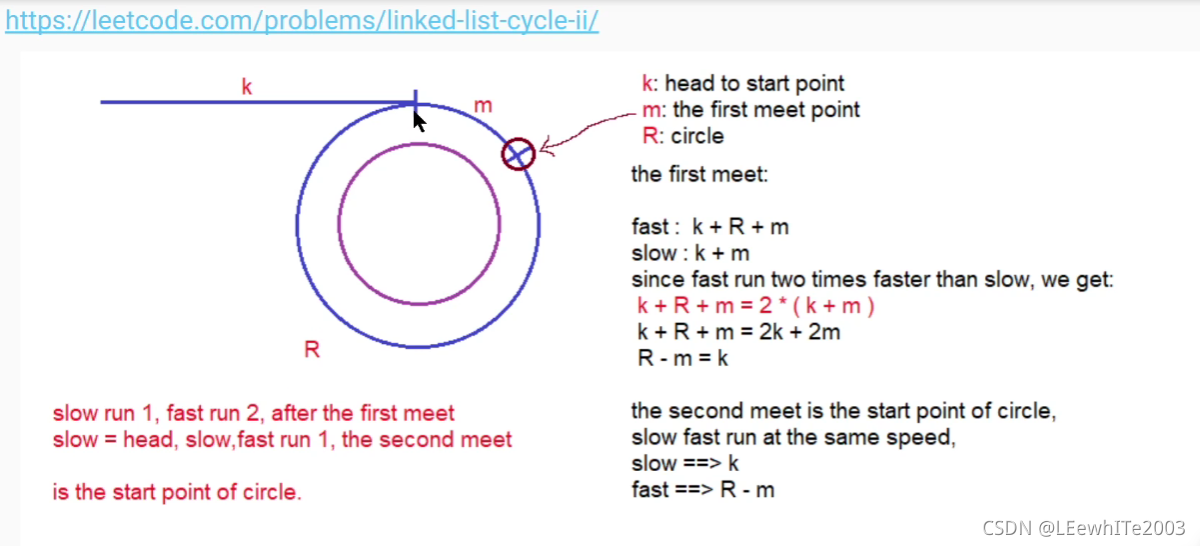
豁然开朗了！

原来 一旦快慢指针相遇，将慢指针移到链表起点，快指针停在他们相遇的地方，即离环的起点距离m的地方。然后慢指针和快指针同时移动，每次移动一步(快指针变慢），那么两者再次相遇的地方就是环的起点（根据R=m+k)。

Polynode circle_entrance(List L){
    Polynode fast=L,slow=L,temp"保存相遇位置";
    "在进行代码实现之前，先明确目标：完成1次循环->跳出循环->慢指针回溯，快指针降速，异地同时出发"
    while(fast&&fast->next){"这里和判断环函数一样"
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
            break；
    }
    if(!fast||!fast->next) return NULL;"链表不是环"
    else{
    slow=L; "slow的回溯"
    while(slow!=fast){"已经是环啦，不要再判断是不是空指针啥的啦"
    fast=fast->next;"fast减速"
    slow=slow->next;
    }
    return slow;
}
    
    
        
        
    
    

操作三：求环的长度 

有了入口怎么求环呢？

思路一：直接计数器暴力往下走？当然可以了。

思路二：这里注意到一个小特性，快指针走的路程总是慢指针的两倍，那么快指针走2圈，慢指针正好走1圈，而此时两个指针路程差正好是1圈，这就意味着两个指针相遇了。

"思路一"
int circle_length(List L){
    if(!iscircle(L)) return 0;
    Polynode entry=cirlce_entrance(L); "获取入口"
    Polynode p=entry; "游标指针，完成遍历"
    int i=1;
    while(p->next!=entry){
        i++;
        p=p->next;
    }
    return i;
}

"思路二"
int circle_length(List L){
    Polynode fast,slow;
    int i=1;
    if(!iscircle(L)) return 0;
    fast=slow=cirlce_entrance(L);
    do{
    fast=fast->next->next;
    slow=slow->next;
    i++;
    }while(fast!=slow);
    return i;
}
    

上述两个思路都利用了"circle_entrance"函数，下面是不利用circle_entrance函数的实现

大佬的原文链接：[算法]判断一个链表是否有环及环开始的位置_duxinyuhi的专栏-优快云博客_检测一个链表是否有环

//计算环的长度  
int loopLength(pNode pHead)  
{  
    if(isLoop(pHead) == false)  
        return 0;  
    pNode fast = pHead;  
    pNode slow = pHead;  
    int length = 0;  
    bool begin = false;  
    bool agian = false;  
    while( fast != NULL && fast->next != NULL)  
    {  
        fast = fast->next->next;  
        slow = slow->next;  
        //超两圈后停止计数，挑出循环  
        if(fast == slow && agian == true)  
            break;  
        //超一圈后开始计数  
        if(fast == slow && agian == false)  
        {             
            begin = true;  
            agian = true;  
        }  

        //计数  
        if(begin == true)  
            ++length;  

    }  
    return length;  
}

操作四：如果存在环，求出环上距离任意一个节点最远的点（对面节点）；

         首先明确一件事，那就是如果一个链表有环那么环必定在“链表的尾部”，因为一个节点只有一个指针域啊！！！所以不可能出现既指向后续线性节点又指向环节点的情况。

        接下来分析问题：

        1、将节点分成两类，一类在环上，一类不在环上；

        2、不在环上：

                在环上：

        

应用：判断两个链表是否有交叉

核心思想：将一个链表首尾相连变成环，用另外一个链表去判断是不是环！！！ 

Status iscommon(List L1,List L2){
    if(!L1||!L2) return NULL;
    Polynode p1=L1,p2=L2;
    Polynode fast=L2,slow=L2;
    "现在开始构建环"
    while(p1->next!=NUll)
        p1=p1->next;
    p1->next=L1;-----"首尾相连，自连成环；也可以连到另外一条链L2上"
    "开始以"非环链"（未遍历的那条链)判断是不是环链表"
    while(fast&&fast->next){
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast)
        return true;
    }
    return false;
}

 如果要找出公共节点呢？一样的！

Poly common_point(List L1,List L2){
    if(!L1||!L2) return NULL;
    Polynode p1=L1,p2=L2;   "选定L1作为"
    Polynode fast=L2,slow=L2;  "选定L2作为待检查环的链表"
    int flag=0;  "用作判断链表是不是环"

    "开始自建环，首尾相连"
    while(p1->next!=NUll)
        p1=p1->next;
    p1->next=L1;

    "开始对L2做环判断"
    while(fast&&fast->next){
        fast=fast->next->next;
        slow=slow->next;
        if(slow==fast){
        flag=1;
        break;
        }
    }
    if(!flag)
        return NULL;

    "判断结束，开始找入口（即公共点）"
    slow=L2;
    while(slow!=fast){
        slow=slow->next;
        fast=fast->next;
    }
    return slow;
}

---

 另外的解法，来自力扣：力扣

存在两种情况，A、B链表等长或者A、B不等长；

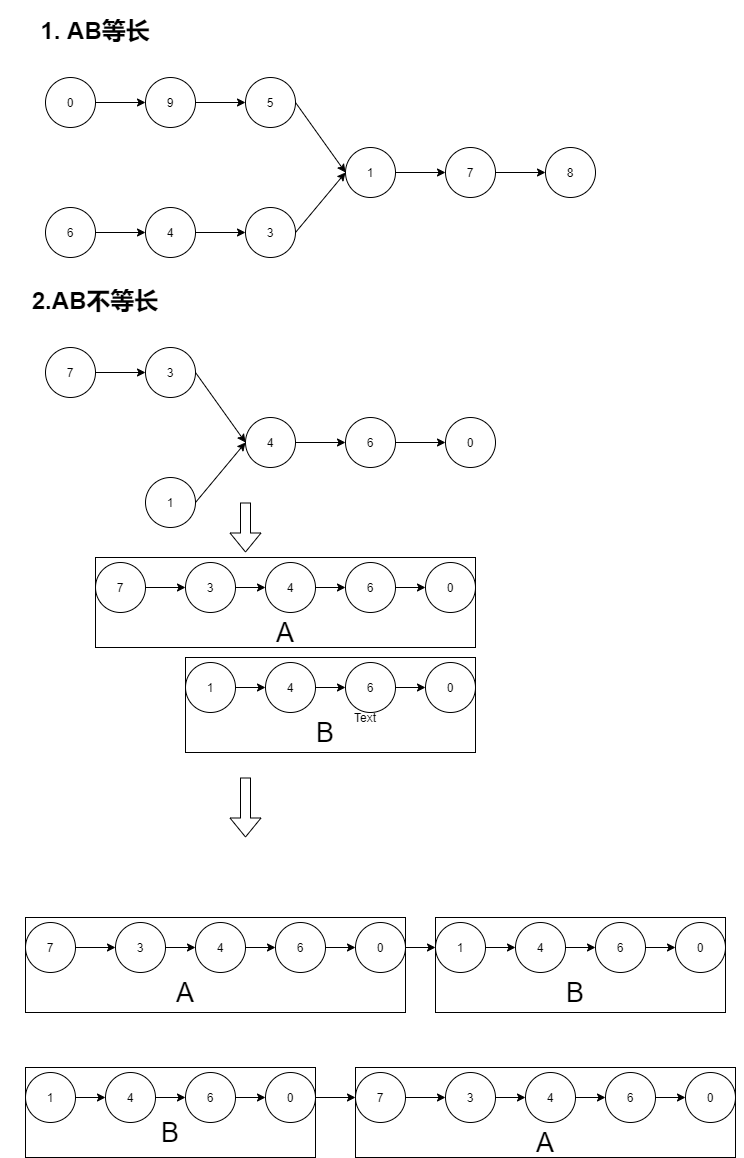
无论两链表是否相交，只需要将链表LA和链表LB的链尾对齐，然后从后向前依次比较节点是否相同即可。
   

 public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p1 = headA, p2 = headB;
        //变轨次数
        int cnt=0;
        while (p1 != null && p2 != null) {
            if (p1 == p2) return p1;
            p1 = p1.next;
            p2 = p2.next;
            //p1变轨
            if(cnt<2&&p1==null){
                p1=headB;
                cnt++;
            }
            //p2变轨
            if(cnt<2&&p2==null){
                p2=headA;
                cnt++;
            }
        }
        return null;
    }

时间复杂度:O(lA+lB)
空间复杂度:O(1)
不断的去对方的轨迹中寻找对方的身影，只要二人有交集，就终会相遇。

---