softmax交叉熵为什么要取"-log"
#######################################################################################
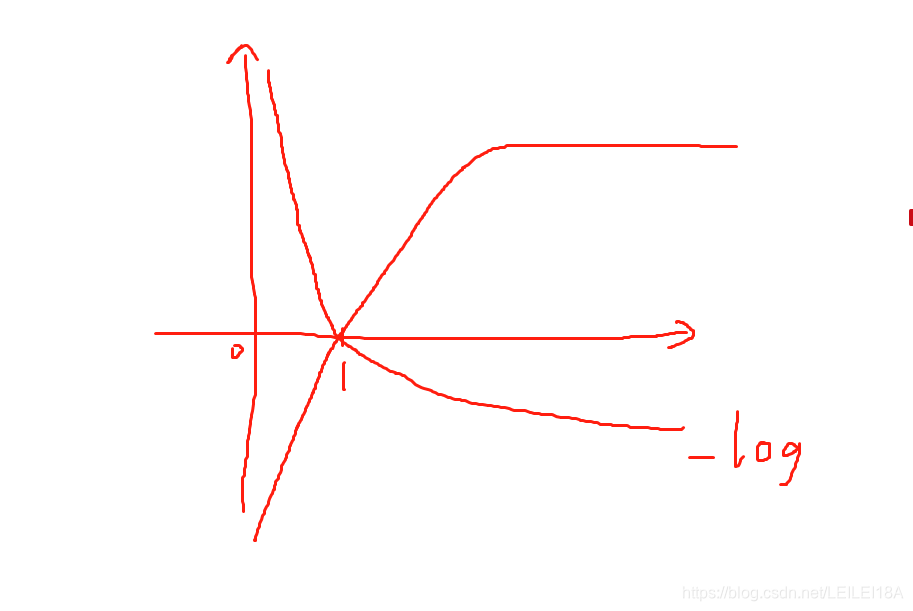
如图:-log是递减函数,对应着 错误越大包含信息越多,越正确包含信息越少,所以给错的比例越大。
而softmax之后,全部在【0,1】之间,越接近1,比例接近0;越接近0,比例无限大。从而可以学习正确的东西。
 本文深入探讨了Softmax函数和交叉熵损失函数在机器学习中的应用,解释了为何使用-log进行权重调整,以及如何通过这种方式使模型更有效地学习正确的分类。
本文深入探讨了Softmax函数和交叉熵损失函数在机器学习中的应用,解释了为何使用-log进行权重调整,以及如何通过这种方式使模型更有效地学习正确的分类。
softmax交叉熵为什么要取"-log"

#######################################################################################
如图:-log是递减函数,对应着 错误越大包含信息越多,越正确包含信息越少,所以给错的比例越大。
而softmax之后,全部在【0,1】之间,越接近1,比例接近0;越接近0,比例无限大。从而可以学习正确的东西。
您可能感兴趣的与本文相关的镜像

TensorFlow-v2.9
TensorFlow 是由Google Brain 团队开发的开源机器学习框架,广泛应用于深度学习研究和生产环境。 它提供了一个灵活的平台,用于构建和训练各种机器学习模型

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


