10141 棋盘分割

描述

将一个 8 × 8 的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了 (n−1) 次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。 (每次切割都只能沿着棋盘格子的边进行)

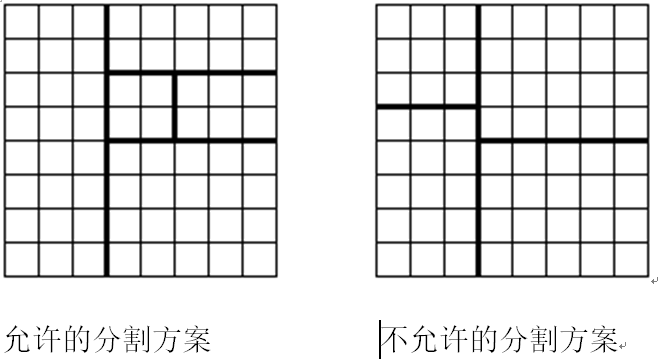
原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成 n 块矩形棋盘，并使各矩形棋盘总分的均方差最小。

均方差 σ=n∑i=1n​(xi​−xˉ)2​​ ，其中平均值 xˉ=n∑i=1n​xi​​ , xi​ 为第 i 块矩形棋盘的分。

请编程对给出的棋盘及 n ，求出 σ 的最小值。

输入描述

第一行为一个整数 n (1<n<15)。

第二行至第九行每行为 8 个小于 100 的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出描述

仅一个数，为 σ （四舍五入精确到小数点后三位）。

样例输入 1 

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

样例输出 1 

1.633

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
 
using std::sqrt;
using std::min;
 
const int WIDTH = 8;
const int MAXN = 15 + 1;
const int INF = 0x3f3f3f3f;
 
int a[WIDTH + 1][WIDTH + 1];
int nSum[WIDTH + 1][WIDTH + 1][WIDTH + 1][WIDTH + 1];
int nSquare[WIDTH + 1][WIDTH + 1][WIDTH + 1][WIDTH + 1];
int dp[WIDTH + 1][WIDTH + 1][WIDTH + 1][WIDTH + 1][MAXN];
 
void Init()
{
    memset(nSum, 0, sizeof(nSum));
    for (int x1 = 1; x1 <= WIDTH; ++x1)
    {
        for (int y1 = 1; y1 <= WIDTH; ++y1)
        {
            for (int x2 = x1; x2 <= WIDTH; ++x2)
            {
                for (int y2 = y1; y2 <= WIDTH; ++y2)
                {
                    nSum[x1][y1][x2][y2] = nSum[x1][y1][x2 - 1][y2] + nSum[x1][y1][x2][y2 - 1] - nSum[x1][y1][x2 - 1][y2 - 1] + a[x2][y2];
                    nSquare[x1][y1][x2][y2] = nSum[x1][y1][x2][y2] * nSum[x1][y1][x2][y2];
                    dp[x1][y1][x2][y2][0] = nSquare[x1][y1][x2][y2];
                }
            }
        }
    }
}
 
void Dp(int n)
{
    for (int i = 1; i <= n - 1; ++i)
    {
        for (int x1 = WIDTH; x1 >= 1; --x1)
        {
            for (int y1 = 1; y1 <= WIDTH; ++y1)
            {
                for (int x2 = x1; x2 <= WIDTH; ++x2)
                {
                    for (int y2 = y1; y2 <= WIDTH; ++y2)
                    {
                        dp[x1][y1][x2][y2][i] = INF;
                        for (int j = x1; j < x2; ++j)
                        {
                            dp[x1][y1][x2][y2][i] = min(dp[x1][y1][x2][y2][i], dp[x1][y1][j][y2][i - 1] + nSquare[j + 1][y1][x2][y2]);
                            dp[x1][y1][x2][y2][i] = min(dp[x1][y1][x2][y2][i], dp[j + 1][y1][x2][y2][i - 1] + nSquare[x1][y1][j][y2]);
                        }
                        for (int j = y1; j < y2; ++j)
                        {
                            dp[x1][y1][x2][y2][i] = min(dp[x1][y1][x2][y2][i], dp[x1][y1][x2][j][i - 1] + nSquare[x1][j + 1][x2][y2]);
                            dp[x1][y1][x2][y2][i] = min(dp[x1][y1][x2][y2][i], dp[x1][j + 1][x2][y2][i - 1] + nSquare[x1][y1][x2][j]);
                        }
                    }
                }
            }
        }
    }
}
 
void Output(int n)
{
    double fAvg = 1.0 * nSum[1][1][8][8] / n;
    printf("%.3f\n", sqrt(1.0 * dp[1][1][8][8][n - 1] / n - fAvg * fAvg));
}
 
void Read()
{
    for (int i = 1; i <= WIDTH; ++i)
    {
        for (int j = 1; j <= WIDTH; ++j)
        {
            scanf("%d", &a[i][j]);
        }
    }
}
 
int main()
{
    int n;
 
    while (scanf("%d", &n) == 1)
    {
        Read();
        Init();
        Dp(n);
        Output(n);
    }
 
    return 0;
}