Leetcode Hot 100 102.二叉树的层次遍历

1.题目

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

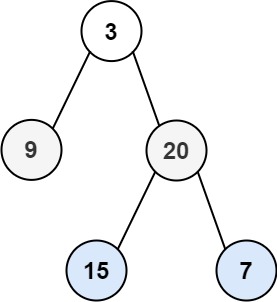
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

2.代码及解析

要使用队列了 

代码解析

1. 初始化:

   • 定义一个二维向量 ans，用于存储每一层的节点值。

   • 如果根节点 root 为空，直接返回空的 ans。

2. 使用队列进行 BFS:

   • 创建一个队列 que，并将根节点 root 入队。

   • 进入循环，直到队列为空：

     • 获取当前层的节点数量 size（即队列的当前大小）。

     • 定义一个一维向量 arr，用于存储当前层的节点值。

     • 遍历当前层的所有节点：

       • 从队列中取出队首节点 node。

       • 将 node 的值 node->val 加入 arr。

       • 如果 node 的左子节点不为空，将其入队。

       • 如果 node 的右子节点不为空，将其入队。

     • 将当前层的节点值 arr 加入 ans。

3. 返回结果:

   • 返回存储了所有层节点值的二维向量 ans。

代码逻辑

• 队列的作用:

  • 队列用于按层次存储节点，确保每一层的节点按从左到右的顺序被访问。

  • 每次处理完一层节点后，队列中会存储下一层的所有节点。

• 分层处理:

  • 通过 size 记录当前层的节点数量，确保每一层的节点值被正确地存储在一个单独的向量中。

• 时间复杂度:

  • 每个节点被访问一次，时间复杂度为 O(n)，其中 n 是树中节点的数量。

• 空间复杂度:

  • 队列的最大空间取决于树的最宽层，最坏情况下为 O(n)。

示例

假设有以下二叉树：

复制

      3
     / \
    9  20
      /  \
     15   7

• 层序遍历的结果为：

  复制

  [
    [3],
    [9, 20],
    [15, 7]
  ]

代码执行过程

1. 初始化队列 que，将根节点 3 入队。

2. 处理第一层：

   • 队列大小为 1，取出节点 3，将其值加入 arr。

   • 将 3 的左子节点 9 和右子节点 20 入队。

   • 将 arr = [3] 加入 ans。

3. 处理第二层：

   • 队列大小为 2，取出节点 9 和 20，将其值加入 arr。

   • 将 20 的左子节点 15 和右子节点 7 入队。

   • 将 arr = [9, 20] 加入 ans。

4. 处理第三层：

   • 队列大小为 2，取出节点 15 和 7，将其值加入 arr。

   • 这两个节点没有子节点，无需入队。

   • 将 arr = [15, 7] 加入 ans。

5. 队列为空，结束循环，返回 ans。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
         vector<vector<int>> ans;
        if (root == nullptr) return ans;
        queue<TreeNode*> que;
        que.push(root);
        while (!que.empty()) {
            int size=que.size();
            vector<int> arr;
            while(size--){
                TreeNode *node=que.front();
                que.pop();
                arr.push_back(node->val);
                if(node->left) que.push(node->left);
                if(node->right) que.push(node->right);
            }
            ans.push_back(arr);
        }
        return ans;

    }
};