684冗余连接（并查集）

题目链接：684. 冗余连接 - 力扣（LeetCode）

树可以看成是一个连通且 无环 的 无向 图。

给定一个图，该图从一棵 n 个节点 (节点值 1～n) 的树中添加一条边后获得。添加的边的两个不同顶点编号在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

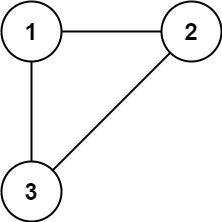
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

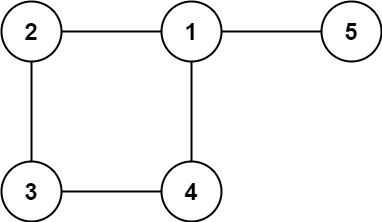
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:

• n == edges.length

• 3 <= n <= 1000

• edges[i].length == 2

• 1 <= ai < bi <= edges.length

• ai != bi

• edges 中无重复元素

• 给定的图是连通的

想要找到最后那条边，我们可以从前往后遍历edges，这个过程相当于将这些节点连接起来，以便于我们看到究竟是哪条边使图出现了环。

分析一下示例二：

1 -> 2 ✅

2 -> 3 ✅

3 -> 4 ✅

1 -> 4 ❌

所以我们要删除1 - 4这条边

抽象地说，之所以要删除1 - 4，是因为在将节点1和节点4连接起来之前，1和4就已经是可以相互到达的了，换言之，就是1和4已经在同一个集合中

这给予了我们启发：如果两个节点已经在同一个集合中，那么再将它们连接起来，就必然出现环

而并查集是判断两个节点是否在同一个集合中的常用套路，因此我们使用并查集处理此题：遍历edges，判断两个节点是否在同一集合中。如果是就找到答案，如果否就加入集合

class Solution 
{
public:
    int n=1005;//由提示可得n不超过1000
    vector<int>father=vector<int>(n,0);
    //并查集初始化
    void init() 
    {
        for(size_t i=0;i<father.size();i++)
        {
            father[i]=i;//每个人都没有领导与下属，自成一派
        }
    }
    //寻根
    int find(int u) 
    {
        return u==father[u]?u:father[u]=find(father[u]);
    }
    //判断两个节点是否在同一个集合中
    bool same(int u,int v)
    {
        return find(u)==find(v);
    }
    //加入集合
    void join(int u,int v)
    {
        if (find(u)==find(v)) return;//已经在同一个集合中
        u=find(u);
        v=find(v);
        father[v]=u;
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) 
    {
        init();
        for(auto& e:edges)
        {
            if(same(e[0],e[1]))
            {
                return {e[0],e[1]};
            }
            join(e[0],e[1]);
        }
        return {};
    }
};

并查集理解起来比较简单：可以理解成一堆人聚在一起玩一个游戏，找到自己的上司和自己的下属并手拉手连在一起

初始化：一开始大家都没有和别人拉手，相当于自己是自己的领导，自己是自己的下属

寻根：看看节点u是不是自己是自己的上司？如果是，那么它就是级别最高的领导，因为它没有上司了。如果不是，那么就往上找u的上一级领导father[u]，之所以让father[u]=find(father[u])，是为了精简整个人事体系。即在寻根的过程中，让u的上一级领导father[u]直接成为u的最高级别领导，这样u和最高级别领导就可以直接建立联系了，不需要经过一层又一层的领导

加入集合：如果u和v已经在同一个部门了，就没必要再拉手了。如果不是，那么u就成为了v的领导，拉手