题目链接:1584. 连接所有点的最小费用 - 力扣(LeetCode)
b站视频版讲解:
prim:https://t.bilibili.com/1067035550415847430?share_source=pc_native
kruscal:https://t.bilibili.com/1067025092172578820?share_source=pc_native
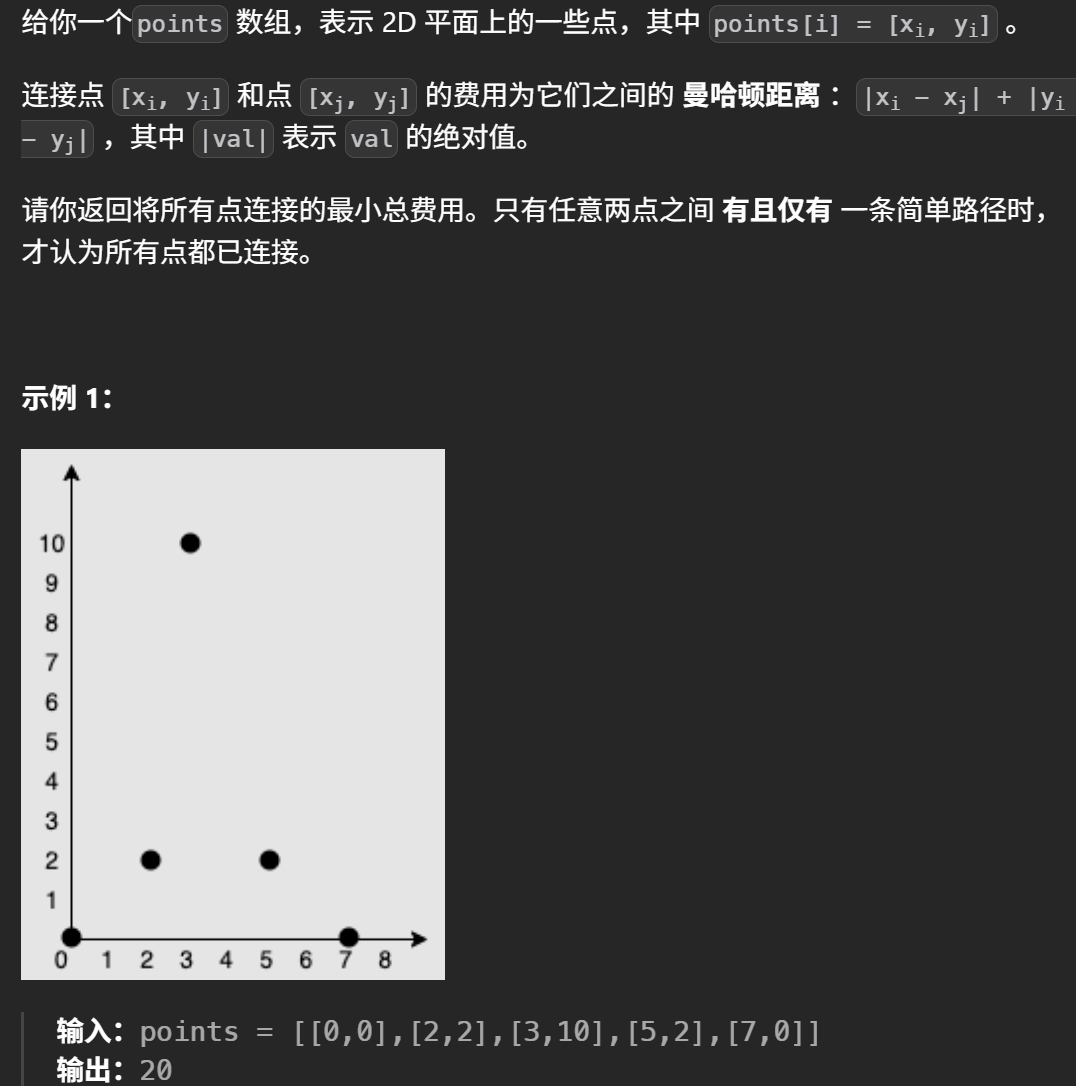
这是一道最小生成树的模板题。最小生成树问题一般指:在无向图中,希望用最小的成本将所有点都连接起来,其中成本指边权值。可以理解为修路,每个节点是一个城市,现在希望用最小的成本修路,以将这些城市都连接起来。
方法一:克鲁斯卡尔
其思路是维护边,这是比较好的,因为问题就是要让我们求最小边权值。然后根据边权值进行排序,贪心地从小到大选择,选择条件为:边两端的节点不在同一个集合当中。
如何判断两个节点是否在同一集合中?显然需要通过并查集。
class Solution
{
public:
void init(vector<int>&father,int n)//并查集初始化
{
father.resize(n);
for(int i=0;i<n;i++)
{
father[i]=i;
}
}
int find(vector<int>&father,int u)//寻根
{
return u==father[u]?u:father[u]=find(father,father[u]);
}
void join(vector<int>&father,int u,int v)//将两个节点加入到同一集合中
{
u=find(father,u);
v=find(father,v);
if(u==v)
{
return;
}
father[v]=u;
}
int dist(vector<vector<int>>&pts,int i,int j)//曼哈顿距离
{
return abs(pts[i][0]-pts[j][0])+abs(pts[i][1]-pts[j][1]);
}
struct Edge//维护边
{
int l,r,val;
Edge(int x,int y,int len):l(x),r(y),val(len){}
};
int minCostConnectPoints(vector<vector<int>>& points)
{
int n=points.size();
vector<int>father;
init(father,n);
vector<Edge>edge;
int ans=0;
int cnt=0;
for(int i=0;i<n;i++)
{
for(int j=i+1;j<n;j++)
{
edge.push_back({i,j,dist(points,i,j)});
}
}
sort(edge.begin(),edge.end(),[](const Edge&a,const Edge&b){return a.val<b.val;});
for(Edge e:edge)
{
int p1=e.l;
int p2=e.r;
if(find(father,p1)!=find(father,p2))//如果边的两个节点不在同一个集合中
{
join(father,p1,p2);
ans+=e.val;
cnt++;
}
if(cnt==n-1)//对于n个节点的图,只需要n-1条边就可以将它们连接起来
{
break;
}
}
return ans;
}
};方法二:普里姆
其思路是维护点。要定义一个数组min_dist,用来记录每个点到最小生成树的最小距离。
分三步:
1.选择到最小生成树距离最近的点
2.将该点加入到最小生成树当中
3.更新min_dist数组
class Solution
{
public:
//节点编号为1-n
int dist(vector<vector<int>>& pts, int i, int j)
{
return abs(pts[i-1][0] - pts[j-1][0]) + abs(pts[i-1][1] - pts[j-1][1]);
}
int minCostConnectPoints(vector<vector<int>>& points)
{
int n = points.size();
vector<vector<int>>graph(n+1, vector<int>(n+1));
int ans = 0;
for (int i = 1; i <= n; i++)//建图
{
for (int j = i + 1; j <= n; j++)
{
graph[i][j] = dist(points, i, j);
graph[j][i] = dist(points, j, i);
}
}
//1.找到 离最小生成树最近的节点->通过min_dist数组找
//2.将该节点加入最小生成树当中->bool
//3.更新min_dist数组
vector<bool>is_in(n + 1, false);
vector<int>min_dist(n + 1, INT_MAX);
min_dist[1] = 0;
for (int i = 1; i <= n; i++)//n次选择
{
//1.选择到最小生成树最近的节点cur
int cur = -1;//待选节点
int min_val = INT_MAX;
for (int j = 1; j <= n; j++)//遍历所有节点
{
if (!is_in[j] && min_dist[j] < min_val)
{
cur = j;
min_val = min_dist[j];
}
}
//2.将cur节点加入到最小生成树当中
is_in[cur] = true;
ans += min_dist[cur];
//3.更新min_dist
for (int j = 1; j <= n; j++)
{
//更新的条件:
//i:节点不在最小生成树当中
//ii:该节点到最小生成树的距离确实要更新->graph[cur][j]
if (!is_in[j] && min_dist[j] > graph[cur][j])
{
min_dist[j] = graph[cur][j];
}
}
}
return ans;
}
};什么叫确实要更新?就是说,该点j到最小生成树的最短距离会因为cur的加入而改变。原本cur没加入之前,j到最小生成树的最小距离为dis1,现在cur加入了,由于graph[cur][j]比dis1还要小,所以j到最小生成树的最小距离需要更新
 力扣1584:最小生成树算法解析
力扣1584:最小生成树算法解析




















 1049
1049

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








