激活函数sigmoid/tanh/relu区别

解释

训练网络做非线性变换时，经常会使用到 sigmoid/tanh/relu 激活函数，来增加网络的表达能力，公式为：

sigmoid: y = $\frac{1}{(1+e^{-x})}$
y 取值 (0, 1)

tanh: y = $\frac{(e^x-e^{-x})}{(e^x+e^{-x})}$
y 取值 (-1, 1)

relu: y = max(0, x)
y 取值 [0, +inf)

例子

import numpy as np
import matplotlib.pyplot as plt


def sigmoid(x):
    return 1 / (1 + np.exp(-x))


def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))


def relu(x):
    return np.maximum(0, x)


def main():
    x = np.arange(-5, 5, 0.1)
    p1 = plt.subplot(311)
    y = sigmoid(x)
    p1.plot(x, y)
    p1.set_title('sigmoid')
    p1.axhline(0.5, ls='--', color='r')
    p1.axvline(ls='--', color='r')

    p2 = plt.subplot(312)
    y = tanh(x)
    p2.plot(x, y)
    p2.set_title('tanh')
    p2.axhline(ls='--', color='r')
    p2.axvline(ls='--', color='r')

    p3 = plt.subplot(313)
    y = relu(x)
    p3.plot(x, y)
    p3.set_title('relu')
    p3.axvline(ls='--', color='r')

    plt.subplots_adjust(hspace=1)
    plt.show()
}


if __name__ == '__main__':
    main()

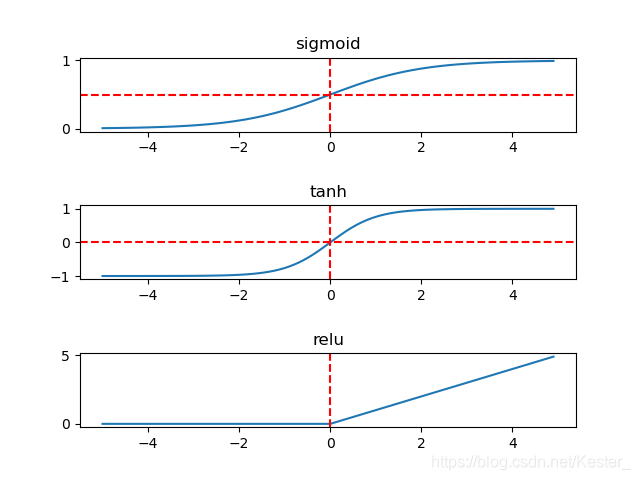
其中 sigmoid 和 tanh 是饱和激活函数，relu 是非饱和激活函数，更常用，可以有效预防梯度消失和梯度爆炸。