论文 Completely Self-Supervised Crowd Counting via Distribution Matching无监督算法详解

视频讲解：视频讲解（论文算法 + 代码详解）

论文下载地址：https://arxiv.org/pdf/2009.06420v1.pdf

代码下载地址：https://github.com/val-iisc/css-ccnn

论文Distribution Matching for Crowd Counting中人群统计损失（C Loss），最优化传输损失（OT Loss）以及总的变化损失（TV Loss）

论文CrowdCLIP（基于CLIP的无监督人群计数模型）详解（PyTorch,Pytorch_Lighting）

Opencv中的Canny边缘检测

        今天讲解的这篇论文属于无监督方面的算法点，其中的算法理解不是太容易，并且涉及的算法点也比较多，所以需要花较多的时间去理解和阅读。上一次我们讲过基于CLIP的无监督人群计数CrowdCLIP算法，那篇论文算法理解起来更加容易一点，并且代码实现方面理解起来也更加容易一点，因此也希望大家可以看一下那篇论文。

目录

一 目的和方法

提出目的

提出方法

二 人群分布规律

幂律分布（Power Law Distribution）

 累积分布函数

获得truncation的lambda 

过滤较小密度值

 生成truncation幂律分布

三 阶段1：自监督学习人群特征

四 阶段2：Sinkhorn训练

Sinkhorn算法详解​​

最优化传输问题

熵正则化

sinkhorn算法迭代流程

五 阶段2：进一步提升Sinkhorn训练

稀疏和稠密区域的划分流程

图像边缘检测和模糊实现

六 实验部分

综合实验效果对比 

 不同数据集效果对比

全监督和完全自监督

消融实验

不同先验选择

---

一 目的和方法

提出目的

        高密度人群计数是一项具有挑战性的任务，传统方法需要数百万个头像标注来训练模型。尽管现有自监督方法能够学习到良好的特征表示，但仍需部分标注数据将这些特征映射到密度估计的最终任务。

提出方法

        提出完全自监督的新范式，无需任何标注图像即可实现训练。除大量未标注人群图像外，该方法仅需输入数据集的近似人群数量上限作为先验信息。该方法基于自然人群服从幂律分布的特性，利用该统计规律生成反向传播误差信号。首先通过自监督预训练密度回归器，随后通过优化预测分布与先验分布的Sinkhorn距离实现特征对齐。

具体方法总结：针对标准自监督方法的核心局限——聚焦于人群密度估计任务，旨在彻底消除将自监督特征映射至密度图输出时对标注数据的强制依赖。换言之，致力于开发完全无需标注数据的训练范式。这一目标不仅极具挑战性，在数学上更属于不适定问题：缺乏监督信号时，模型既无法识别目标任务，也难以获得有效训练指引。

创新性地通过关键假设实现突破：

① 统计 先验约束​ ​
基于自然人群服从长尾分布的 特性， 将其建模为参数化 先验分布 ；

② 特征 - 密度映射机制​ ​
对自监督预训练 网络施加 分布匹配约束，通过 Sinkhorn 距离度量 预测与先验的差异并生成梯度 信号 ；

③ 框架 革新​ ​
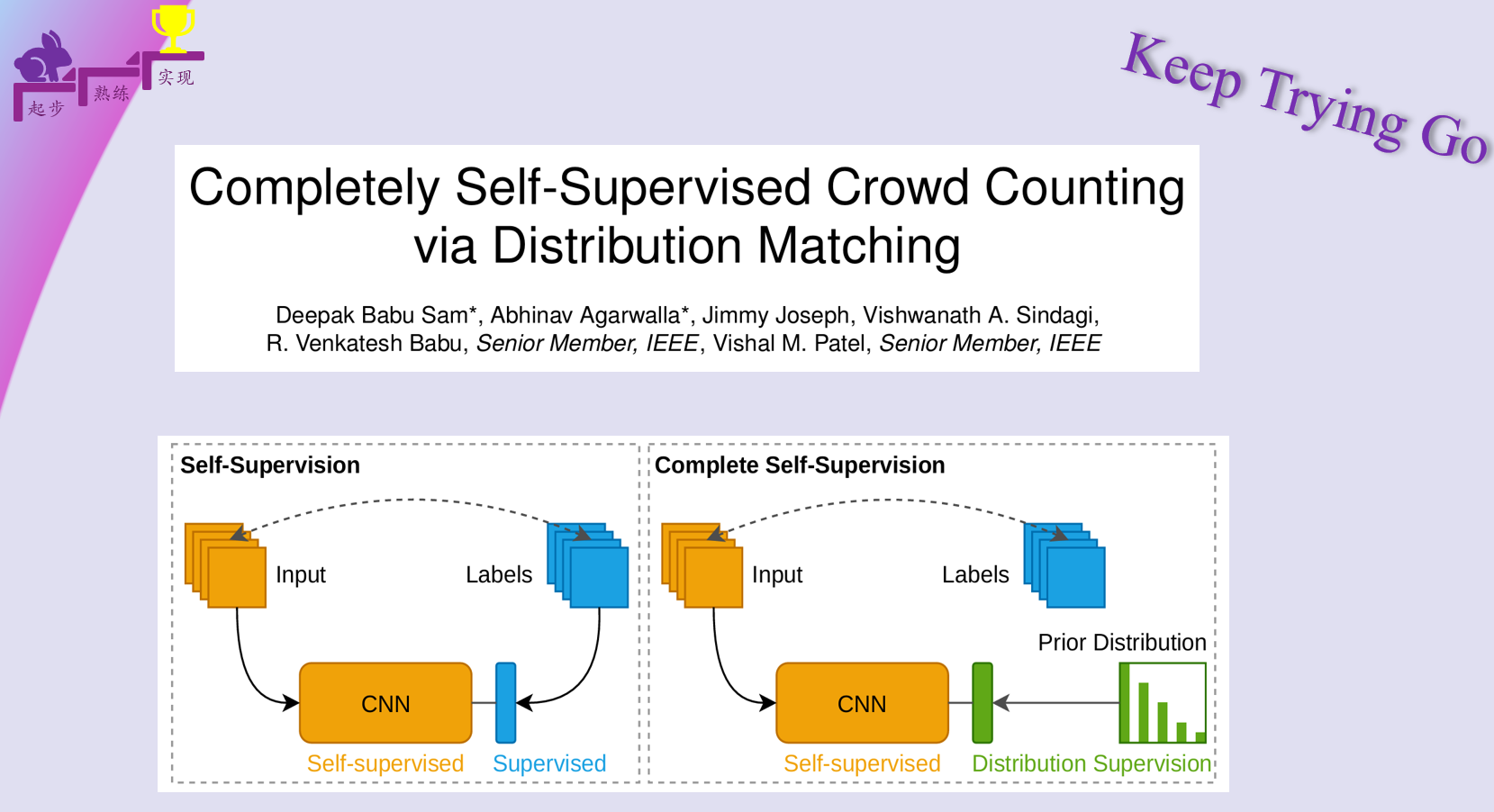
如图 1 所示，用分布匹配监督替代传统末端标注监督，实现完全无标注训练

二 人群分布规律

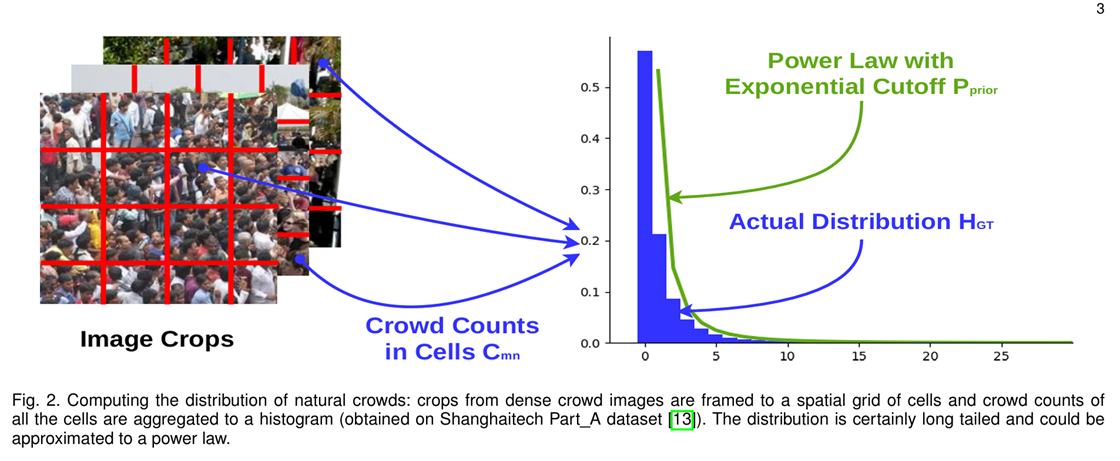
        密集人群计数任务中训练无需标注数据的密度回归器存在固有挑战，主要原因在于缺乏引导模型进行密度估计的监督信号。可通过挖掘任务特定结构模式加以解决。针对密集人群图像的分析发现，其密度分布呈现显著的长尾特性。

       通过固定尺寸图像块采样及网格划分（如图所示），统计各网格单元内人数分布直方图显示：
• 低密度区域形成分布头部（出现频率最高）
• 高密度区域构成分布尾部
• 人群密度与区域出现频率呈幂律衰减关系

        该分布模式与自然人群的空间排布规律一致——稀疏区域普遍存在，而极高密度区域相对罕见。值得注意的是，大量关于行人聚集动力学的研究证实，密集人群确实遵循此类幂律分布特征。这种统计规律为构建无监督训练信号提供了理论基础。

 Scrop描述图像被分成了多少个“子图”来预测，M×N是每个子图密度图的网格划分。

幂律分布（Power Law Distribution）

        是统计学中一种常见的重尾分布，其核心特征是​​事件发生的概率与其大小成反比关系​​，即小规模事件频繁发生，而大规模事件罕见但不可忽略。其数学表达式为：

 累积分布函数

def get_cdf(x, alpha, Lambda):
        CDF = ((gammainc(1-alpha, Lambda*x)) / Lambda**(1-alpha))
        return 1-CDF

注：我们这里给出的数学形式都是按照上面CDF的代码和gammainc表达式来写的。

获得truncation的lambda 

def get_lambda():
    m, n = 4, 4
    #TODO 将图像划分为[m,n]大小的网格，并且每一个网格的最大人数为max_value
    max_value = args.cmax / (args.scrop * m * n)
    #TODO 找到一个人群数小于最大值Cmax的概率
    for Lambda_t in np.arange(0.001, 0.1, 0.001):
        #TODO 计算累积概率密度，表示大于max_value的概率
        cdf = get_cdf(max_value, args.alpha, Lambda_t)
        #TODO 默认的num_samples大小为482
        if cdf > 1 - 1. / args.num_samples:
            return Lambda_t

过滤较小密度值

def get_shift_thresh():
    # TODO 找到一个人群数小于最大值Cmax的概率
    Lambda = get_lambda()
    for value in np.arange(1.01, 10, 0.01):
        #TODO 计算累积概率密度
        cdf = get_cdf(value, args.alpha, Lambda)
        if cdf > 0.28:
            return float("{0:.2f}".format(value))

• 遍历数值（1.01到10），计算每个值对应的 P(X>value)。
• 当概率首次超过28%时，返回该值作为阈值。
• ​​后续用于过滤过小的密度值（如将低于 shift_thresh 的值替换为均匀随机数）。

参数	数学意义	对分布的影响
alpha	幂律指数（α）	值越小，重尾特征越明显
Lambda	截断参数（Λ）	值越大，尾部衰减越快
x	随机变量取值	输入的计算点

 生成truncation幂律分布

            sampled_GT = None
            sampled_GT_shape = args.sbs * 7 * 7 * (8 // args.kernel_size) * (8 // args.kernel_size)
            #TODO 其中alpha控制形状，lambda用于控制尾部衰减速度
            sampling_parameters = [args.alpha, Lambda]
            #TODO 在给定参数的情况下，计算截断幂律分布：x^(−α) * e^(−λx)
            sampled_GT = powerlaw.Truncated_Power_Law(
                parameters=sampling_parameters
            ).generate_random(sampled_GT_shape)


            for s_i, s_val in enumerate(sampled_GT):
                #TODO 若样本值 < shift_thresh，则将其替换为[0, shift_thresh)区间内的均匀分布随机数。
                if s_val < shift_thresh:
                    sampled_GT[s_i] = np.random.uniform(low=0, high=shift_thresh)

三 阶段1：自监督学习人群特征

四 阶段2：Sinkhorn训练

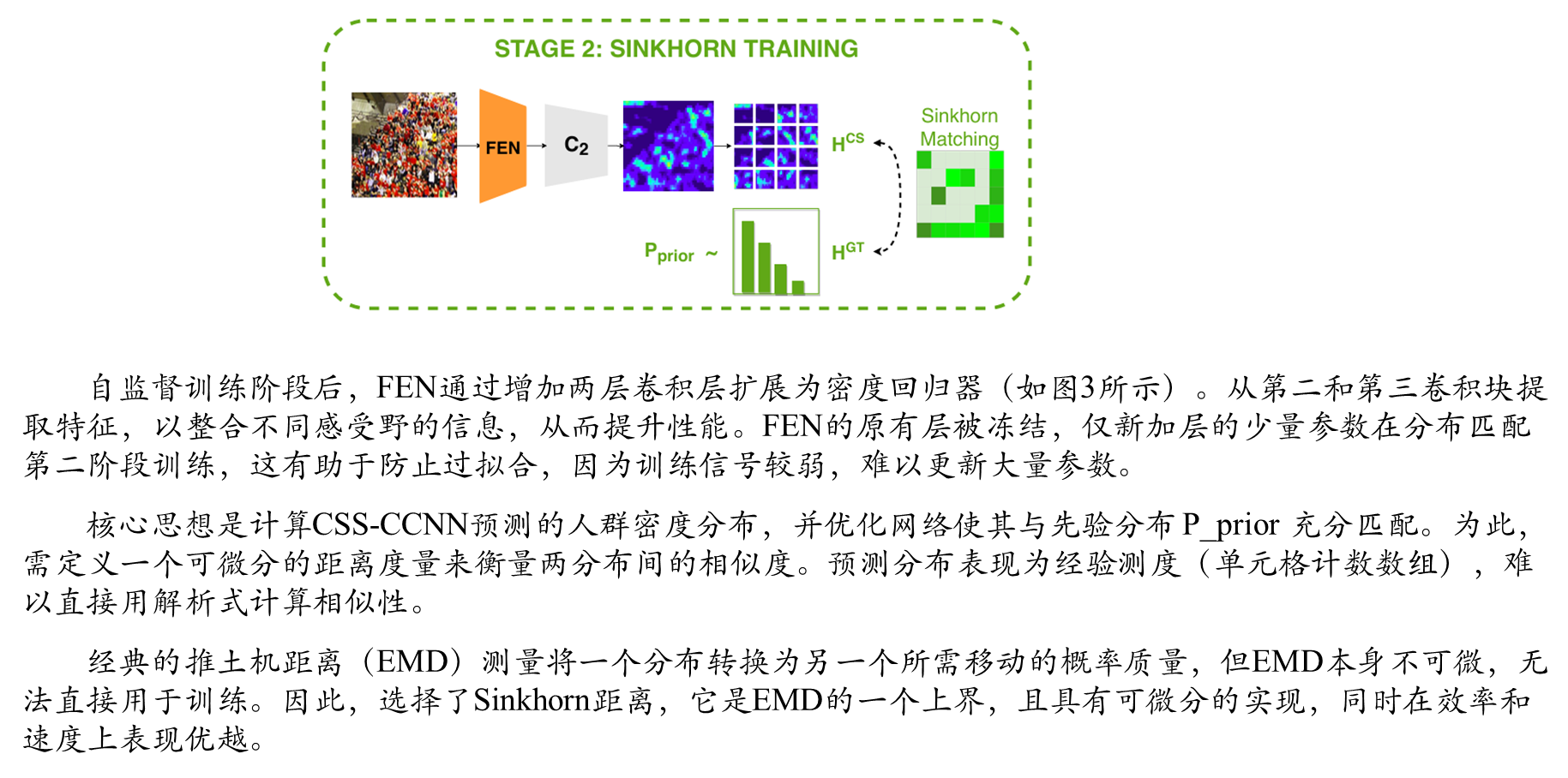
Sinkhorn算法详解​​

        Sinkhorn算法是一种基于​​最优传输（Optimal Transport, OT）​​的高效计算框架，用于求解两个概率分布之间的耦合矩阵（transport plan）。其核心思想是通过​​熵正则化（Entropic Regularization）​​将原本非光滑的线性规划问题转化为可微的凸优化问题，从而支持大规模高效计算。

论文Distribution Matching for Crowd Counting中人群统计损失（C Loss），最优化传输损失（OT Loss）以及总的变化损失（TV Loss）

最优化传输问题

其中耦合矩阵P是非负的，并且表示从源分布的第 i 个点向目标分布的第 j 个点传输的质量（或概率） ，直白的说是从源分布到目标分布的一种“运算方案”。代价矩阵C是非负的，并且表示​​从源分布的第 i 个点到目标分布的第 j 个点的传输成本，可以通过欧式距离或者其他公式来衡量源分布和目标分布之间的距离。

熵正则化

sinkhorn算法迭代流程

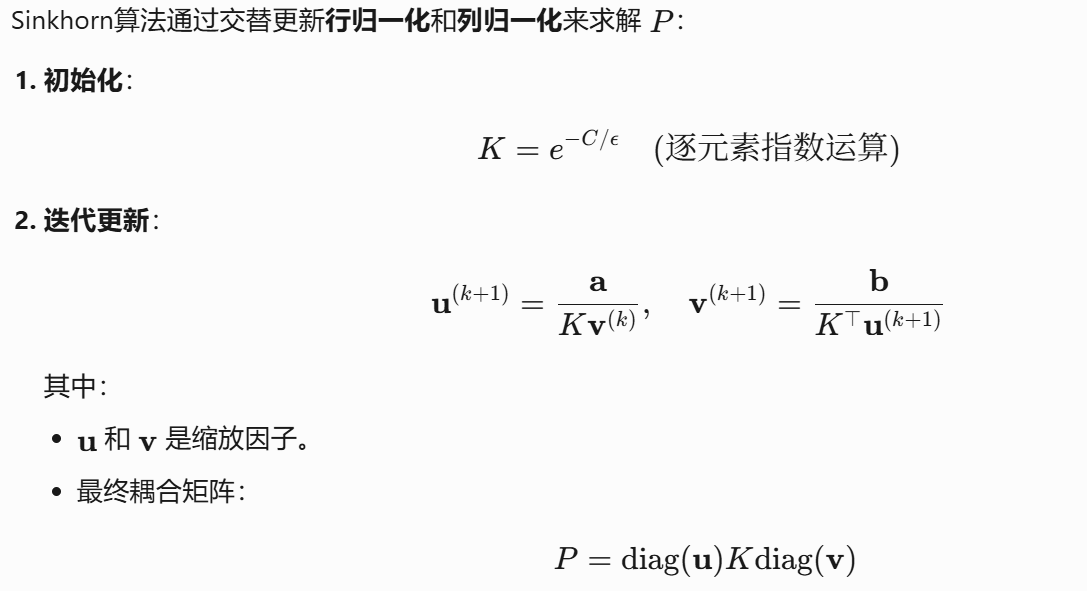
从下面的代码我们可以看到对于K的求解，代码中实际是通过：K = (u + v - C) / ε 来进行计算和，和给出的公式有所区别。

关于更多sinkhorn迭代算法的细节，请看：https://blog.youkuaiyun.com/weixin_44012667/article/details/146387606

import torch
import torch.nn as nn
from pdb import set_trace as bp

class SinkhornSolver(nn.Module):
    """
    Optimal Transport solver under entropic regularisation.
    Based on the code of Gabriel Peyré.
    """
    def __init__(self, epsilon, iterations=100, ground_metric=lambda x: torch.pow(x, 2)):
        super(SinkhornSolver, self).__init__()
        self.epsilon = epsilon
        self.iterations = iterations
        self.ground_metric = ground_metric

    def sinkhorn_loss(self, x, y):
        num_x = x.size(-2)
        num_y = y.size(-2)

        batch_size = 1 if x.dim() == 2 else x.size(0)

        # TODO 其中a和b分别表示源分布和目标分布 Marginal densities are empirical measures
        a = x.new_ones((batch_size, num_x), requires_grad=False) / num_x
        b = y.new_ones((batch_size, num_y), requires_grad=False) / num_y
        a = a.squeeze()
        b = b.squeeze()

        # TODO 缩放因子 Initialise approximation vectors in log domain
        u = torch.zeros_like(a)
        v = torch.zeros_like(b)

        # Stopping criterion
        threshold = 1e-1

        # TODO 计算代价矩阵 Cost matrix
        C = self._compute_cost(x, y)

        # TODO  Sinkhorn iterations
        # TODO 迭代过程中分别使用源分布和目标分布以及代价矩形对缩放因子u和v进行迭代更新
        # TODO 直到最后的缩放因子没有太大变化，表示得到一个合适的缩放因子，同时也得最终的耦合矩              阵（运算方案）
        for i in range(self.iterations):
            u0, v0 = u, v

            # TODO u^{l+1} = a / (K v^l)
            K = self._log_boltzmann_kernel(u, v, C)
            u_ = torch.log(a + 1e-8) - torch.logsumexp(K, dim=1)
            u = self.epsilon * u_ + u

            # TODO v^{l+1} = b / (K^T u^(l+1))
            K_t = self._log_boltzmann_kernel(u, v, C).transpose(-2, -1)
            v_ = torch.log(b + 1e-8) - torch.logsumexp(K_t, dim=1)
            v = self.epsilon * v_ + v

            # TODO 计算更新之前和更新之后的距离差异，也代表更新程度，如果更新程度不大就跳出循环 Size of the change we have performed on u
            diff = torch.sum(torch.abs(u - u0), dim=-1) + torch.sum(torch.abs(v - v0), dim=-1)
            mean_diff = torch.mean(diff)

            if mean_diff.item() < threshold:
                break

        # TODO Transport plan pi = diag(a)*K*diag(b)
        K = self._log_boltzmann_kernel(u, v, C)
        pi = torch.exp(K)

        # TODO Sinkhorn distance
        cost = torch.sum(pi * C, dim=(-2, -1))

        return cost

    def sinkhorn_normalized(self, x, y):
        Wxy = self.sinkhorn_loss(x, y)
        Wxx = self.sinkhorn_loss(x, x)
        Wyy = self.sinkhorn_loss(y, y)
        return 2 * Wxy - Wxx - Wyy

    def forward(self, x, y):
        # return self.sinkhorn_normalized(x,y)
        return self.sinkhorn_loss(x, y)

    def _compute_cost(self, x, y):
        x_ = x.unsqueeze(-2)
        y_ = y.unsqueeze(-3)
        #todo 计算代价就作为差的平方
        C = torch.sum(self.ground_metric(x_ - y_), dim=-1)
        return C

    def _log_boltzmann_kernel(self, u, v, C=None):
        C = self._compute_cost(u, v) if C is None else C
        kernel = -C + u.unsqueeze(-1) + v.unsqueeze(-2)
        kernel /= self.epsilon
        return kernel

五 阶段2：进一步提升Sinkhorn训练

稀疏和稠密区域的划分流程

这里我们再来捋一下思路：

• 第一步：对输入训练集的图像使用canny边缘检测算法获得检测结果；
• 第二步：经过canny检测之后使用高斯核对其进行模糊处理；
• 第三步：返回模糊处理之后的图像；
• 第四步：按照指定的阈值percentile_thresh 获得划分稀疏区域以及稠密区域的分界线；
• 第五步：根据分界线获得预测密度图的稀疏和稠密区域，对输入的标签（幂律分布）的处理也是要划分稀疏和稠密区域；
• 第六步：分别计算（预测密度图稀疏，标签稀疏）和（预测密度图稠密，标签稠密）的损失。

图像边缘检测和模糊实现

我们这里看一下上面第一步到第三步的处理可视化结果：

测试程序代码如下：

"""
@Author : Keep_Trying_Go
@Major  : Computer Science and Technology
@Hobby  : Computer Vision
@Time   : 2025/5/23-10:44
@优快云   : https://blog.youkuaiyun.com/Keep_Trying_Go?spm=1010.2135.3001.5421
"""

import cv2
import numpy as np
import torch


def create_pseudo_density(image):
    blur_sigma = 2
    # TODO 高斯核大小
    kernal_size_from_actual = 5
    # TODO 将图像转换为灰度图，并且使用canny提取边缘信息
    gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
    gray = cv2.Canny(gray, 225, 250)

    cv2.imwrite("./resources/canny.png",gray)

    # TODO 采用高斯对其灰度图进行模糊
    blur = cv2.GaussianBlur(
        gray,
        ksize=(kernal_size_from_actual, kernal_size_from_actual),
        sigmaX=blur_sigma
    )
    orig_blur = blur.copy()
    # TODO 归一化操作
    blur = blur.astype('float32') / 255
    blur = blur * 0.8 / 10

    blur_uint8 = np.clip(blur * (255 / 0.08), 0, 255).astype(np.uint8)
    cv2.imwrite("./resources/blur.png",blur_uint8)

    return blur

if __name__ == '__main__':
    image = cv2.imread(r"D:\conda3\Transfer_Learning\CrowdDataset\datasets\shanghai\ShanghaiTech\part_B\test_imgs\imgs\IMG_1.jpg")
    create_pseudo_density(image)

canny边缘检测算法：Opencv中的Canny边缘检测

核心代码：

def create_pseudo_density(Xs):
    global blur_sigma
    #TODO 高斯核大小
    kernal_size_from_actual = 5
    #TODO 保存返回的伪密度图
    pseudo_density_maps = []
    for i in range(Xs.shape[0]):
        #TODO 通道的转换和类型的转换为numpy
        image = Xs[i].transpose((1,2,0)).astype('uint8')#(224,224,3)

        #TODO 将图像转换为灰度图，并且使用canny提取边缘信息
        gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
        gray = cv2.Canny(gray, 225, 250)
        #TODO 缩放图像大小到指定的大小
        gray = cv2.resize(gray,(gray.shape[1]//output_downscale, gray.shape[0]//output_downscale))

        #TODO 采用高斯对其灰度图进行模糊
        blur = cv2.GaussianBlur(
            gray,
            ksize = (kernal_size_from_actual,kernal_size_from_actual),
            sigmaX = blur_sigma
        )

        orig_blur = blur.copy()
        #TODO 归一化操作
        blur = blur.astype('float32') / 255
        blur = blur * 0.8 / 10
        
        pseudo_density_maps.append(blur[None,...])
    
    pseudo_density_maps = np.array(pseudo_density_maps)
    pseudo_density_maps = pseudo_density_maps / np.max(pseudo_density_maps)
    return pseudo_density_maps

#TODO 这里对其原图进行灰度，边缘提取以及高斯模糊操作来得到图像的伪标签
    pseudo_density_maps = create_pseudo_density(Xs)
    pseudo_density_maps = torch.from_numpy(pseudo_density_maps).cuda()
    
    avg_pool = nn.AvgPool2d(kernel_size=args.kernel_size,
                            stride=args.kernel_size)
    #TODO 对预测的密度图和伪标签图进行下采样操作
    output_reshape_ = avg_pool(outputs) * (args.kernel_size * args.kernel_size)
    pseudo_reshape_ = avg_pool(pseudo_density_maps) * (args.kernel_size * args.kernel_size)
    output_reshape = output_reshape_.view(-1, 1)
    pseudo_reshape = pseudo_reshape_.view(-1, 1)

    # -- Split predictions into sparse, dense using percentile_thresh
    #TODO 根据指定的百分位阈值将其划分到稀疏和密集预测,默认percentile_thresh = 0.3,
    # 注意这里的len(pseudo_reshape)表示获得第一个维度大小
    """
        [0]：获取 topk 返回的 值张量（忽略索引张量）。
        [-1:]：取排序后的第 k 个值（即阈值边界）。
        [0]：去除多余的维度（从 [1, 1] 变为标量）。
    """
    pseudo_median = pseudo_reshape.topk(
        int(args.percentile_thresh*len(pseudo_reshape)), dim=0
    )[0][-1:][0]
    #TODO 对原图对应的标签（幂律分布）按百分位进行稀疏和密集的划分
    Y_median = Y.topk(int(args.percentile_thresh*(len(Y))), dim=0)[0][-1:][0]

    #TODO 稀疏和稠密区域的明确划分
    a_output_indices = pseudo_reshape < pseudo_median
    a_Y_indices = Y < Y_median

    if a_output_indices.sum() > 2:
        #TODO 计算稀疏和密集的损失值
        loss_sparse = loss_criterion(output_reshape[a_output_indices].view(-1, 1), Y[a_Y_indices].view(-1, 1))
        loss_dense = loss_criterion(output_reshape[~a_output_indices].view(-1, 1), Y[~a_Y_indices].view(-1, 1))
        loss = (loss_sparse + loss_dense)* 0.01
    else:
        loss = loss_criterion(output_reshape, Y.view(-1, 1)) * 0.01

六 实验部分

综合实验效果对比 

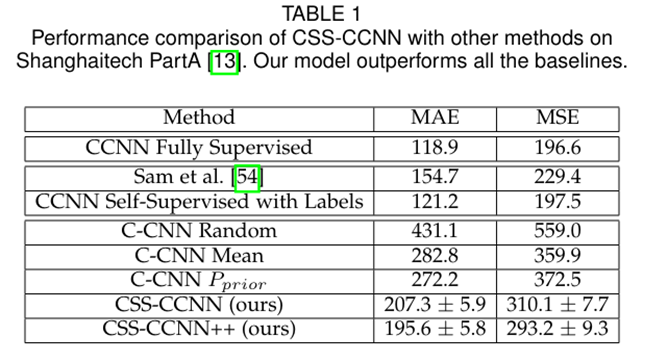
如表1所示，CSS-CCNN模型在三次独立实验（不同初始化条件下）中均显著优于所有基线方法，其平均性能指标及方差结果验证了方法的稳定性。相较于不考虑图像内容的简单策略，该方法展现出明显优势。改进后的CSS-CCNN++版本通过更精确的Sinkhorn匹配过程，将计数误差进一步降低约5%。值得注意的是，仅使用旋转自监督训练的CCNN网络性能已超越之前提出的模型。更引人注目的是，CSS-CCNN的计数精度（MAE指标）甚至优于早期部分全监督方法的性能水平。

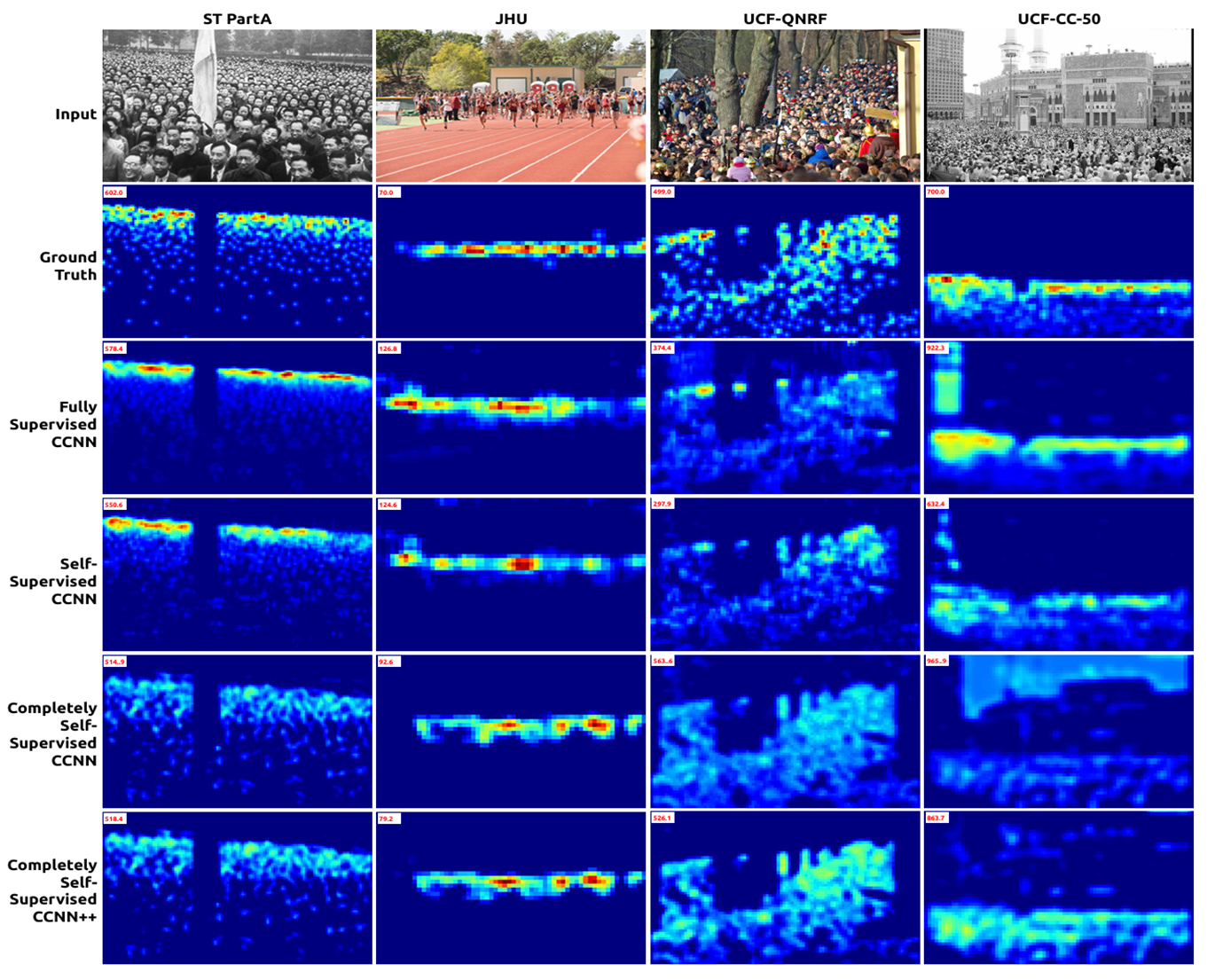
 不同数据集效果对比

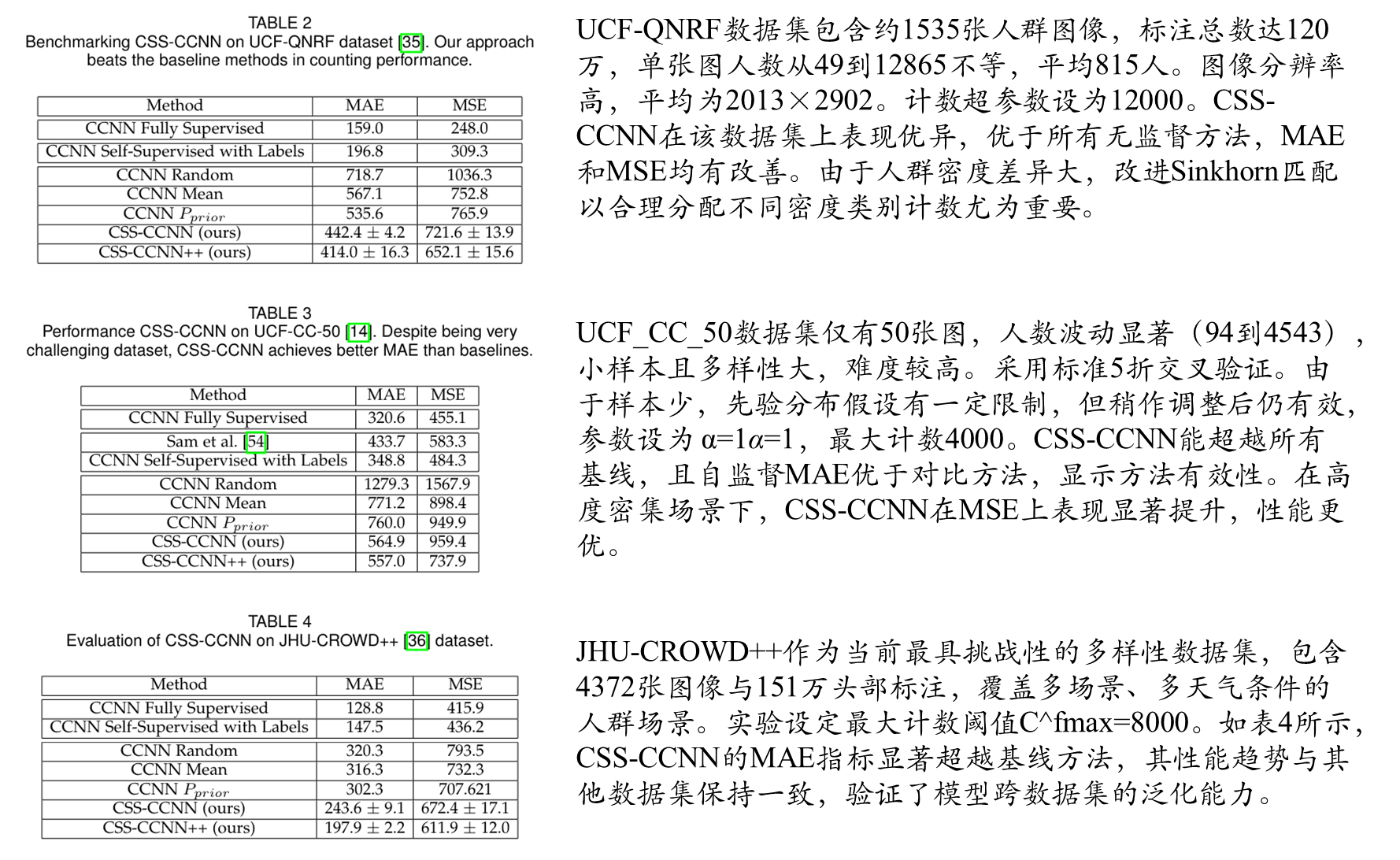
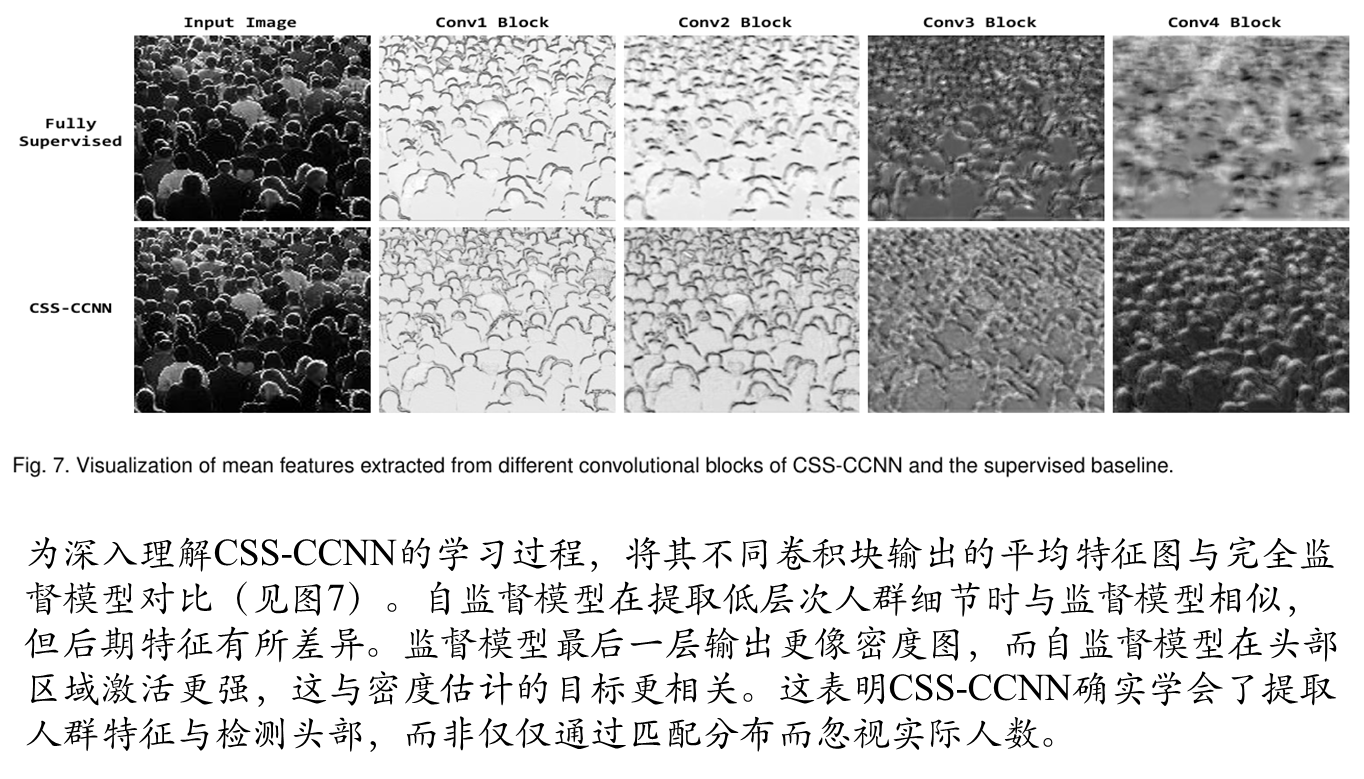
全监督和完全自监督

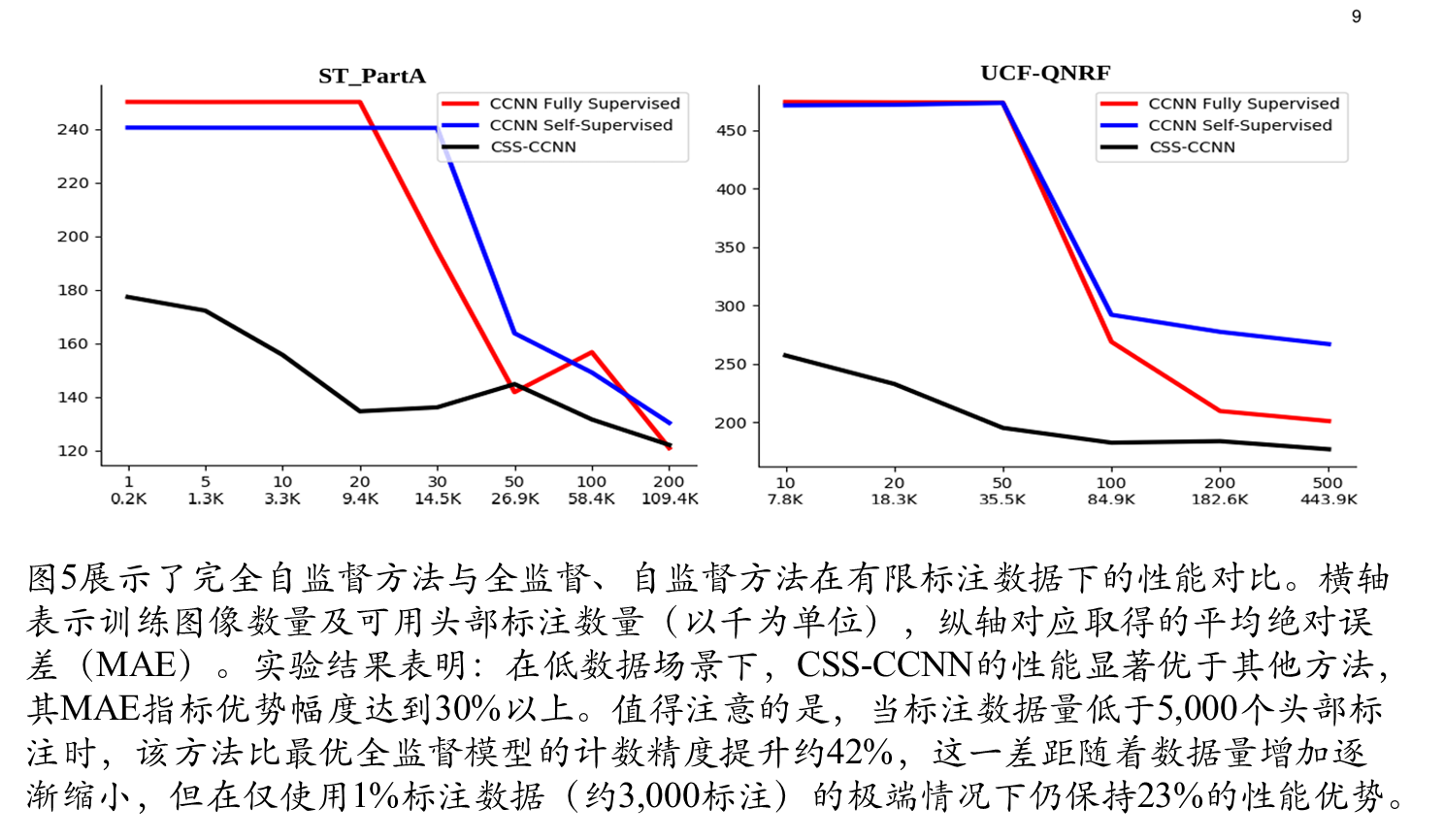
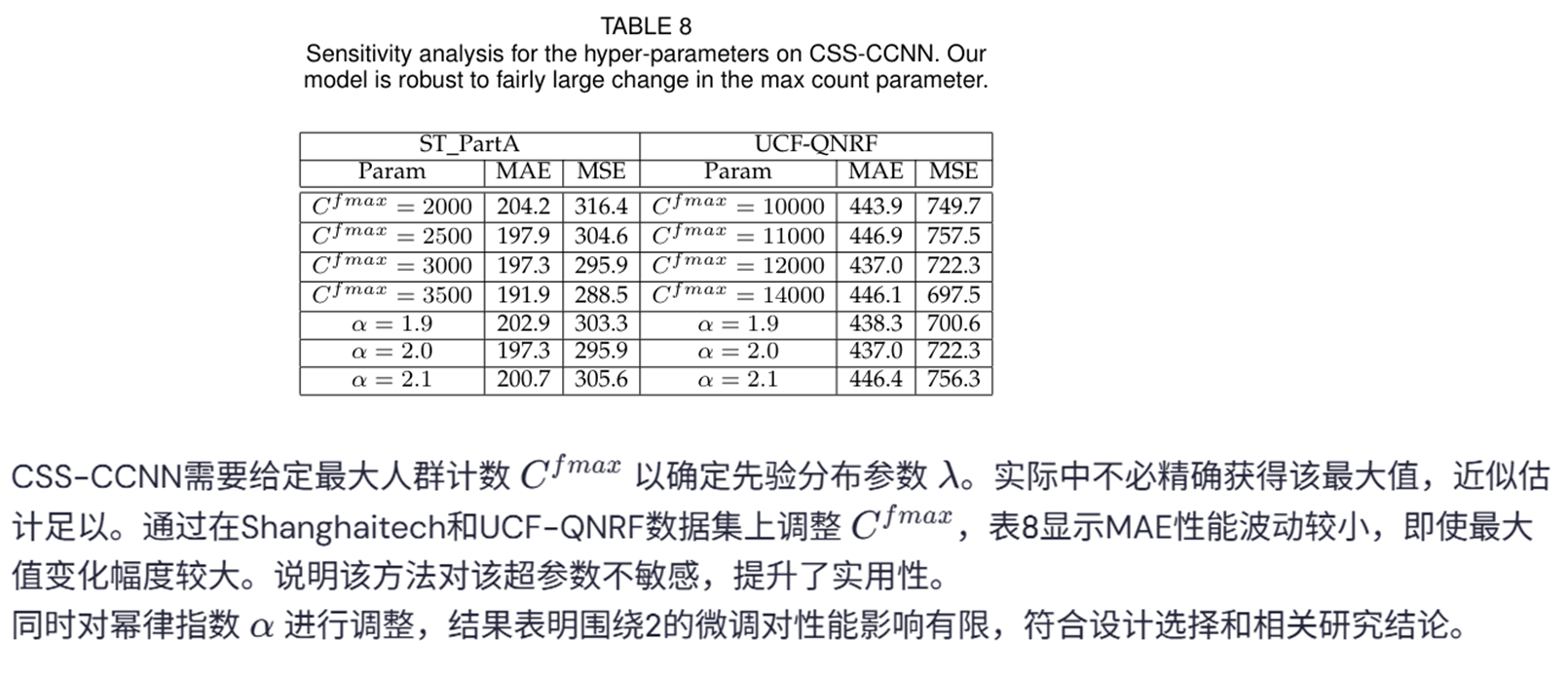
消融实验

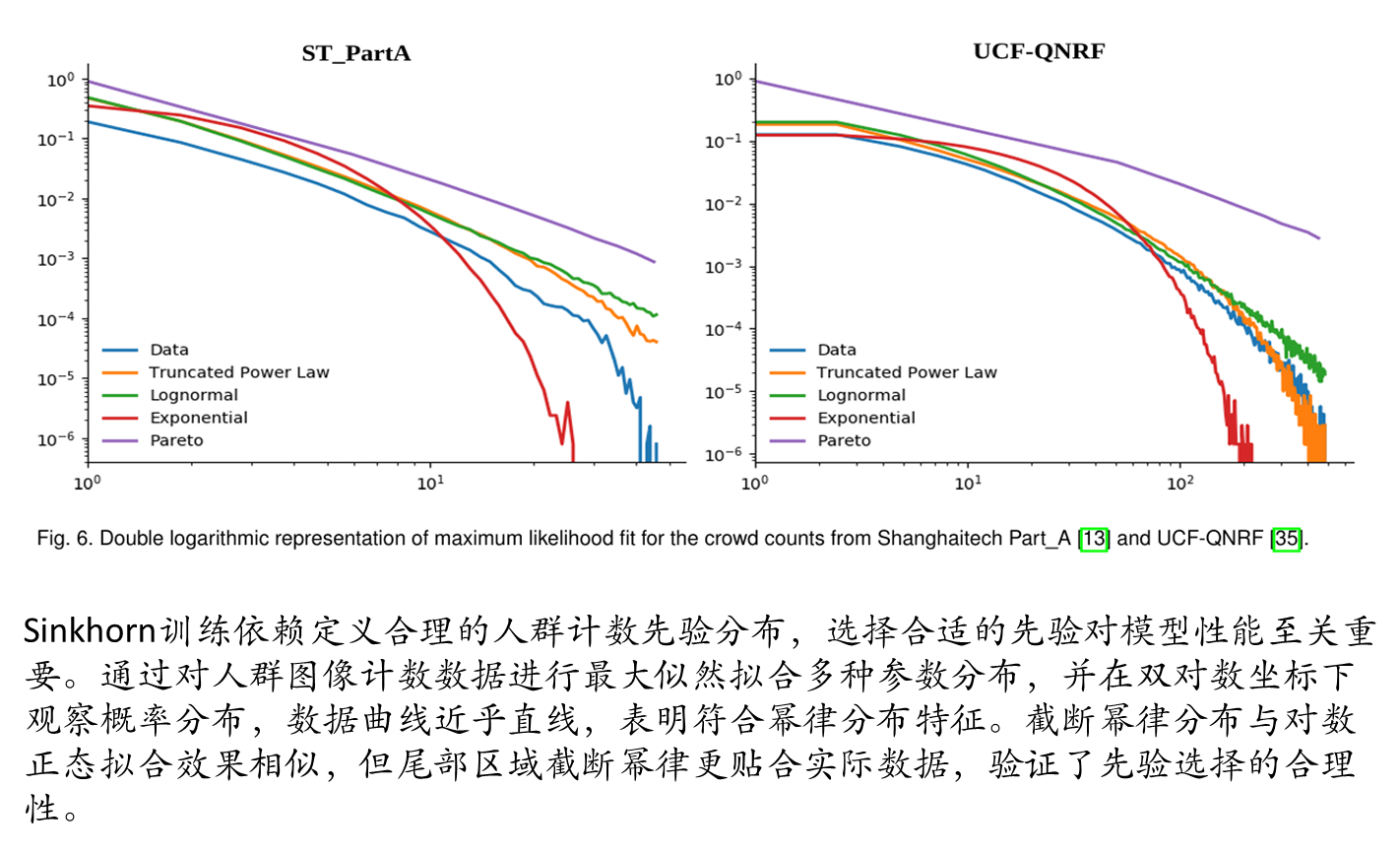
不同先验选择