弹簧阻尼系统与谐振电路的相似性

参考链接：

【振动中的数学——谐振频率】 https://www.bilibili.com/video/BV1dL411N7PB/?share_source=copy_web&vd_source=59b3c27bd034b606c96ffb3b7707f893

机械振动系统与RLC谐振电路的类比分析

在物理学与工程学中，看似迥异的系统——如弹簧-质量-阻尼构成的机械振动系统与由电阻（R）、电感（L）和电容（C）组成的电路——却在数学本质和动态行为上展现出惊人的相似性。这种相似性不仅体现了自然规律的统一性，也为跨领域建模与分析提供了有力工具。本文从数学模型、谐振条件、阻尼效应和工程应用四个维度，系统阐述两类系统的类比关系。

---

一、数学模型的对应性

两类系统均可由二阶线性常微分方程描述，具有完全相同的数学结构。

1. 机械系统（弹簧-质量-阻尼器）

考虑一个质量为 m 的物体连接在弹簧（劲度系数 k ）和阻尼器（阻尼系数 c ）上，受外力 F(t) 驱动，其运动方程为：

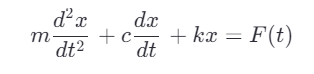
其中：

• x(t) ：位移（m）
• m ：质量（kg）
• c ：阻尼系数（N·s/m）
• k ：弹簧刚度（N/m）

2. 电路系统（RLC串联电路）

在RLC串联电路中，设外加电压为 V(t) ，电荷量为 q(t) ，电流 i=dq/dt ，则电路方程为：

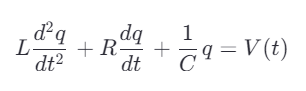
其中：

• q(t) ：电荷（C）
• L ：电感（H）
• R ：电阻（Ω）
• C ：电容（F）

3. 机电类比对应关系

机械系统	RLC电路系统
位移x	电荷q
速度x˙	电流i=q˙​
质量m	电感L
阻尼系数c	电阻R
弹簧刚度k	1/电容1/C
外力F(t)	外加电压V(t)

由此可知，机械位移 ↔ 电荷，力 ↔ 电压，构成“力-电压类比”（也称“直接类比”）。

---

二、谐振条件的共性

两类系统在无外力（或无源）自由振动时，均存在一个固有角频率（natural angular frequency），当系统参数匹配时，能量在两种储能元件间高效交换，形成谐振。

2. 能量转换机制

• 机械系统：
  动能 21​mv2 与弹性势能 21​kx2 周期性转换，阻尼器（如摩擦）以热能形式耗散能量。

• RLC电路：
  磁场能 21​Li2 （储于电感）与电场能 21​Cq2​ （储于电容）交替转换，电阻以焦耳热形式耗散能量。

这种储能-释能-耗能的循环，正是两类系统产生振荡行为的物理根源。

---

三、阻尼效应的类比

实际系统中总存在能量损耗，导致振幅逐渐衰减。阻尼程度决定系统响应类型（欠阻尼、临界阻尼、过阻尼）。

1. 阻尼比（Damping Ratio）

两类系统均可引入无量纲阻尼比 ζ 来描述阻尼强度：

• 机械系统：

ζ=2mk​c​

• RLC电路：

ζ=2R​LC​​=2R​⋅ω0​L1​

当 ζ<1 ：系统**欠阻尼**，呈现衰减振荡；
当 ζ=1 ：**临界阻尼**，最快回到平衡无振荡；
当 ζ>1 ：过阻尼，缓慢回归无振荡。

2. 品质因数（Q Factor）

衡量系统“选择性”或“振荡持久性”的指标：

Q=2ζ1​=Δωω0​​

• 机械系统：高Q值表示低阻尼，振荡衰减慢（如音叉）；
• 电路系统：高Q值表示窄带滤波特性（如收音机选频电路）。

---

四、工程应用的互通性

由于数学与物理机制的高度相似，两类系统的分析方法可相互迁移，推动跨学科技术创新。

应用领域	机械系统实例	电路系统实例
故障诊断	通过结构固有频率变化检测裂纹	输电线路故障定位（行波+谐振分析）
滤波与选频	减振器设计（避开共振频率）	RLC带通/带阻滤波器（如中频放大器）
传感器与换能器	加速度计（质量-弹簧系统）	振荡器、LC谐振传感器（如无线充电）
能量回收	振动能收集装置	无线能量传输中的谐振耦合

例如，在高压输电线路中，利用线路分布参数形成的等效LC网络，其自由振荡频率可反映线路长度或故障点位置，这与机械结构中通过模态分析定位损伤的原理如出一辙。