【算法】单调栈

最新推荐文章于 2025-11-27 16:11:46 发布

原创最新推荐文章于 2025-11-27 16:11:46 发布 · 6.7k 阅读

28 ·

CC 4.0 BY-SA版权

文章标签：

#算法

题解同时被 2 个专栏收录

19 篇文章

订阅专栏

算法

5 篇文章

订阅专栏

本文详细介绍了单调栈的概念、伪代码以及在不同问题中的应用，包括模板题、视野总和问题、柱状图中的最大矩形和最大区间问题的解题思路和代码实现。通过实例展示了单调栈如何帮助解决复杂问题，并提供了相应的算法优化技巧。

单调栈的定义：

从名字上就能猜出来，这种数据结构在栈的基础上，栈内的元素是单调有序的，所以单调栈分为单调递增栈和单调递减栈（增减性的划分是根据栈顶到栈底的元素变化规律）~~（搞不懂为什么定义要从栈顶开始看，栈是从栈底开始加入元素的呀，好像有一点反思维）~~

单调递增栈：从栈顶往栈底看，是单调递增的关系（含相等）
单调递减栈：从栈顶往栈底看，是单调递减的关系（含相等）

例子：现在有一组数：3，4，2，6，4，5，2，3，如果从左往右依次进单调递增栈，那么是这样操作的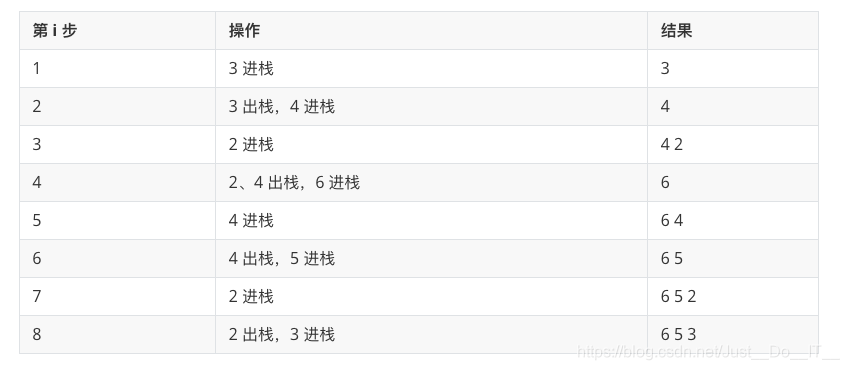：在这里插入图片描述

伪代码：

以单调递增栈为例：

stack<int> st;
//此处一般需要给数组最后添加结束标志符
for (遍历这个数组)
{
	// 如果栈不为空且栈顶元素比压栈元素小，则栈顶元素出栈并作计算与更新结果，然后继续下一轮比较，直至该元素可以入栈；
    // 否则，（即栈为空，或栈顶元素大于等于压栈元素），直接入栈即可
    while ( !st.empty() && vec[st.top()] < vec[i] ) {
        st.pop();
        // Do something
    }
    st.push(i);  // 数组内的元素都要入栈，但入栈的是其下标
}

注意事项：

为了保证栈内元素最后都能出栈，需要在数组结尾添加一个特殊的数字：
对单调递增栈，在数组末尾添加一个最大数，如 INT_MAX; 对单调递减栈，在数组末尾添加一个最小数，如 INT_MIN.
数组中的所有元素都要入栈一次和出栈一次，除了最后一个特殊元素；
当一个元素出栈的时候，做计算，更新答案；
当一个元素即将出栈时，记住整个栈内元素具有单调性，很多时候需要利用这个特性去做计算；
一个元素可能会令栈中若干个元素出栈，但也可能是直接入栈

应用

1.模板题

洛谷P5788 【模板】单调栈

题目：
在这里插入图片描述
解题思路：
求每个数后第一个大于他的数。
直接看数字不太容易想，那么我们把题目转化一下：有 $n$ 个人，每个人向右上方看，求她看到的第一个人。

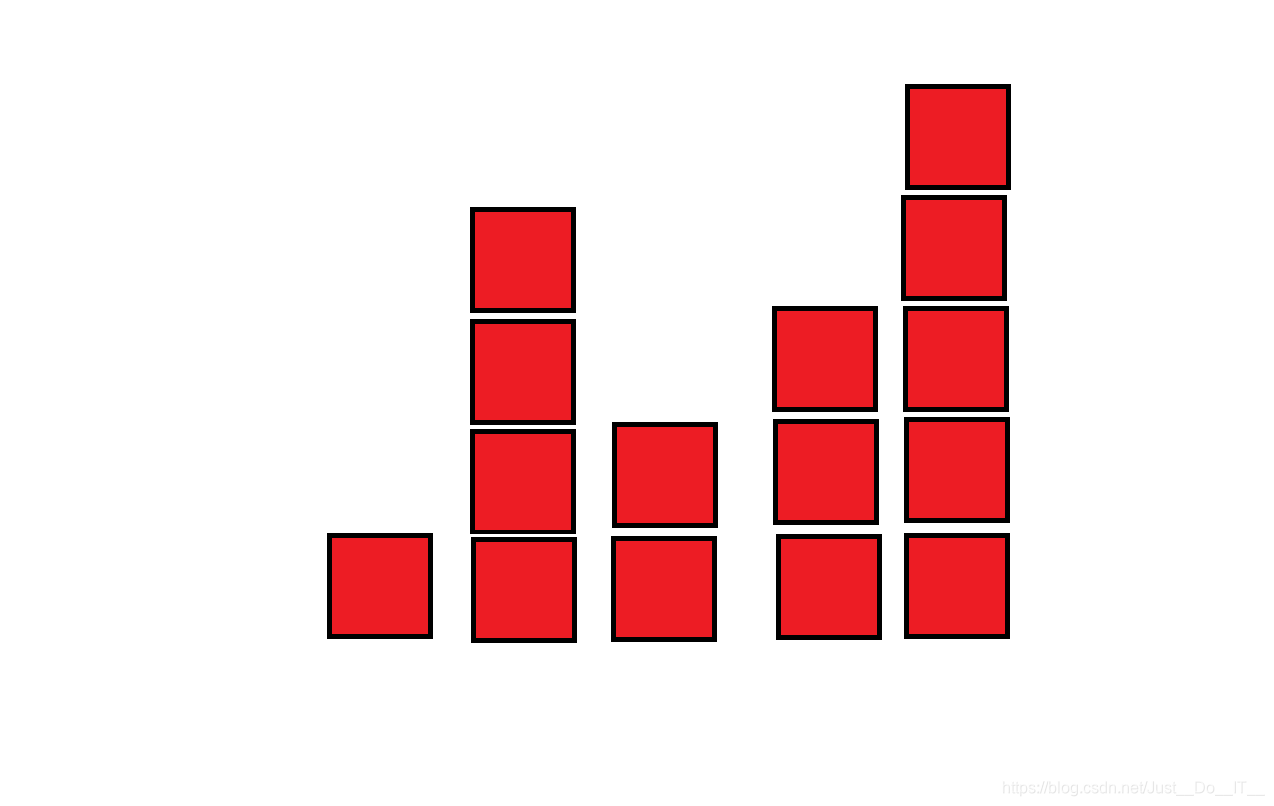
比如第2个人，他的高度是4，那么他往右上方看，肯定看不到第3，第4个人，因为他们比他矮，被遮住了，那留着也没用，直接舍弃就好（我没有歧视矮，我也想长高QwQ）。那么大家是否看到了单调性？比他矮的人全部舍弃，留下的都是比他高的。所以我们可以用单调栈实现。由于是往右看，所以需要从后往前遍历数组。

代码：

#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 3e6 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int a[MAXN],ans[MAXN];
stack<int> s;//单调递增栈 

int main()
{
	qc;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i]; 
	for(int i=n;i>0;i--)
	{
		while(!s.empty() && a[s.top()]<=a[i])
			s.pop();
		ans[i]=s.empty()? 0:s.top();
		s.push(i);//压入下标
	}
	for(int i=1;i<n;i++)
		cout<<ans[i]<<" ";
	cout<<ans[n]<<endl;
	return 0;
}

2.视野总和问题

POJ-3250 Bad Hair Day

题目：
在这里插入图片描述

题目大意：
一群高度不完全相同的牛从左到右站成一排，每头牛只能看见它右边的比它矮的牛的发型，若遇到一头高度大于或等于它的牛，则无法继续看到这头牛和后面的其他牛的发型。给出这些牛的高度，要求每头牛可以看到的牛的数量的和。

解题思路1：
每个元素只会出栈一次，所以当他出栈的时候就可以计算出他可以看到的牛的个数了，即当前所在下标与自己下标的差值。

代码1：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stack>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 3e6 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int a[MAXN];
stack<int> s;//单调栈 

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i]; 
	n++;
	a[n]=inf;
	ll ans=0;//千万记得开ll,不然就像我一样，debug一个小时，QwQ
	for(int i=1;i<=n;i++)
	{
		while(!s.empty() && a[s.top()]<=a[i])
		{
			ans+=(i-s.top()-1);
			s.pop();
		}	
		s.push(i);
	}
	cout<<ans<<endl;
	return 0;
}

解题思路2：（一开始找不到第一个思路的bug时，看其他博客的思路找到的）
可以把问题等效成每头牛可以被看到的次数之和。
构建一个单调递增栈，栈底元素最大，从左到右依次读取牛的高度，当待入栈元素小于栈顶元素时，代表目前栈里的牛都可以看到这头牛，答案加上目前栈里的元素的个数，然后把该元素入栈，继续下一个比较；如果待入栈元素大于等于栈顶元素时，就要从栈中弹出比它小的，即删除不能看到这头牛的元素，答案加上目前栈里所剩元素的个数，然后把该元素入栈，继续下一个比较。注意！当你计算栈中元素个数时，要记得减去特殊元素哦！！！

代码2：

#include <iostream>
#include <string.h>
#include <algorithm>
#include <stack>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 80000 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int a[MAXN];
stack<int> s;//单调栈 

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	int n;
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i]; 
	s.push(inf);//压入特殊元素 
	ll ans=0;
	for(int i=1;i<=n;i++)
	{
		while(!s.empty() && s.top()<=a[i])
		{
			s.pop();
		}
		ans+=(s.size()-1);//有一个特殊元素要减去 
		s.push(a[i]);
	}
	cout<<ans<<endl;
	return 0;
}

3.柱状图中的最大矩形

Acwing 131. 直方图中最大的矩形

题目：
在这里插入图片描述

解题思路：
维护一个单调递减栈，即从栈底到栈顶依次增大，这样栈中的元素往右扩展，一定可以成为更大的矩形。如题目中的图所示，当该元素要被弹出栈的时候，那么就可以计算以该元素为高往右最大扩展的矩形的面积了。计算出面积后，一直更新最大值，答案就出来了。

代码：

#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 2e5 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
vector<int> heights;

ll largestRectangleArea() 
{
    heights.push_back(INT_MIN);//特殊元素 
    ll result = 0;
    stack<int> st;
    
    ll h=0, w=0;
    int top_id = 0;

    for (int i=0; i<heights.size(); ++i)
    {
        // 单调栈内元素是递增的 
        while ( !st.empty() && heights[st.top()] > heights[i] ) {
            top_id = st.top();
            st.pop();
            h = heights[top_id];
            if (st.empty()) //栈为空，代表是目前最小的，所以0~i-1所有都可以满足 
                w = i;
            else 
                w = i - st.top() - 1;//i：将要入栈的下标，st.top():下一个可能出栈的元素小标 
      
            result = max(result, w*h);
        }
        st.push(i);
    }
    return result;
}

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	int n,tmp;
	while(cin>>n)
	{
		if(n==0)
			break;
		while(!heights.empty())//清空vector 
			heights.pop_back();
		for(int i=0;i<n;i++)
		{
			cin>>tmp;
			heights.push_back(tmp);
		}
		ll ans=largestRectangleArea();
		cout<<ans<<endl;
	} 
	return 0;
}

题目变形：

洛谷 P4147 玉蟾宫

解题思路：

按行去划分，O(n)枚举每一行，对该行即以上的部分做最大子矩阵处理；
用pos数组记录每行向上可延伸的最大距离，预处理的方式为：
(1)读到一个‘F’，该处pos=上一行该列pos的值+1；
(2)读到一个‘R’，该处pos=0（因为该处不可向上伸展）；

代码：

#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 2e5 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
int n,m,pos[1010][1010],maxs=0;
ll ans;
vector<int> heights;

ll largestRectangleArea(int k) 
{
	while(!heights.empty())
		heights.pop_back();
	for(int i=1;i<=m;i++)
		heights.push_back(pos[k][i]);
    heights.push_back(INT_MIN);//特殊元素 
    ll result = 0;
    stack<int> st;
    ll h=0, w=0;
    int top_id = 0;

    for (int i=0; i<heights.size(); ++i)
    {
        // 单调栈内元素是递增的 
        while ( !st.empty() && heights[st.top()] > heights[i] ) {
            top_id = st.top();
            st.pop();
            h = heights[top_id];
            if (st.empty()) //栈为空，代表是目前最小的，所以0~i-1所有都可以满足 
                w = i;
            else 
                w = i - st.top() - 1;//i：将要入栈的下标，st.top():下一个可能出栈的元素小标 
      
            result = max(result, w*h);
        }
        st.push(i);
    }
    return result;
}

int main()
{
//	freopen("in.txt", "r", stdin);
	qc;
	char c;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>c;
			if(c=='F')
				pos[i][j]=pos[i-1][j]+1;
		}
	}
	ll tmp=0;
	for(int i=1;i<=n;i++)
	{
		tmp=largestRectangleArea(i);
		ans=max(tmp,ans);
	}
	cout<<3*ans<<endl;
	return 0;
}

4.最大区间

POJ 2796 Feel Good

题目：
在这里插入图片描述

题目大意：

给你一组数字，求一区间，使得区间元素和乘以区间最小值最大，结果要求输出这个最大值和区间的左右端点

解题思路：
首先应该能想到暴力的做法。想要求出答案，那么对于每一个以 $a_i$ 为最小的元素的区间，它的左右端点都是比它小的数(为了方便，用开区间来描述)。所以只要以 $a_i$ 的起点向左右扩展就行了，这样的复杂度是 $O(n^2)$ 。
那么如何来优化呢？计算区间的和用前缀和就行了，那么区间的端点呢？可以用单调栈来解决。我们用单调栈来维护区间最小值，那么对当前元素来说，在它之前的一个最小值和在它之后的一个最小值就是区间的两个端点。所以我们用一个单调递增栈从前到后面扫一遍，就求出 $a_i$ 左边比 $a_i$ 小的一个元素，同样倒着扫一遍就能求出另一边的元素。

代码：

//#include <bits/stdc++.h>
#include <iostream>
#include <string.h>
#include <algorithm>
#include <stack>
#define ll long long
#define qc ios::sync_with_stdio(false); cin.tie(0);cout.tie(0)
using namespace std;
const int MAXN = 1e5 + 7;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const int N=1e5+100;
const int maxn = 1e5+10;
ll arr[MAXN], pre[MAXN];
int n, l[MAXN], r[MAXN];
stack<int> st;
int main() {
    scanf("%d", &n);
    for (int i = 1; i<=n; ++i) {
        scanf("%lld", &arr[i]);
        pre[i] += pre[i-1]+arr[i];
    }
    for (int i = 1; i<=n; ++i) {
        while(!st.empty() && arr[st.top()]>=arr[i]) st.pop();
        l[i] = st.empty() ? 1 : st.top()+1;
        st.push(i);
    }
    while(!st.empty()) st.pop();
    for (int i = n; i>=1; --i) {
        while(!st.empty() && arr[st.top()]>=arr[i]) st.pop();
        r[i] = st.empty() ? n : st.top()-1;
        st.push(i);
    }
    ll maxx = -1; 
	int pl,pr;
    for (int i = 1; i<=n; ++i)
        if (maxx < (ll)arr[i]*(pre[r[i]]-pre[l[i]-1])) {
            maxx = (ll)arr[i]*(pre[r[i]]-pre[l[i]-1]);
            pl=l[i];
			pr=r[i];
        }
    cout << maxx << "\n" << pl << " " << pr << endl; 
    return 0;
}