一、前言
二叉树是数据结构中的核心概念,其“左小右大”的特性使其在查找、插入、删除操作中具有高效性能。本文将通过数组(顺序存储) 实现二叉树的构建,并配套实现前序、中序、后序三种递归遍历方式,代码简洁易懂。
二、核心思路
1. 数组存储二叉树的优势
无需额外定义节点结构体,通过数组下标直接映射节点关系:
· 根节点存于下标 1(避免下标0导致子节点计算冲突)
· 若节点下标为 index ,则左子下标为 index*2 ,右子下标为 index*2+1
· 初始化简单,用 0 表示空节点,直观易理解
2. 二叉树构建规则
· 以数组第一个元素作为根节点
· 后续元素按“左小右大”原则插入:
· 新节点值 < 当前节点值 → 插入左子树
· 新节点值 ≥ 当前节点值 → 插入右子树
· 通过循环从根节点开始查找空位置,找到后完成插入
3. 三种遍历逻辑
· 前序遍历:根 → 左子树 → 右子树
· 中序遍历:左子树 → 根 → 右子树
· 后序遍历:左子树 → 右子树 → 根
三、完整代码实现
1. 头文件与定义
#include <stdio.h>
#include <stdlib.h>
#define MAX_SIZE 100 // 二叉树数组最大容量(可根据需要调整)2. 遍历函数
· 前序遍历
// 前序遍历(根、左、右)
void preOrder(int mybtree[], int index, int maxIndex) {
if (index > maxIndex || mybtree[index] == 0) {
return;
}
printf("%d ", mybtree[index]); // 访问根
preOrder(mybtree, index*2, maxIndex); // 遍历左子树
preOrder(mybtree, index*2+1, maxIndex); // 遍历右子树
}· 中序遍历
// 中序遍历(左、根、右)
void inOrder(int mybtree[], int index, int maxIndex) {
if (index > maxIndex || mybtree[index] == 0) {
return;
}
inOrder(mybtree, index*2, maxIndex); // 遍历左子树
printf("%d ", mybtree[index]); // 访问根
inOrder(mybtree, index*2+1, maxIndex); // 遍历右子树
}· 后序遍历
// 后序遍历(左、右、根)
void postOrder(int mybtree[], int index, int maxIndex) {
if (index > maxIndex || mybtree[index] == 0) {
return;
}
postOrder(mybtree, index*2, maxIndex); // 遍历左子树
postOrder(mybtree, index*2+1, maxIndex); // 遍历右子树
printf("%d ", mybtree[index]); // 访问根
}3. 主函数main入口
int main() {
int nodelist[] = {6, 3, 8, 5, 2, 9, 4, 7};
//动态计算节点数:数组总结点数 / 单个元素字节数
int len = sizeof(nodelist) / sizeof(nodelist[0]); // nodelist[0]——代表单个元素的字节大小
//初始化二叉树组:用0填充(0代表“空节点”)
int mybtree[MAX_SIZE] = {0};
int index, i; //index——记录当前插入位置,i——循环变量
// 构建二叉搜索树
mybtree[1] = nodelist[0]; //根节点存在下标1
for (i = 1; i < len; i++) {
//每次插入新节点,都从根节点(下标1)开始找位置
index = 1;
while (mybtree[index] != 0) {
if (mybtree[index] > nodelist[i]) {
index *= 2;
} else {
index = index*2 + 1;
}
}
mybtree[index] = nodelist[i];
}
// 遍历结果
printf("\n前序遍历:");
preOrder(mybtree, 1, 10); //从根节点(下标1)开始,遍历到下标10
printf("\n中序遍历:");
inOrder(mybtree, 1, 10);
printf("\n后序遍历:");
postOrder(mybtree, 1, 10);
printf("\n");
return 0;
}四、运行结果
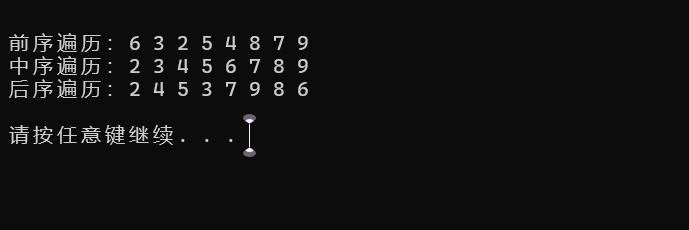
五、结语
本文通过数组实现了二叉搜索树的构建与遍历,代码简洁易懂,适合入门学习。数组存储的优势在于实现简单、节点关系直观,缺点是空间利用率较低,适用于节点数量较少的场景。若需处理大量数据,可进一步学习链式存储实现方式,详见:C语言数据结构-用链表的方式构建和遍历二叉树(前、中、后序)-优快云博客
 数组实现二叉树及遍历
数组实现二叉树及遍历






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








