MATLAB入门第二天

向量的创建

a=[1 3 5] or a=[1,3,5]

冒号法最常用：A:step:B

1:2:5

返回空向量的情况：

5:2:1  A>B且step>0;

10:-10:50  A<B且step<0;

1:0:2  step=0；

利用matlab函数创建

linspace创建等差数列

linspace(a,b)

向量中第一个元素为a，最后一个为b，总数为100

linspace(a,b,n)

向量中第一个元素为a，最后一个为b，总数为n

logspace创建等比数列

logspace(a,b)

第一个数是，最后一个数是，加上n就是n个数

logspace(log10(2),log10(1024),10)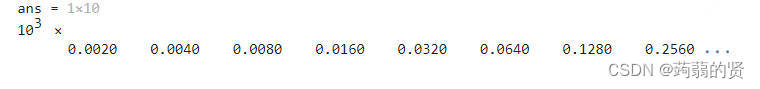

向量元素提取

向量元素个数计算

用函数length或numel

提取时下标从1开始，如a=[1 3 5];a(1)=1;

多个元素的提取：a（ind）

ind中放入要提取的元素的下标

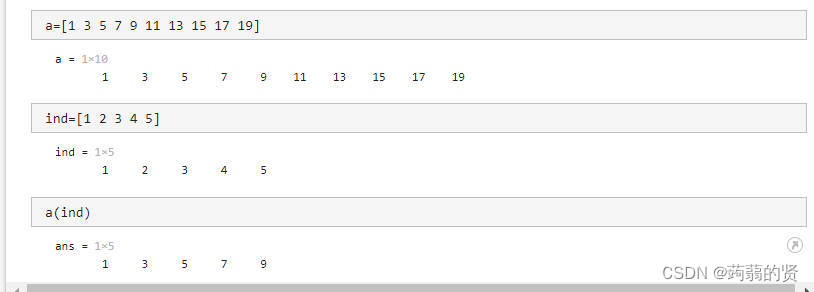
其他合理写法：a([1 2 3 4 5]),a(1:1:5)

end为最后一个元素

向量元素修改和删除

a(1)=4 第一个元素改为4

a([1 3])=[50 60] 第一个元素改为50，第二个元素改为60

a([1:3])=[50 60] 报错，元素个数不匹配

a([1 3 ])=100 指定位置的元素全变成100

a([end-1:end])=[] 删除倒数两个元素

补充：向量是特殊的矩阵，

如a=[1 2 3 4 5 6 7 8 9 ]

a([1,3])=1 3

a(1,3)不会报错，意思是第一行，第三列，即3

a(11)=1也不会报错，系统会把数组加到第11个，运行后为a=[1 2 3 4 5 6 7 8 9 0 1]

第10个元素未赋值，所以值为0

矩阵的创建

a=[]

同行用空格或逗号，换行用分号或回车键（matlab可以识别回车）

函数创建法

zeros：创建全为0的矩阵

a=zeros(3)  创建3行3列全0矩阵

a=zeros(m,n)  创建m行n列全0矩阵

ones：创建全为1的矩阵

eye：创建单位矩阵

主对角线元素为1，其他位置为0

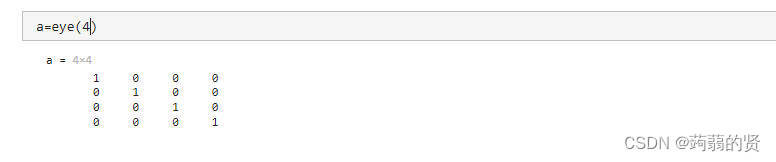
rand、randi、randn创建均匀分布的随机数、随机整数、标准正态分布的随机数

rand(m,n)  m行n列的0-1随机数矩阵

randi([imin,imax],m,n)  从向量[imin,imax]中随机生成m*n矩阵

如果imin=1，可以把向量直接写成imax

randn 0为均值，1为标准差

diag和blkdiag

diag创建对角矩阵

diag([1,2,3])

diag(v,k)  将v元素放到第k条对角线上

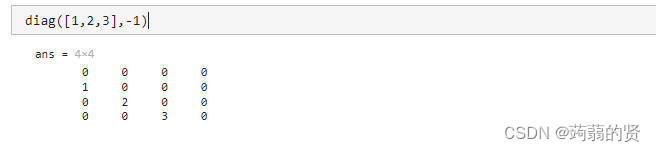
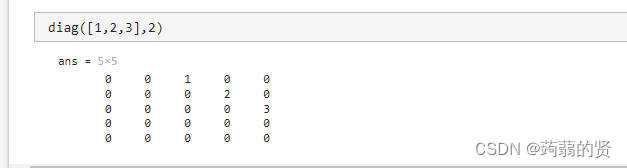若输入若输入的第一个参数为矩阵，则获取矩阵的对角线

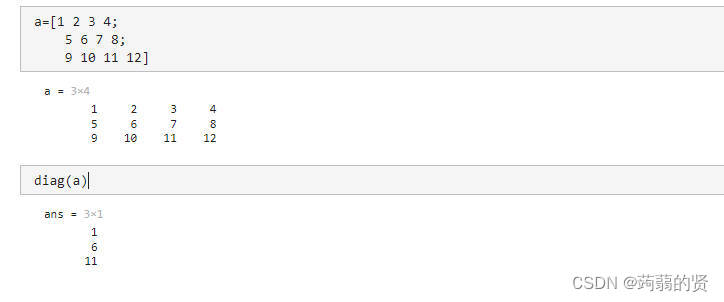diag(a,k)  获取a矩阵第k条对角线的元素

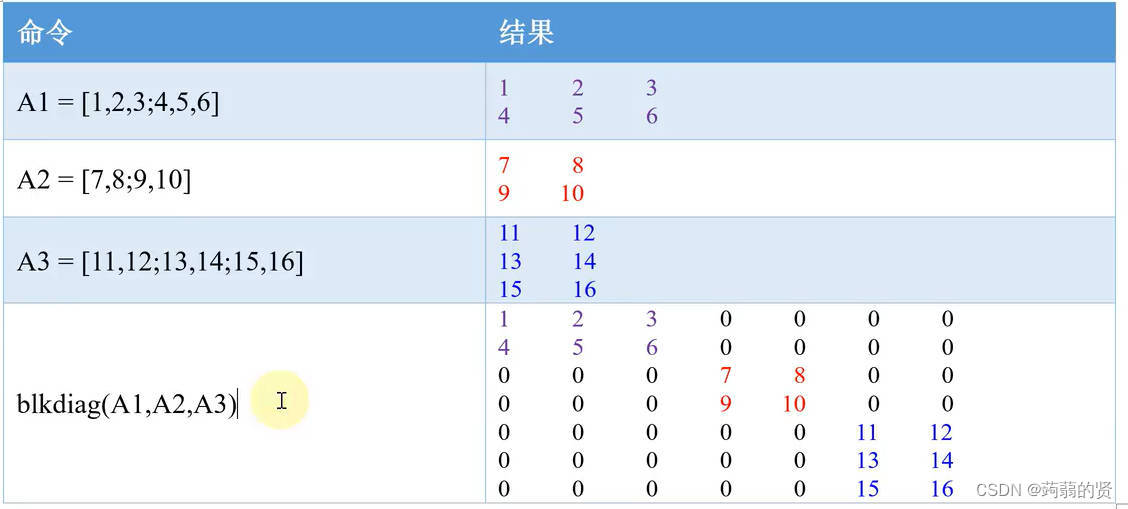
blkdiag创建分块对角矩阵

分块对角矩阵的对角线的元素是矩阵

矩阵元素提取

原始索引

a(1,2)	第一行，第二列的元素
a(2,end)	第二行，最后一列的元素
a(2,[1 3])	第二行，第一个、第三个元素
a(3,1:5)	第三行，1到5列的元素
a([1 3],[1 3 5])	第1、3行，第1、3、5个元素
a(1:2:end,1:2:end)	第奇数行，第奇数个元素
a(1,:)	第1行，所有列的元素

矩阵大小计算：size函数

size(A)返回值为一个行向量，如A为3*4的矩阵，则size返回[3 4]。

size(A,dim)返回A在dim维度的值，如size(A,1)=3,

length(A)返回值为A在所有维度中的最大值，numel返回所有元素的总和

线性索引

单下标的索引方法称为线性索引，矩阵在计算机中存储方式如下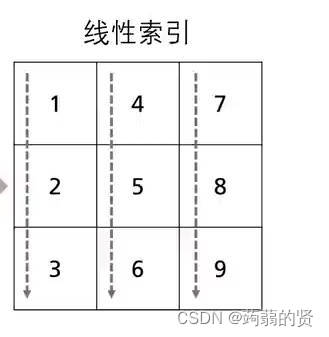

例如

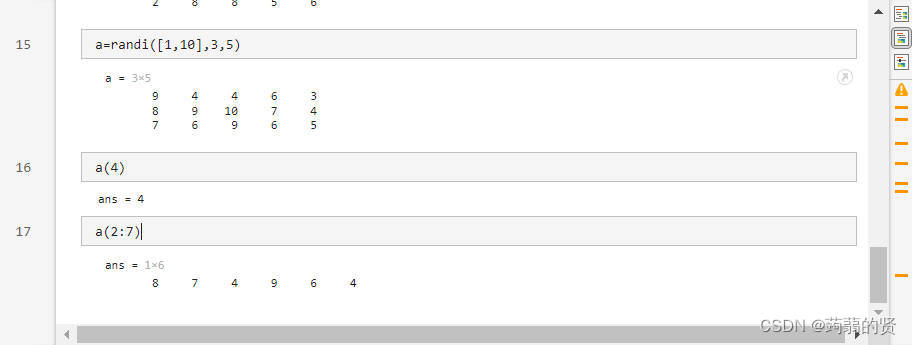
A(:)命令可以将A中的所有元素按照线性索引的顺序重构为一个列向量

两者的转换

 sub2ind和ind2sub函数

ind=sub2ind(sz,row,col)    sz为待转换矩阵

[row,col]=ind2sub(sz,ind)   ind为线性索引位置