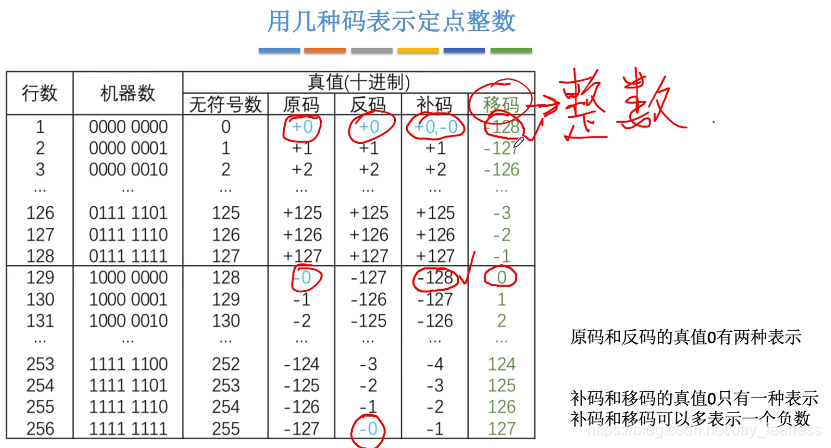
1.定点数
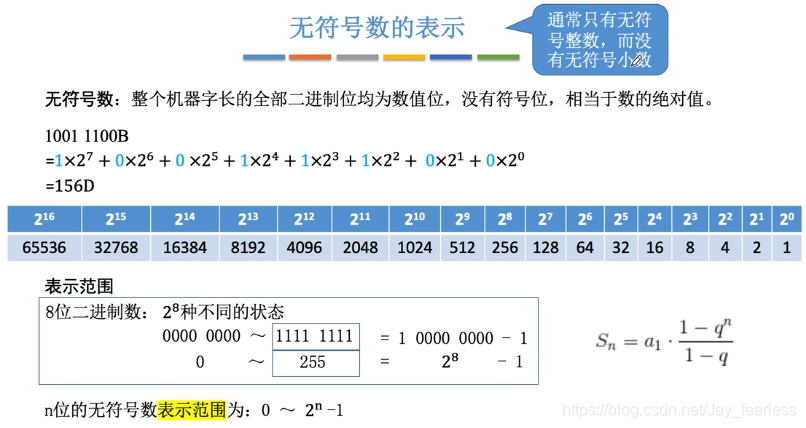
1.无符号数(unsigned)
n位的无符号数表示范围为: 0 ~ 2n−12^n-12n−1
2.有符号数(原、反、补、移)
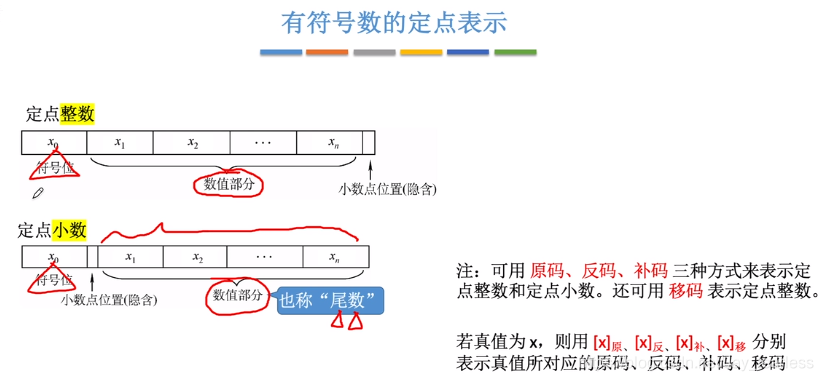
有符号数由符号值+数值部分(也称尾数部分)组成
0为正,1为负
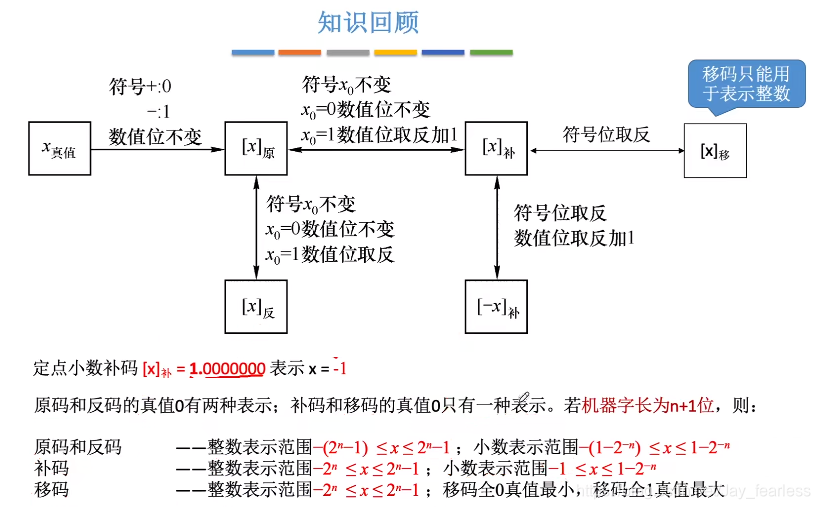
1.原码
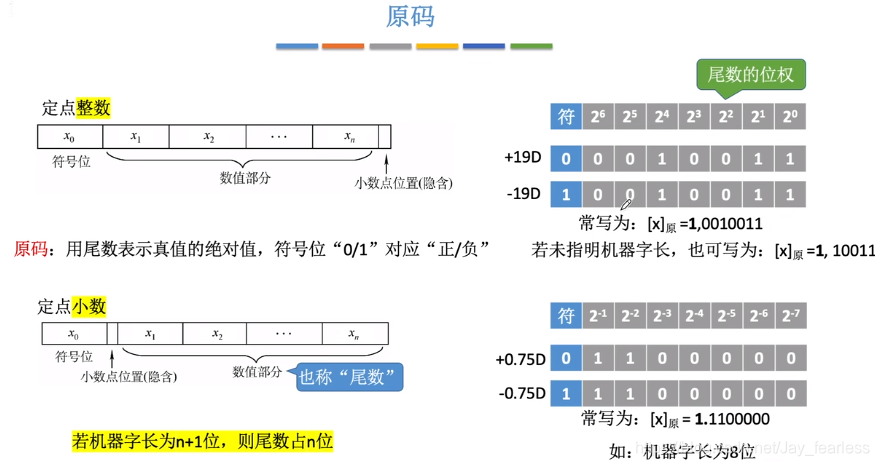
整数范围:n+1位 -(2n−12^n-12n−1)<=x<=2n−12^n-12n−1
小数范围:n+1位 -(1−2−n1-2^{-n}1−2−n)<=x<=1−2−n1-2^{-n}1−2−n

2.反码(整数、小数范围和原码一样)
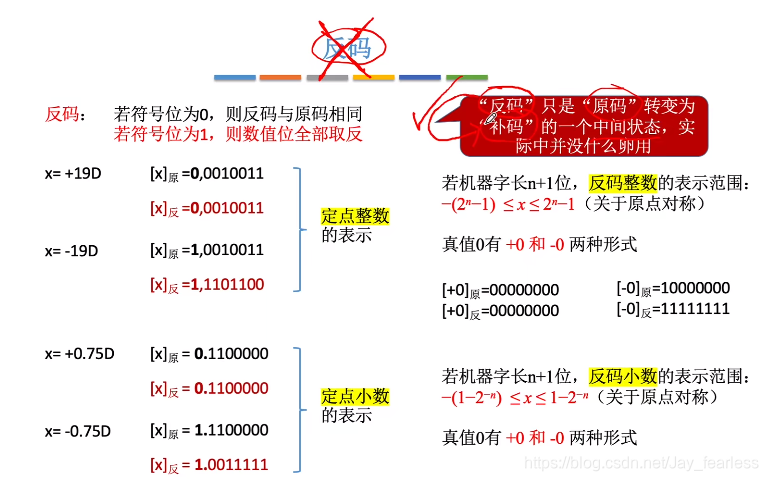
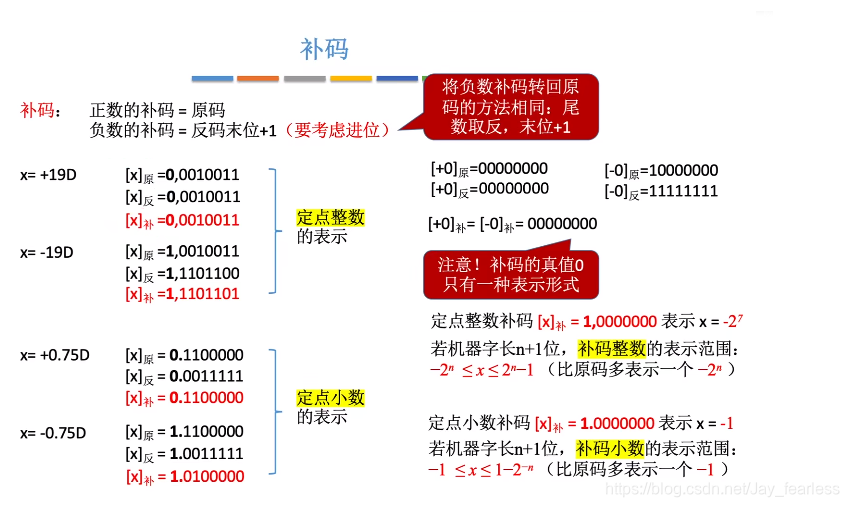
3.补码
将负数补码转回原码的方法相同:尾数取反,末位+1。
原理:补码的补码是原码。
为什么设计补码?
补码可以将减法操作转变为加法操作,节省硬件成本,ALU中无需集成减法器。
4.移码
补码的基础上将符号位取反。(**注意:**移码只能用于表示整数。)
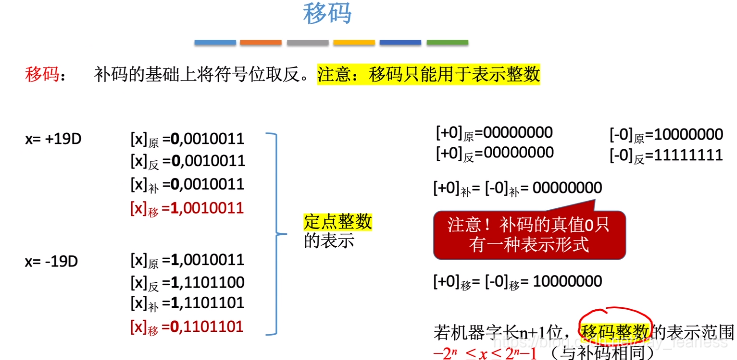
移码好处:方便计算机比较两个数的大小(两个数,谁先出现1,谁就比较大)
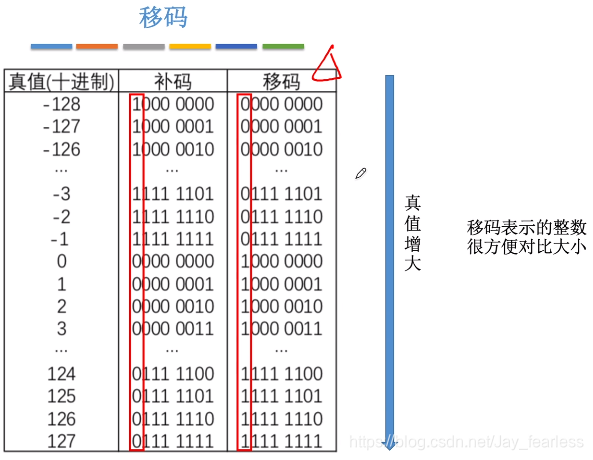
由[x]补求[−x]补方法[x]_{补}求[-x]_{补}方法[x]补求[−x]补方法:符号位、数值位全部取反,末位+1
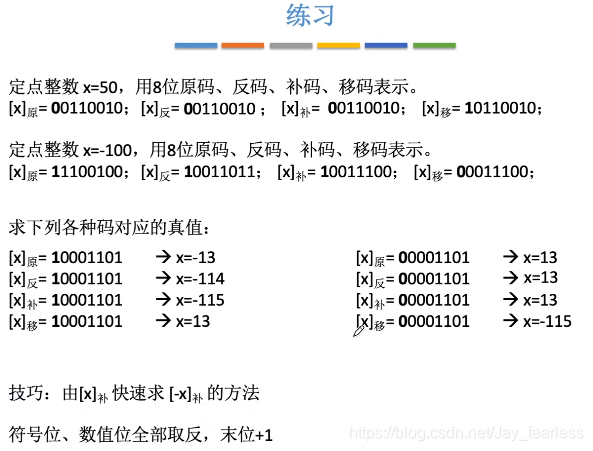
小结
2.移位运算
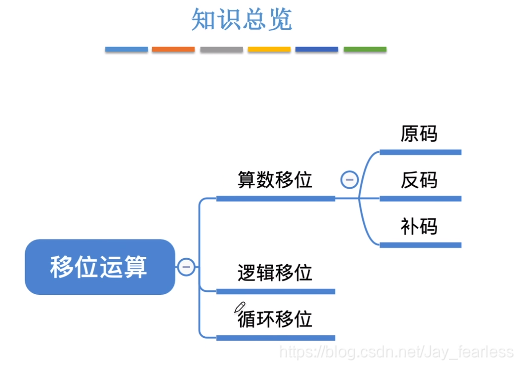
逻辑右移和算术右移
逻辑右移就是不考虑符号位,右移一位,左边补零即可。
算术右移需要考虑符号位,右移一位,若符号位为1,就在左边补1,;否则,就补0。
所以算术右移也可以进行有符号位的除法,右移,n位就等于除2的n次方。
例如,8位二进制数110011011100110111001101分别右移一位。
逻辑右移就是[0]1100110[0]1100110[0]1100110
算术右移就是[1]1100110[1]1100110[1]1100110
1.原码
算术右移可能出现丢失精度的问题
高位补0,低位舍弃。若舍弃的位为0,则相当于÷2;若舍弃的位≠0,则会丢失精度。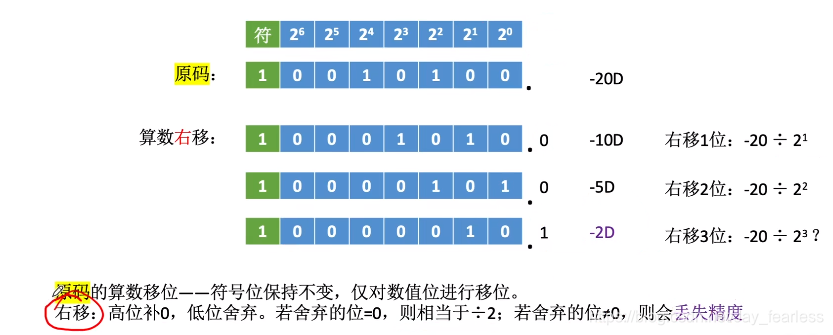
算术左移可能会出现严重误差
低位补0,高位舍弃。若舍弃的位=0,则相当于×2;若舍弃的位≠0,则会出现严重误差。
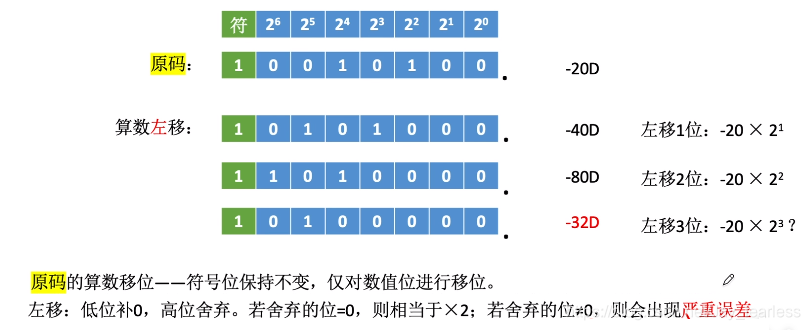
2.反码
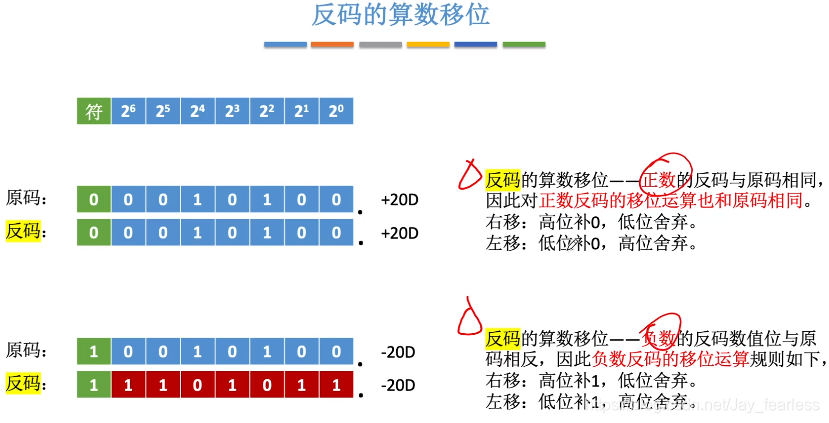
负数的反码数值位与原码相反,因此负数反码的移位运算规则如下:
右移:高位补1,低位舍弃。
左移:低位补1,高位舍弃。
3.加减运算和溢出判断
溢出判断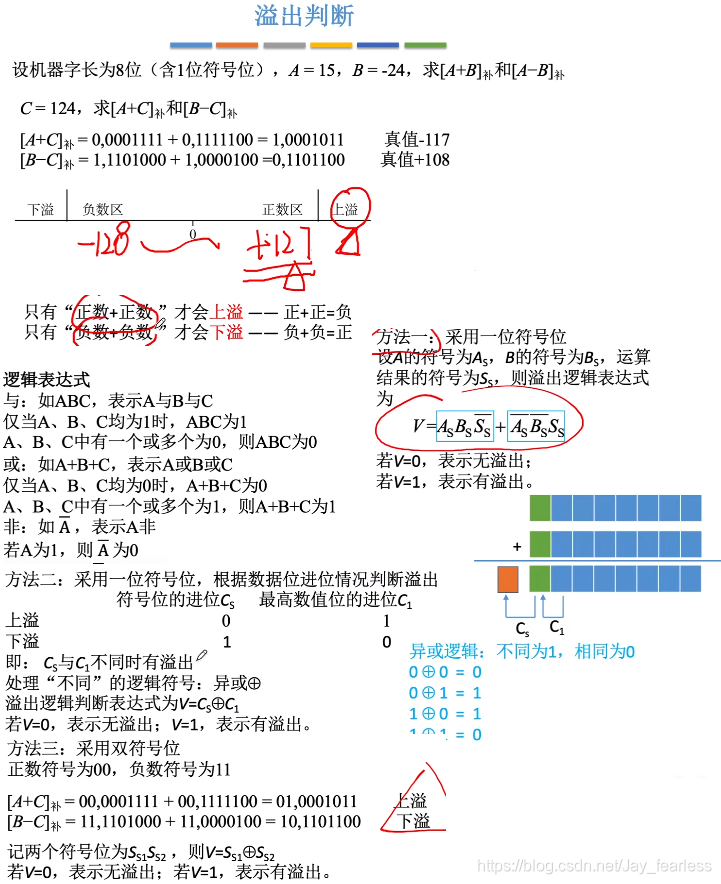
符号扩展int->long
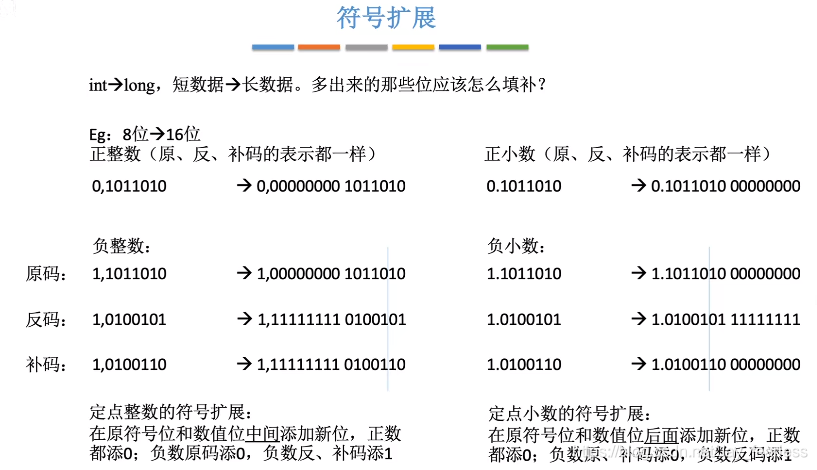
小结
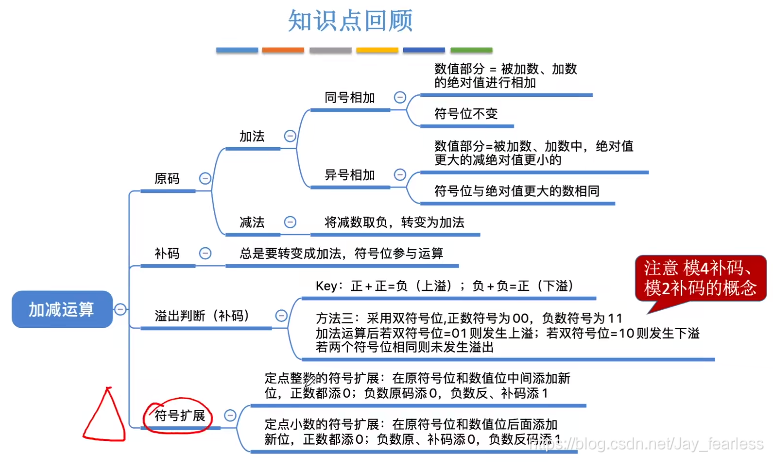
4.原码的乘法运算
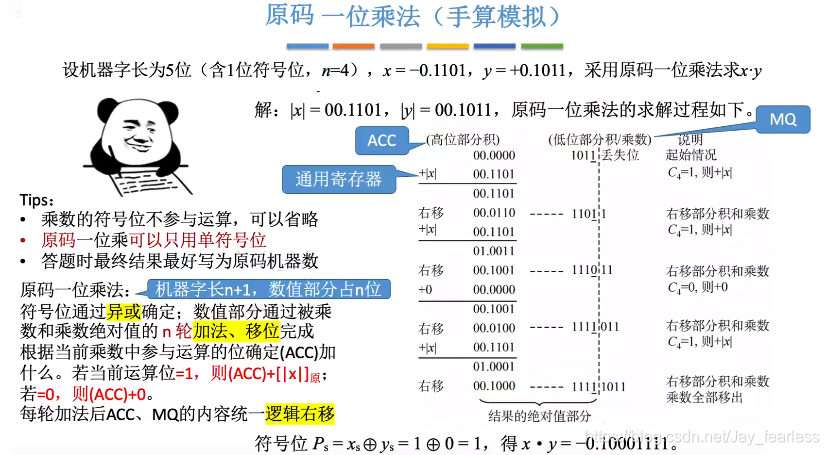
1.原码一位乘法
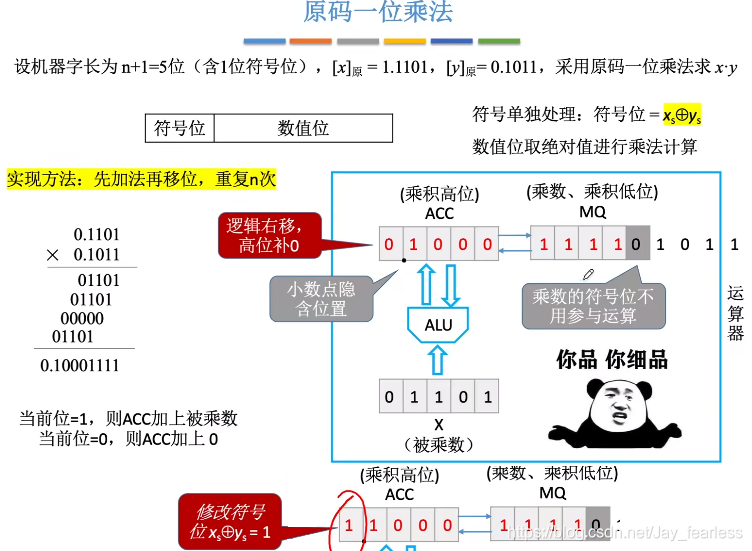
2.手动模拟
5.补码一位乘法
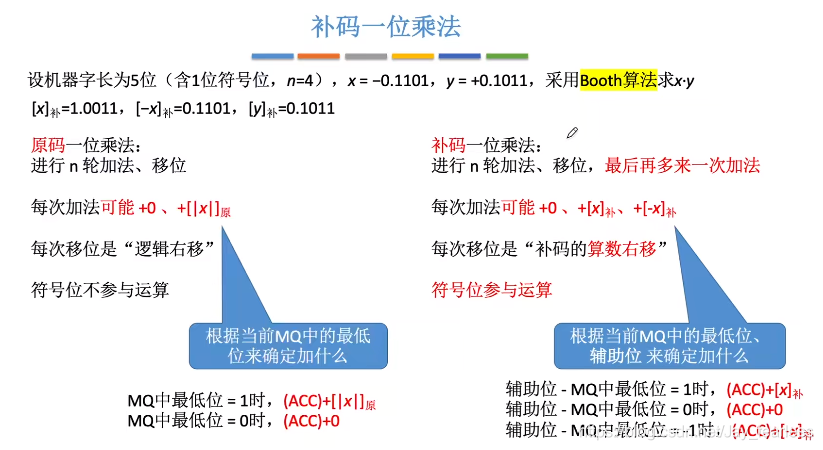
补码乘法运算要加上一个辅助位,初始为0
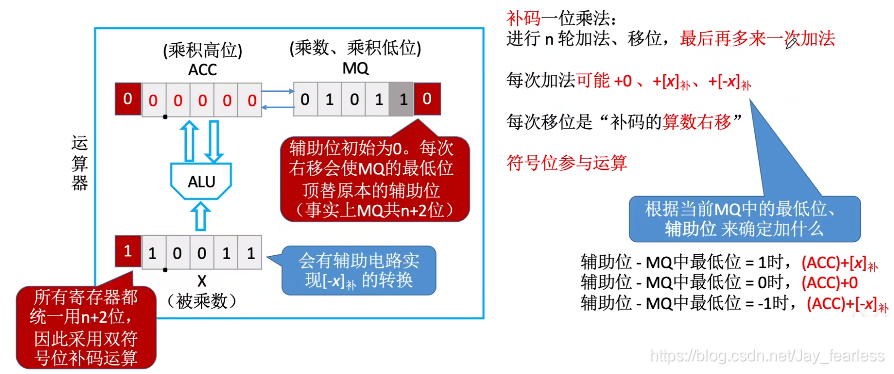
手动模拟
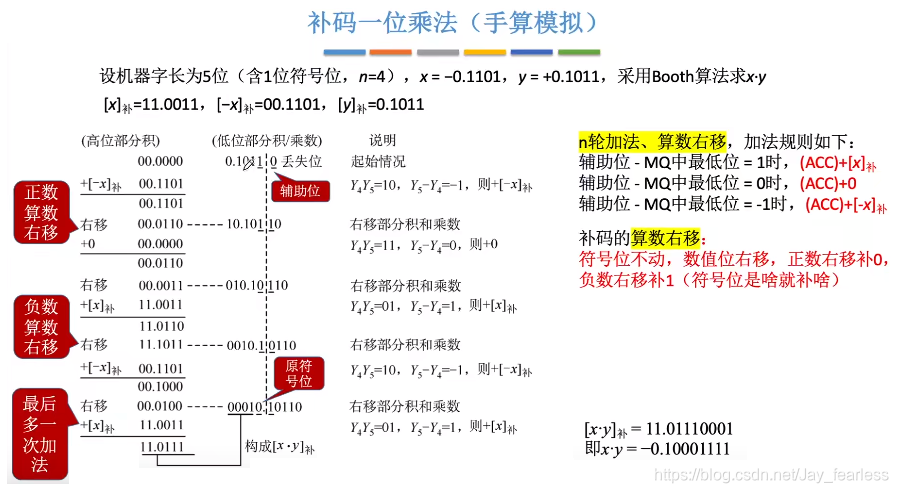





 本文详细讲解了定点数中的无符号数和有符号数(包括原码、反码、补码和移码),重点介绍了移位运算(逻辑右移与算术右移)及其在加减运算中的应用。通过实例说明了不同数制如何处理溢出和精度问题,以及原码乘法的一位乘法和补码乘法的手动模拟过程。
本文详细讲解了定点数中的无符号数和有符号数(包括原码、反码、补码和移码),重点介绍了移位运算(逻辑右移与算术右移)及其在加减运算中的应用。通过实例说明了不同数制如何处理溢出和精度问题,以及原码乘法的一位乘法和补码乘法的手动模拟过程。

















 2386
2386


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?









