本文将深入分析Mamba架构中交叉注意力机制的集成方法与技术实现。Mamba作为一种基于选择性状态空间模型的新型序列建模架构，在长序列处理方面展现出显著的计算效率优势。通过引入交叉注意力机制，Mamba能够有效处理多模态信息融合和条件生成任务。本文从理论基础、技术实现、性能分析和应用场景等维度，全面阐述了这一混合架构的技术特点和发展前景。

序列建模领域的发展历程中，注意力机制的出现标志着对长距离依赖关系处理能力的重大突破。Transformer架构凭借其自注意力机制在自然语言处理领域取得了革命性进展，但其二次方时间复杂度在处理超长序列时面临显著的计算和内存瓶颈。近年来，研究者们开始探索替代方案，其中Mamba架构作为一种基于选择性状态空间模型的新型序列建模方法，在保持线性时间复杂度的同时实现了对长序列的高效处理。

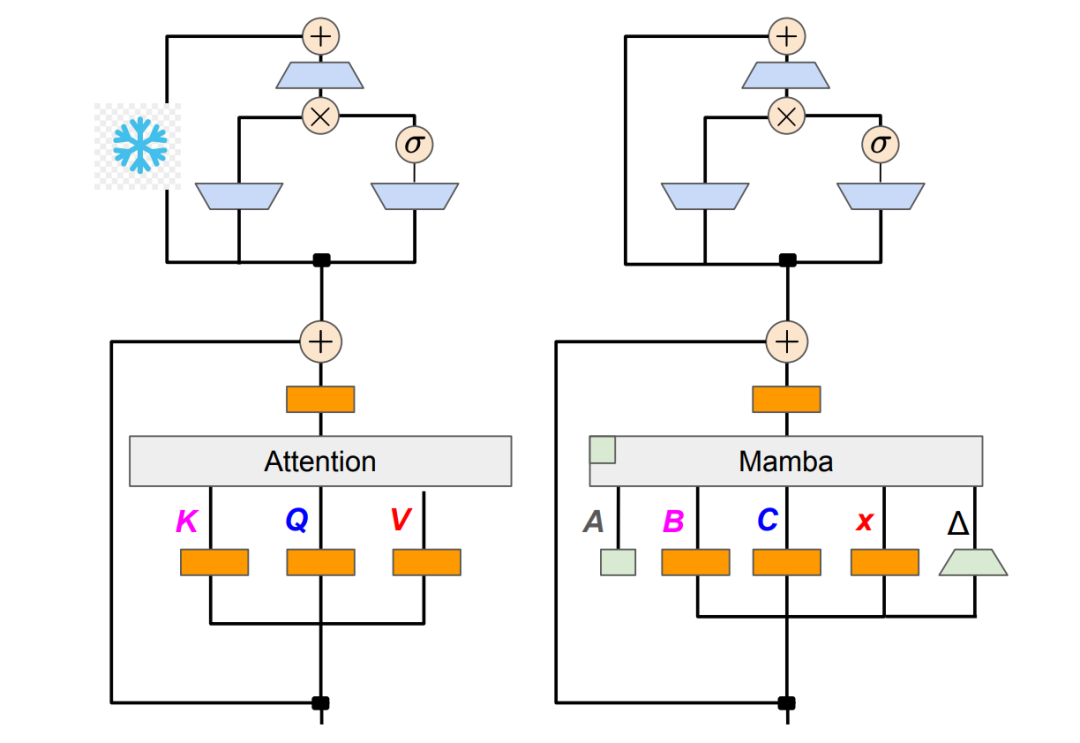
提升长序列建模效率：Mamba+交叉注意力架构完整指南_人工智能

然而原始的Mamba架构在多模态信息融合和条件生成任务中存在局限性，缺乏直接建模不同序列间交互关系的能力。为了克服这一限制，研究者们提出了在Mamba架构中集成交叉注意力机制的方法。这种混合架构结合了Mamba在长序列建模方面的效率优势和交叉注意力在跨序列信息整合方面的能力，为多模态应用和复杂条件生成任务提供了新的技术路径。

Mamba架构的理论基础与技术特点

状态空间模型的数学基础

Mamba架构的核心是选择性状态空间模型(Selective State Space Model)，其数学表示可以描述为连续时间动态系统。给定输入序列 x(t)，状态空间模型通过以下微分方程组进行建模：

提升长序列建模效率：Mamba+交叉注意力架构完整指南_人工智能_02

为了适应离散化的神经网络计算，连续时间系统需要通过零阶保持(Zero-Order Hold)方法进行离散化处理：

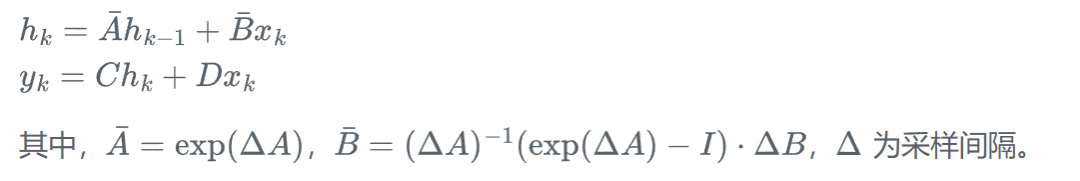
提升长序列建模效率：Mamba+交叉注意力架构完整指南_人工智能_03

选择性机制的工作原理

Mamba的核心创新在于引入了选择性机制，使得状态转移矩阵能够根据输入内容动态调整。具体而言，参数 B、C 和步长 \Delta 不再是固定值，而是通过输入依赖的函数计算得出：

提升长序列建模效率：Mamba+交叉注意力架构完整指南_mamba_04

这种选择性机制使得模型能够根据输入的重要性动态调整信息的保留和遗忘程度，从而在处理长序列时保持关键信息的同时过滤冗余内容。

计算复杂度分析

传统Transformer的自注意力机制具有 O(L^2d) 的时间复杂度和 O(L^2) 的空间复杂度，其中 L 为序列长度，d 为隐藏维度。相比之下，Mamba通过状态空间模型实现了 O(Ld) 的线性时间复杂度和 O(L) 的线性空间复杂度。这种复杂度优势在处理长序列时尤为显著，使得Mamba能够高效处理长度达到百万级别的序列。

具体的计算过程可以通过扫描算法(Scan Algorithm)高效实现：

defselective_scan(u, delta, A, B, C, D):
    """
    选择性扫描算法的核心实现
    Args:
        u: 输入序列 [batch, length, dim]
        delta: 步长参数 [batch, length, dim]
        A: 状态矩阵 [dim, state_size]
        B: 输入矩阵 [batch, length, state_size]
        C: 输出矩阵 [batch, length, state_size]
        D: 前馈项 [dim]
    """
    batch, length, dim=u.shape
    state_size=A.shape[1]
    
    # 离散化
    deltaA=torch.exp(delta.unsqueeze(-1) *A)  # [batch, length, dim, state_size]
    deltaB=delta.unsqueeze(-1) *B  # [batch, length, dim, state_size]
    
    # 初始化状态
    h=torch.zeros(batch, dim, state_size, device=u.device)
    outputs= []
    
    foriinrange(length):
        # 状态更新
        h=deltaA[:, i] *h+deltaB[:, i] *u[:, i].unsqueeze(-1)
        # 输出计算
        y=torch.einsum('bds,bds->bd', h, C[:, i]) +D*u[:, i]
        outputs.append(y)
    
     returntorch.stack(outputs, dim=1)
  • 1.
  • 2.
  • 3.
  • 4.
  • 5.
  • 6.
  • 7.
  • 8.
  • 9.
  • 10.
  • 11.
  • 12.
  • 13.
  • 14.
  • 15.
  • 16.
  • 17.
  • 18.
  • 19.
  • 20.
  • 21.
  • 22.
  • 23.
  • 24.
  • 25.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
与传统序列模型的对比分析

在序列建模领域，Mamba与传统方法存在显著差异。循环神经网络(RNN)和长短时记忆网络(LSTM)虽然具有线性时间复杂度，但由于其序列化计算特性难以并行化，且在处理长序列时存在梯度消失或爆炸问题。Transformer通过自注意力机制解决了并行化和长距离依赖建模问题，但其二次方复杂度限制了在长序列场景下的应用。

Mamba通过状态空间模型巧妙地结合了两者的优势：既保持了线性复杂度，又支持高效的并行计算。在训练阶段，Mamba可以通过卷积形式实现并行计算；在推理阶段，则可以通过递归形式实现常数内存的顺序生成。

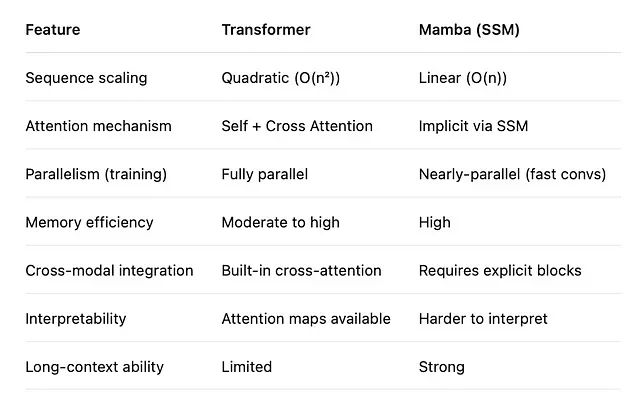
提升长序列建模效率：Mamba+交叉注意力架构完整指南_深度学习_05

交叉注意力机制的理论基础

交叉注意力的数学表达

交叉注意力机制允许一个序列(查询序列)对另一个序列(键值序列)进行注意力计算，其核心思想是建立不同信息源之间的交互关系。给定查询序列 Q \in \mathbb{R}^{L_q \times d}、键序列 K \in \mathbb{R}^{L_k \times d} 和值序列 V \in \mathbb{R}^{L_k \times d}，交叉注意力的计算过程如下：

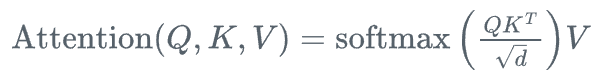
提升长序列建模效率：Mamba+交叉注意力架构完整指南_人工智能_06

其中，注意力权重矩阵 A \in \mathbb{R}^{L_q \times L_k} 表示查询序列中每个位置对键值序列中各个位置的关注程度。

多头交叉注意力

为了增强模型的表示能力，通常采用多头注意力机制，将查询、键、值分别投影到多个子空间进行并行计算：