你真的理解TreeMap吗?

1. TreeMap底层数据结构

TreeMap 是 Java 集合框架中基于 红黑树(Red‑Black Tree)实现的一个 有序映射。

它的数据结构非常简单，只使用了红黑树一种数据结构，不像HashMap和LinkedHashMap 那么复杂。

Entry内部类字段：

登录后复制

static final class Entry<K,V> implements Map.Entry<K,V> {
	K key;
	V value;
	Entry<K,V> left;       //左子节点
	Entry<K,V> right;      //右子节点
	Entry<K,V> parent;     //父节点
	boolean color = BLACK; //节点颜色：BLACK=true, RED=false
}

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.

key、value和color为当前对象的值，其它字段为构成红黑树所需的节点对象。数据结构如图：

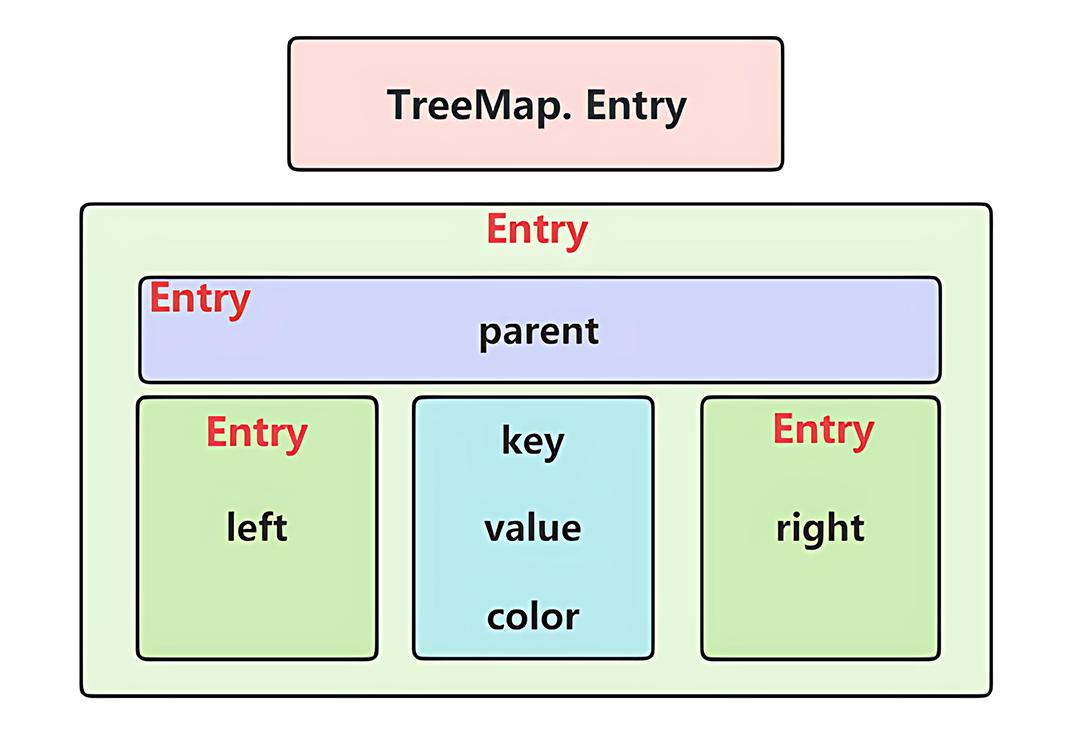
在Java中所有集合都是保存引用对象的引用，而非对象的值。TreeMap也是如此，在Entry对象中的Entry<K,V> left、Entry<K,V> right、Entry<K,V> parent 都只是保存着对象的引用(可以理解为地址指向)，而非具体的值。

Map集合的共性，只要知道key如何计算，便可知道value所在位置。在TreeMap中也是如此，最需要关注的是key在红黑树中的处理。

例如下图key在TreeMap中的存储：

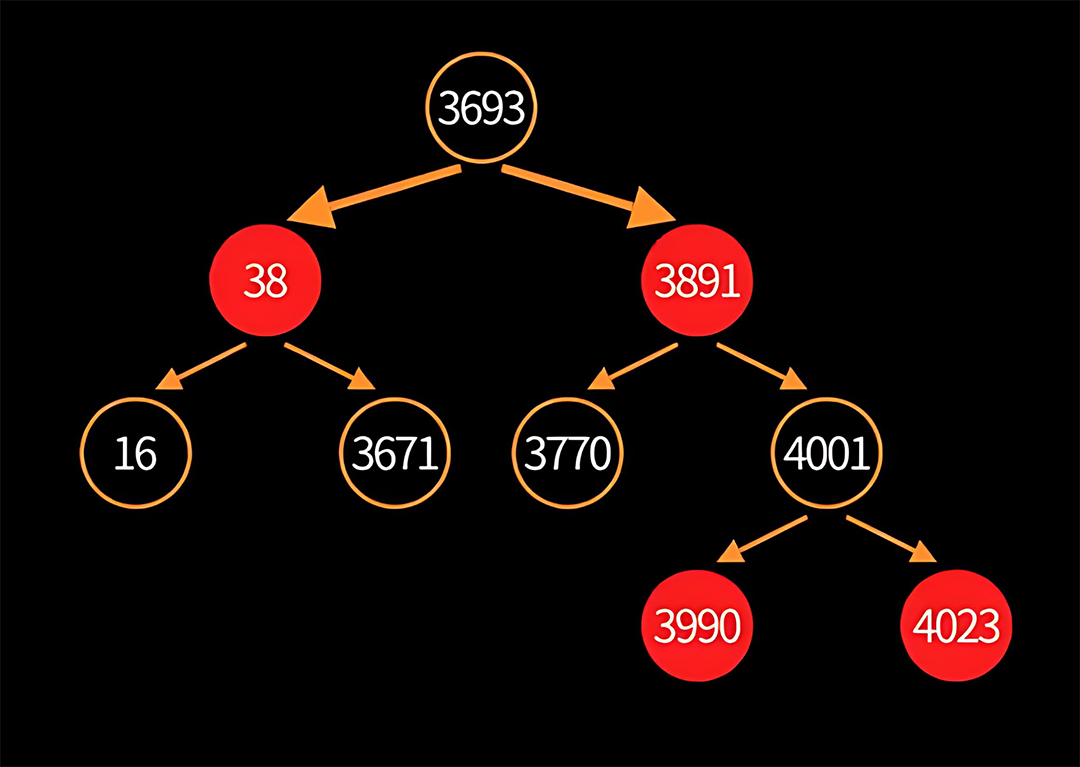
2. TreeMap 的特点

TreeMap 是 基于 红黑树(Red‑Black Tree)实现的一个 有序映射，特点是有序。这是由底层数据结构所带来的有序特性。

红黑树是一种自平衡二叉查找树，是一种有序的二叉树，按照左中右从小到大排序。

HashMap 同样也使用了红黑树，那是不是HashMap关于红黑树的那部分元素是有序的？没错，在HashMap中红黑树部分的元素是有序的，但是，它的有序性是根据key的hash值进行的排序，并且hash值在计算的过程中进行了扰动，就算没有扰动，hash值的有序对于使用者来说也没有意义，这种有序性仅用于维持红黑树。

而TreeMap集合的有序性是key值的有序，是根据key值进行的排序，这种有序性对于使用者来说才有实际性的价值。

哪么如何根据key值进行的排序呢？

2.1. TreeMap如何比较key值大小？

默认情况的比较，又称为自然顺序比较。TreeMap内部假定所有键类型都实现了 Comparable 接口，会直接调用key对象的中比较方法进行比较。

在插入、查找或删除时，会执行强制类型转换并调用：

登录后复制

((Comparable<? super K>) key).compareTo(existingKey)

• 1.

以确定 key 与树中节点 existingKey 的相对顺序(<0：key 更小；=0：相等；>0：key 更大)。

如果key对象未实现 Comparable，或尝试比较不同类型但不具备可比性的对象，将在运行时抛出 ClassCastException。

重点：

默认情况key值对象必须实现 Comparable 接口，并重写比较方法compareTo；

默认情况下 不允许 null 键，因为对 null 调用 compareTo 会导致 NullPointerException。

例如需要使用Person类作为键值key，实现Comparable接口：

登录后复制

public class Person implements Comparable<Person>{
    private final String name;
    private final int age;

    public Person(String name, int age) {
        this.name = name;
        this.age = age;
    }
    @Override
    public int compareTo(Person other) {
        int ageCmp = Integer.compare(other.age, this.age); // 降序
        if (ageCmp != 0) return ageCmp;
        return this.name.compareTo(other.name); // 升序
    }
}

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.

2.2. 如何自定义比较器(Comparator)？

如果key没有实现Comparable 接口，那么需要自定义比较器，并通过TreeMap的构造方法传入比较器 Comparator<? super K>，例如：

登录后复制

// 组合排序：先按 name 排序，再按 age 排序
Comparator<Person> cmp = Comparator
		.comparing(Person::getName)
		.thenComparingInt(Person::getAge);
Map<Person,Object> treeMap = new TreeMap<>(cmp);

• 1.
• 2.
• 3.
• 4.
• 5.

此时所有键的比较都由指定的自定义比较器方法决定。

比较键值key的大小分为两种：

• 自然顺序比较：键实现Comparable接口，调用compareTo。
• 自定义比较器：通过构造new TreeMap<>(Comparator<? super K> comparator)传入。

2.3. 为何选择红黑树？

在自平衡二叉查找树中，还有一种比较典型的AVL树，它相对于红黑树来说，平衡性的要求更严格，能够保持更高的平衡度。

AVL树在插入和删除时会进行更多的旋转操作，以确保任意节点左右子树的高度差不超过1。而红黑树允许一定程度的不平衡，以减少调整频率，提高插入删除的效率。

对比两者：

特性	AVL(强平衡)	红黑树(弱平衡)
平衡指标	每个节点左右子树高度差 ≤ 1	根到叶子的黑色节点数相同；红节点不能相连
树高上界	≈ 1.44 log₂ n	≤ 2 log₂ n
旋转开销	插入/删除可能多次旋转	最多 2 次旋转＋若干颜色翻转
查询效率	常数更小(更紧凑)	略逊于 AVL，但常数差距不大
更新开销	较高(为维护严格平衡)	较低(弱平衡条件更松)
应用场景	读多写少，对查询延迟要求极高	读写均衡，工业生产环境首选(如 Java、C++ STL)

数据结构的选择是一种取舍的抉择。 一种语言下的数据结构，一般都是以通用情况进行考量，而做出的选择。

红黑树相对于AVL树来说，牺牲了部分平衡性以换取插入和删除操作时少量的旋转操作，整体来说性能要优于AVL树。

关于AVL树和红黑树的选择：

• 当“查询性能”是唯一且最重要的考量时，AVL 的强平衡更有优势；
• 当需要在“查询”和“更新”之间做折中，且希望实现和维护都更简单时，红黑树的弱平衡更合适。

3. TreeMap在Java集合框架中扮演什么角色？

TreeMap与其他 Map 的对比

特性	HashMap	LinkedHashMap	TreeMap
底层结构	哈希表 + 链表/红黑树	哈希表 + 链表(维护插入/访问顺序)	红黑树
键排序	无序	保持插入顺序或访问顺序	按键的自然顺序或 Comparator 排序
时间复杂度	O(1)O(1) 平均	O(1)O(1) 平均	O(log⁡n)O(\log n)
允许 null 键	允许一个 null	允许一个 null	不允许 null 键
适用场景	追求最快的查找/插入	需要按插入或访问顺序迭代	需要按键排序、范围查询(subMap)等

TreeMap 填补了无序(HashMap)和插入/访问顺序(LinkedHashMap)之外的“键有序”需求。

应用场景

1. 需要范围查询：提供了对应的方法subMap、headMap、tailMap，例如 map.subMap(fromKey, toKey) 可以高效获取区间内所有条目。
2. 最小/最大元素快速访问：firstKey(), lastKey(), ceilingKey(), floorKey() 等导航方法。
3. 按排序顺序敏感的场景：中序遍历天然保证从小到大。
4. 需要按键排序的缓存或索引。

4. 核心API与功能

方法	描述	时间复杂度
put(K key, V v)	插入或更新键值对	O(log n)
get(Object key)	根据键查找值	O(log n)
remove(Object key)	删除节点	O(log n)
subMap(K fromKey, K toKey)	获取指定范围的视图	O(log n)
firstKey(), lastKey()	获取最小/最大键	O(log n)
ceilingKey(K key)	>=key的最小键	O(log n)

put, get, remove方法在此不演示，感受下有差异的方法。

• 如何通过subMap, headMap, tailMap等视图方法获取子区间？
• firstKey, lastKey, ceilingKey等导航方法的使用？

通过使用这些方法完成下面的案例。

4.1. 案例--商品订单量统计

假设我们要对一款电商商品的每小时下单量进行统计，并且在任意时刻都能快速获取：

• 过去 N 小时(如过去 3 小时)的订单总量；
• 某一时间段(如上午 10 点到下午 2 点)的小时级订单分布；
• 最近一次下单的时间(最晚的 key)。
• 等等。。。

这时，使用 TreeMap<LocalDateTime, Integer>，键按时间自然排序，就能轻松实现以上功能。

在此特别说明LocalDateTime为什么可以做键值key：

该类实现了Comparable接口可以做自然排序；

其次该类是final类不可被继承，同时该类的成员变量被final修饰，为不可变的变量。

实例源码如下：

登录后复制

import java.time.LocalDateTime;
import java.time.format.DateTimeFormatter;
import java.util.NavigableMap;
import java.util.TreeMap;

public class MinuteOrderStats {
    // 按分钟升序存储：key = 每分钟的起始时间(秒、纳秒都为0)，value = 该分钟的订单数量
    private final TreeMap<LocalDateTime, Integer> stats = new TreeMap<>();

    private final DateTimeFormatter fmt = DateTimeFormatter.ofPattern("yyyy-MM-dd HH:mm");

    /** 记录一次新订单，orderTime 精确到秒或更高 */
    public void recordOrder(LocalDateTime orderTime) {
        // 截断到分钟(保留年/月/日/时/分，秒和纳秒置零)
        LocalDateTime minute = orderTime.withSecond(0).withNano(0);
        // 累加同一分钟的新订单数，每次加1
        stats.merge(minute, 1, Integer::sum);
    }

    /** 统计从 now 向前 lookbackMinutes 分钟内的总订单量 */
    public int totalInPastMinutes(int lookbackMinutes) {
        LocalDateTime nowMin = LocalDateTime.now()
                .withSecond(0)
                .withNano(0);
        LocalDateTime from   = nowMin.minusMinutes(lookbackMinutes);
        // 包含 from 和 nowMin
        NavigableMap<LocalDateTime, Integer> sub = stats.subMap(from, true, nowMin, true);
        System.out.println("subMap [" + fmt.format(from) + ", " + fmt.format(nowMin) + "):");
        sub.forEach((k, v) -> System.out.println("  " + fmt.format(k) + " → " + v));
        return sub.values()
                .stream()
                .mapToInt(Integer::intValue)
                .sum();
    }

    /** 调试时打印所有分钟统计 */
    public void dumpAll() {
        stats.forEach((time, count) ->
                System.out.println(fmt.format(time) + " → " + count));
    }

    public void demo() {
        LocalDateTime now = LocalDateTime.now().withSecond(0).withNano(0);
        LocalDateTime start = now.minusMinutes(8);  // 8 分钟前
        LocalDateTime mid   = now.minusMinutes(5);  // 5 分钟前
        LocalDateTime end   = now.minusMinutes(2);  // 2 分钟前

        // 1. subMap(fromKey, toKey) — [from, to)
        System.out.println("\n—— 过去 5 分钟总订单量 ——");
        System.out.println("总订单量: "+totalInPastMinutes(5));

        System.out.println("\n—— 从8分钟前到2分钟前的分布 ——");
        NavigableMap<LocalDateTime, Integer> sub =stats.subMap(start, true, end, false);
        System.out.println("subMap [" + fmt.format(start) + ", " + fmt.format(end) + "):");
        sub.forEach((k, v) -> System.out.println("  " + fmt.format(k) + " → " + v));

        // 2. headMap(toKey) — (< toKey)
        System.out.println("\n—— 从头到5分钟前的分布 ——");
        NavigableMap<LocalDateTime, Integer> head = stats.headMap(mid, false);
        System.out.println("headMap (< " + fmt.format(mid) + "):");
        head.forEach((k, v) -> System.out.println("  " + fmt.format(k) + " → " + v));

        // 3. tailMap(fromKey) — [fromKey, ∞)
        System.out.println("\n—— 从5分钟前到末尾的分布 ——");
        NavigableMap<LocalDateTime, Integer> tail = stats.tailMap(mid, true);
        System.out.println("tailMap (≥ " + fmt.format(mid) + "):");
        tail.forEach((k, v) -> System.out.println("  " + fmt.format(k) + " → " + v));

        // 4. firstKey() — 最早的键
        System.out.println("\n—— 最早的键分布 ——");
        LocalDateTime first = stats.firstKey();
        System.out.println("firstKey(): " + fmt.format(first) + " → " + stats.get(first));

        // 5. lastKey() — 最晚的键
        System.out.println("\n—— 最晚的键分布 ——");
        LocalDateTime last = stats.lastKey();
        System.out.println("lastKey():  " + fmt.format(last) + " → " + stats.get(last));

        // 6. ceilingKey(key) — ≥ key 的最小键
        System.out.println("\n—— ≥ key 的最小键的键分布 ——");
        LocalDateTime query = now.minusMinutes(6).plusSeconds(30);
        LocalDateTime ceil = stats.ceilingKey(query);
        System.out.println("ceilingKey(" + fmt.format(query) + "): "
                + (ceil != null
                ? fmt.format(ceil) + " → " + stats.get(ceil)
                : "null"));
    }

    public static void main(String[] args) throws InterruptedException {
        MinuteOrderStats os = new MinuteOrderStats();
        LocalDateTime now = LocalDateTime.now();
        LocalDateTime hourAgo = now.minusMinutes(10);
        // 模拟插入：跨 3 分钟，每隔几秒记录一次
        for (int i = 0; i < 100; i++) {
            // 让时间分布在 now.minusMinutes(3) ~ now
            os.recordOrder(hourAgo.minusSeconds((3 * 60) - i * 7));
            Thread.sleep(5);
        }

        System.out.println("—— 全部分钟统计 ——");
        os.dumpAll();
        // 常见的集中操作
        os.demo();
    }
}

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.
• 30.
• 31.
• 32.
• 33.
• 34.
• 35.
• 36.
• 37.
• 38.
• 39.
• 40.
• 41.
• 42.
• 43.
• 44.
• 45.
• 46.
• 47.
• 48.
• 49.
• 50.
• 51.
• 52.
• 53.
• 54.
• 55.
• 56.
• 57.
• 58.
• 59.
• 60.
• 61.
• 62.
• 63.
• 64.
• 65.
• 66.
• 67.
• 68.
• 69.
• 70.
• 71.
• 72.
• 73.
• 74.
• 75.
• 76.
• 77.
• 78.
• 79.
• 80.
• 81.
• 82.
• 83.
• 84.
• 85.
• 86.
• 87.
• 88.
• 89.
• 90.
• 91.
• 92.
• 93.
• 94.
• 95.
• 96.
• 97.
• 98.
• 99.
• 100.
• 101.
• 102.
• 103.
• 104.
• 105.

案例测试结果

登录后复制

—— 全部分钟统计 ——
2025-06-29 23:16 → 2
2025-06-29 23:17 → 9
2025-06-29 23:18 → 8
2025-06-29 23:19 → 9
2025-06-29 23:20 → 9
2025-06-29 23:21 → 8
2025-06-29 23:22 → 9
2025-06-29 23:23 → 8
2025-06-29 23:24 → 9
2025-06-29 23:25 → 8
2025-06-29 23:26 → 9
2025-06-29 23:27 → 9
2025-06-29 23:28 → 3

—— 过去 5 分钟总订单量 ——
subMap [2025-06-29 23:24, 2025-06-29 23:29):
  2025-06-29 23:24 → 9
  2025-06-29 23:25 → 8
  2025-06-29 23:26 → 9
  2025-06-29 23:27 → 9
  2025-06-29 23:28 → 3
38

—— 从8分钟前到2分钟前的分布 ——
subMap [2025-06-29 23:21, 2025-06-29 23:27):
  2025-06-29 23:21 → 8
  2025-06-29 23:22 → 9
  2025-06-29 23:23 → 8
  2025-06-29 23:24 → 9
  2025-06-29 23:25 → 8
  2025-06-29 23:26 → 9

—— 从头到5分钟前的分布 ——
headMap (< 2025-06-29 23:24):
  2025-06-29 23:16 → 2
  2025-06-29 23:17 → 9
  2025-06-29 23:18 → 8
  2025-06-29 23:19 → 9
  2025-06-29 23:20 → 9
  2025-06-29 23:21 → 8
  2025-06-29 23:22 → 9
  2025-06-29 23:23 → 8

—— 从5分钟前到末尾的分布 ——
tailMap (≥ 2025-06-29 23:24):
  2025-06-29 23:24 → 9
  2025-06-29 23:25 → 8
  2025-06-29 23:26 → 9
  2025-06-29 23:27 → 9
  2025-06-29 23:28 → 3

—— 最早的键分布 ——
firstKey(): 2025-06-29 23:16 → 2

—— 最晚的键分布 ——
lastKey():  2025-06-29 23:28 → 3

—— ≥ key 的最小键的键分布 ——
ceilingKey(2025-06-29 23:23): 2025-06-29 23:24 → 9

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.
• 30.
• 31.
• 32.
• 33.
• 34.
• 35.
• 36.
• 37.
• 38.
• 39.
• 40.
• 41.
• 42.
• 43.
• 44.
• 45.
• 46.
• 47.
• 48.
• 49.
• 50.
• 51.
• 52.
• 53.
• 54.
• 55.
• 56.
• 57.
• 58.
• 59.
• 60.

4.2. 关于NavigableMap接口

TreeMap实现了NavigableMap接口，NavigableMap 接口是 Java 在 SortedMap 基础上扩展出来的一个接口，代表可导航的有序映射表。

它扩展了 SortedMap，支持更丰富的范围查询与方向遍历操作。

TreeMap实现了NavigableMap接口，使得TreeMap 具有更丰富的查询操作，已将方法汇总如下，可自行尝试。

方法总览

方法名	返回值类型	描述
lowerKey(K key)	K	严格小于给定键的最大键
floorKey(K key)	K	小于等于给定键的最大键
ceilingKey(K key)	K	大于等于给定键的最小键
higherKey(K key)	K	严格大于给定键的最小键
lowerEntry(K key)	Map.Entry<K,V>	严格小于给定键的最大条目
floorEntry(K key)	Map.Entry<K,V>	小于等于给定键的最大条目
ceilingEntry(K key)	Map.Entry<K,V>	大于等于给定键的最小条目
higherEntry(K key)	Map.Entry<K,V>	严格大于给定键的最小条目
subMap(fromKey, incl, toKey, incl)	NavigableMap	返回子视图，支持边界包含/排除控制
headMap(toKey, inclusive)	NavigableMap	返回 <= toKey 的子视图
tailMap(fromKey, inclusive)	NavigableMap	返回 >= fromKey 的子视图
descendingMap()	NavigableMap	返回一个键降序排列的视图
descendingKeySet()	NavigableSet	返回键集合的降序视图
pollFirstEntry()	Map.Entry<K,V>	弹出并移除最小键对应的条目
pollLastEntry()	Map.Entry<K,V>	弹出并移除最大键对应的条目

5. 源码阅读

TreeMap 源码的学习本质是红黑树数据结构的学习，关键源码为红黑树插入、删除和调平衡(染色和旋转)，重点关注TreeMap.put, TreeMap.remove, rotateLeft, rotateRight和fixAfterInsertion, fixAfterDeletion方法。

这些方法中最为主要的是：fixAfterInsertion 和 fixAfterDeletion方法。

5.1. 插入平衡：fixAfterInsertion

当你往红黑树里插入一个新节点时，通常分为两大步：

1.新节点染成红色(保证不破坏从根到叶子的黑色节点数一致性)。

2.如果它的父节点也是红色，就会违反“红色节点不能有红色子节点”这一性质，需进行修复：

• Case 1(叔叔节点也红)
  父、叔都染黑，祖父染红，指针上移到祖父，继续检查上层。
• Case 2(叔黑，且当前节点与父节点在同一侧)
  对父节点做一次旋转(左旋或右旋)，把自己变成父的位置，再归为 Case 3。
• Case 3(叔黑，且当前节点与父节点在“外侧”)
  将父染黑、祖父染红，然后对祖父做一次与父同方向的旋转。

fixAfterInsertion(Entry<K,V> x) 就是把这三个 Case 全部编码在一个while循环里，最终把根节点染黑，恢复所有红黑树性质。

可视化过程：

5.2. 删除平衡：fixAfterDeletion

删除节点更复杂，因为可能产生“双重黑”(double-black)问题。大致流程：

1.如果被删节点或被删替换节点是红色，则简单染黑，完事。

2.否则，当前“替代”节点(可能为 null 代表叶子)就相当于带了一个额外的黑色，需要通过一系列 Case：

• Case 1(兄弟节点是红色)
  将兄弟染黑、父染红，然后对父做一次旋转，使兄弟变成新的兄弟(变为黑色兄弟的场景)。
• Case 2(兄弟黑，且兄弟的两个子节点都黑)
  将兄弟染红，上移到父，继续在父节点处做平衡。
• Case 3(兄弟黑，兄弟的外侧子节点黑，内侧子节点红)
  将兄弟内侧子节点染黑、兄弟染红，然后对兄弟做一次旋转，转为 Case 4。
• Case 4(兄弟黑，兄弟的外侧子节点红)
  将兄弟染成父颜色、父染黑、兄弟外侧节点染黑，对父做一次旋转，结束。

fixAfterDeletion(Entry<K,V> x) 同样也是把以上 Case 都写一个while循环里，最终把根节点染黑。

删除根节点的可视化过程：

5. 总结

TreeMap底层数据结构、特点、与其他Map集合的差异，并提供一个简单案例感受TreeMap带来的高效处理。如果只关心 快速存取，且对顺序无要求，首选 HashMap； 如果需要按 插入或访问顺序 遍历，用 LinkedHashMap； 若需 按键排序、范围查询 或访问 最小/最大值，则应使用 TreeMap。