卡塔兰数和出栈顺序问题

文章目录

• 卡特蓝数

• 通项
• 递推

• 栈和catalan数

• 问题模型

• 使用树状图来枚举所有出栈可能

• 唯一性
• 枚举指定元素开头的出栈序列
• 判断非法出栈序列
• 不可能序列
• 根据出栈序列判断栈的最小容量
• 根据出栈序列换源入栈出栈操作序列
• 段序列的出栈可能枚举
• 综合应用

卡特蓝数

•  卡塔兰数 wikipedia

登录后复制

def factorial(n):

    if(n<0):
        # 对于非法输入(负数,我们抛出异常)
        raise ValueError(f"{n} must be a positive number!!")
    f=1
    while(n):
       f*=n
       n-=1
    return f

# print(factorial(5))
def catalan(n):
    # c=1/(n+1)*(factorial(2*n))/(factorial(n)**2)
    c=factorial(2*n)/(factorial(n+1)*factorial(n))
    return int(c)
# print(catalan(4))

# 打印前n个catalan数
def get_catalan_seq_tops(n):
    # l=[catalan(i) for i in range(1,n+1)]#如果从n=1开始计数
    print("n:catalan(n)")
    for i in range(0,n+1):#从n=0开始
        c=catalan(i)
        print(f"{i}:{c}")    
if __name__=="__main__":
    get_catalan_seq_tops(10)
#前十个: [1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796]
# PS D:\repos\PythonLearn>  py catalan.py
# n:catalan(n)
# 0:1
# 1:1
# 2:2
# 3:5
# 4:14
# 5:42
# 6:132
# 7:429
# 8:1430
# 9:4862
# 10:16796

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.
• 28.
• 29.
• 30.
• 31.
• 32.
• 33.
• 34.
• 35.
• 36.
• 37.
• 38.
• 39.
• 40.
• 41.

通项

递推

栈和catalan数

• 如果
  
  个不同元素{
  
  }进栈,出栈序列的个数为
  

• 若
  
  ,则
  
  必须比
  
  先入栈
• 第
  
  次入栈的元素只能是
  
• 然而不像入栈那么严格,虽然位序大的元素相对于位序小的元素后入栈,但是位序小的元素可以在位序大的元素入栈之前就出栈,这种条件下可以让先入栈的元素比后入栈的元素更早被弹出栈

• 简单讲,就是元素进栈后可以停留,也可以出栈,直到所有元素都出栈,求出栈的所有不同序列的数量或者枚举出具体的出栈序列
• 例如两个元素
  

• 操作序列:push(a1),pop(a1),push(a2),pop(a2),只要先入栈的元素在新元素入栈之前弹出,就会出现先入栈的元素比后入栈的元素更早弹出
• 这看似和栈的后进先出的特点不符,后进先出针对连续入栈和连续出栈的情况而言;
• 所以出栈的时候,位序大的元素一定比位序小的元素先出栈

• (允许栈非空的时候出栈,即使还有元素未进栈)
• 那么出栈的序列数(不同的排列数)为catalan(n)种

问题模型

• 用s表示push(入栈)
• 用x表示pop(出栈)
• 对n个元素的序列中的元素从左往右的顺序先后进栈,不要求连续入栈,栈非空时总是允许出栈,最终共执行n次入栈,n次出栈操作
• 如果设置2个操作计数器,分别统计push操作和pop操作执行的次数,那么push的数量始终大等于pop(或者说pop的次数始终不超过push的次数,否则出现空栈无元素可弹出的情况)
• 在上述条件下,找出所有的操作序列,显然序列开头是push操作,结尾是pop操作,push,pop都各有n次,序列长度为2n;

• 当序列中出现了
  
  次push,那么剩下的只有pop操作;
• 如果pop操作出现的次数达到push次数,并且还有元素没有入栈,那么下一步只能是push

• 显然,任何入栈出栈序列的第一个操作一定是把第一个元素入栈,但是后续的操作可能就多了;这是由于出栈操作可能发生在任何非空栈的情况下

使用树状图来枚举所有出栈可能

• 在上述问题模型的讨论中,我们可以借助树状图来枚举出所有可能
• 当序列长度不是很大的情况下,这是一个有效的手算方法
• 如果序列含有
  
  个元素的序列为,我们可以画出
  
  条分支,每条分支包含了
  
  个结点,分别对应于入栈和出栈操作
• 
  元素的序列对应的树有
  
  层,每层是一个入栈或者出栈操作,分别用s,x表示
• 树的分叉时,左侧为入栈,右侧为出栈;

• 结点右边的数字表示该操作是第几次(
  
  表示第
  
  次入栈,
  
  表示第
  
  次出栈)
• 设树中任意结点为
  
  ,则
  
  分支时要考察2个方面,

• 左分支入栈,如果入栈操作次数达到序列长度
  
  时,则之后无法在入栈,全部是出栈;否则可以入栈,并且观察该分支路径上最后一个入栈数字是几,新分支数字加1
• 有分支出栈,出栈前考察该路径上已入栈次数和已出栈次数是否相等,如果相等，则无法出栈(此时右分支缺失);若该路径上入栈次数多于出栈次数,那么可以继续出栈,并对出栈数字加1

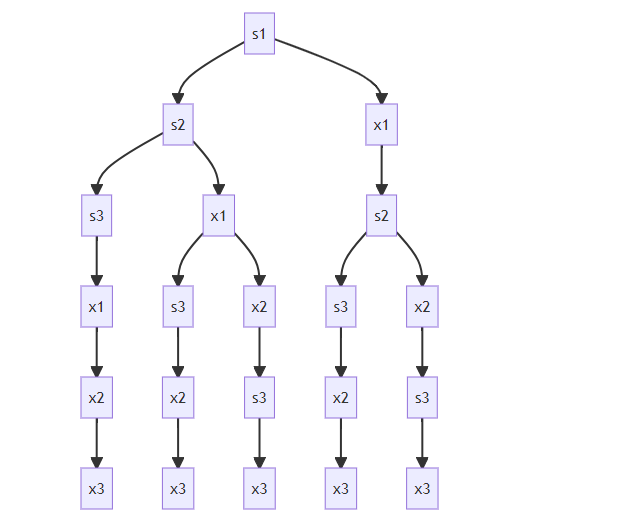
可以发现,各条路径的重点都是

;

根据树状图将出栈序列写出来:举个例子,比如路径序列:

其中由于第

次入栈的元素一定是

,我们可以依次观察出栈操作

,

前面离

最近的

型结点的下标就是第一个出栈元素,本例中是

,因此该路径第一个出栈的是

,将用掉的

划掉,

前面最近的

结点是

,说明第二个出栈的是

,最后序列剩下

,最后一次弹出的是

;

所以该例子中出栈序列为

唯一性

可以发现,上述枚举方法所有路径对应的序列都是互不相同的,每条路径对应唯一的出栈序列;反之,给定一个合法的出栈序列,可以找到对应的路径

枚举指定元素开头的出栈序列

上述的树状图枚举不仅仅可以用于全部枚举,还可以针对某一路径枚举

比如入栈序列

,长度达到5个,全部枚举出来会达到

=

种

如果我只想知道

开头的所有出栈序列,可以怎么做?

如果是

开头的序列,说明

出栈前

连续入栈,然后出栈

;对应的操作序列为ssssx

按照这个操作序列:将树状图补全,可以得到4条路径,将他们转换为出栈序列:

• decba
• dceba
• dcbea
• dcbae

判断非法出栈序列

比起枚举出所有可能的出栈序列,判断一个给定的序列是否合法相对容易

非法(不可能出现的)出栈序列原因可能是想要将非栈顶元素出栈

例如入栈顺序

那么出栈顺序

是非法的

分析:第一个出栈的是

,则说明

最开始依次入栈,然后弹出c,接着试图弹出a,然而a不是栈顶元素,因此该操作非法

有时给定的出栈信息不一定是整个序列完整给出,可能给出部分信息,比如第2,4个出栈元素,其余两出栈信息不给出,这种情况下直接判断不方便,考虑将出栈信息通过枚举所有可能性补全序列,然后逐个判断是否存在合法序列,如果所有序列都非法,那么原不完整序列也是不可能的;这种做法对于短序列比较有效,如果给出的序列中有较多不定数,枚举量就比较大了

不可能序列

• 弹出非栈顶元素是不可能序列的一个基本特征,但是直接拿来判断并不够方便
• 可以验证,当
  
  比
  
  先出栈,那么
  
  和
  
  在出栈序列中一定是相邻的,否则就是非法的

• 因为
  
  出栈后可以断定
  
  此前已经入栈;而
  
  若要在
  
  后出栈,那么只能是
  
  出栈后,
  
  立即出栈,因为
  
  之间没有别的元素可以直接出栈,也没有更大位序的元素可以入栈后出栈,如果要隔一个元素出栈,那么就得将
  
  之前的元素出栈,这些都是非栈顶元素,是非法的
• 因此,若入栈序列为
  
  ,那么出栈序列中,若3在4之后出栈,那么4,3在序列中紧邻

• 然而,若1在2之后出栈,那么2,1不一定是紧邻的,因为2,1不是最后两个入栈的元素

根据出栈序列判断栈的最小容量

• 根据出栈序列还原出入栈/出栈操作序列
• 设置一个计数器,入栈+1,出栈-1;将计数器在整个过程中出现的最大值作为栈的最小容量
• 例如入栈序列为
  
  的某个出栈序列为
  
  ,那么

• 还原出进栈(s)/出栈(x)操作序列,并且在每个操作下记录当前栈中元素数量

s	s	x	s	s	x	x	s	s	x	x	x	s	x
1	2	1	2	3	2	1	2	3	2	1	0	1	0

可见,过程中最大最大元素数量为3,所以栈的最小容量为3

根据出栈序列换源入栈出栈操作序列

该操作也相对简单,从第一个出栈元素开始,如果是入栈序列中的第

个元素,说明前

个元素已经入栈,类似地可将整个入栈/出栈序列的操作还原出来

段序列的出栈可能枚举

• 1个元素({1}),显然只有一种出栈序列
• 2个元素({1,2}),则出栈序列可能有如下2种

• 12

• 出入栈操作序列:(sxsx)

• 21

• 出入栈操作序列(ssxx)

• 3个元素({1,2,3})先后进栈(中途允许出栈),则出栈序列可能有如下5种

• 123 sxsxsx
• 132 sxssxx
• 213 ssxxsx
• 231 ssxsxx
• 321 sssxxx

• 4个元素({1,2,3,4})先后进栈(中途允许出栈),则出栈序列可能有如下14种

• 1234
• 1243
• 1324
• 1342
• 1432
• 2134
• 2143
• 2314
• 2341
• 2431
• 3214
• 3241
• 3421
• 4321

综合应用

已知第

出栈元素,求第

个出栈元素可能是多少

例如,入栈序列为

,出栈序列记为

;若

,则

可能取值有多少中情况?

这个问题不向具体序列那样直白,根据经验和栈的特点判定

若

,让

即可,所以

有可能

若

,令

即可,所以

有可能

而3已经被

占领(早就弹出了),因此

显然可以取

(共

个取值);只要在3出栈后,每次入栈序列

的元素后立刻出栈即可做到

;

综上

有

中取值(只有3不可能取到)

方法2:

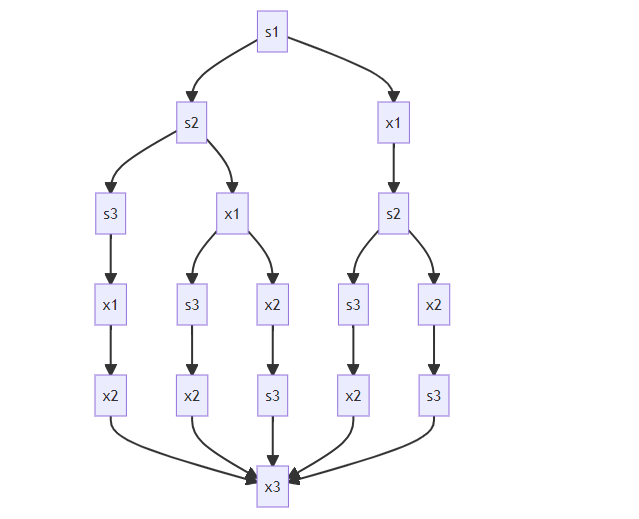
使用树状图判断(入栈为s,出栈为x)

第2个出栈元素是

,那么 s3->x2,在 s3及其上面部分 s1->s2->s3,其中有一个位置是 x1,可能是 s1->x1->s2->s3或 s1->s2->x1->x3分别对应于

和

的情况

最后,x2结点下开始分支,左侧可以从

一直到

,这些结点右侧分支都是 x3分别对应于

的情况

综上

共

个可能