如何处理回归模型中的异方差性和自相关性问题?(python)

1 什么是基本假设与违背基本假设？

在回归模型中，一般假设误差的均值为0，且不同误差项之间的方差相等、独立或者不相关：

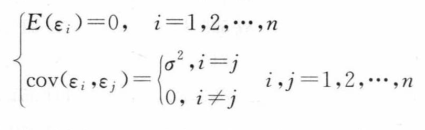
但实际建模过程中，误差项的方差可能不等，即异方差性：

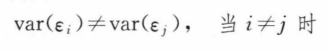
或者误差项间的协方差不为0，即存在自相关性：

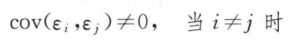
这里的自相关不是指两个或两个以上的变量之间的相关关系，而是指一个变量前后期数值之间的相关关系。

2 异方差产生的原因？

在实际建模时，经常会出现某一因素或某些因素随着解释变量观测值的变化而对被解释变量产生不同的影响，导致随机项产生不同的方差。比如90年的房价方差与20年的房价方差，就存在巨大的差异。

3 异方差会带来哪些问题？

当数据存在异方差时，就不能用PLS，因为PLS会高估回归系数，导致不显著的系数变为显著。具体问题有：

• 参数估计值虽是无偏的，但不是最小方差线性无偏估计
• 参数的显著性检验失效
• 回归方程的应用效果极不理想

4 如何判定数据存在异方差？

1)残差图分析法

以残差为纵坐标，其他变量为横坐标画散点图。常用横坐标：y的拟合值、x、观测时间或序号。

根据残差图如何判定：

• 当回归模型满足所有假定时，残差图上的n个点的散布应是随机的，无规律。
• 如果回归模型存在异方差，残差图上的点的散布会呈现出一定的趋势。比如残差随x值得增大而增大或减小而减小，具有明显的规律。

登录后复制代码解读

#建模
result = smf.ols('y~x',data=df).fit() 
para = result.params
#打印模型的参数
print(result.summary())
 
#计算残差
eres = result.resid
#print(eres)
 
#残差图
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(eres, 'o', label='resid')
ax.plot([0, 53], [0, 0], c='black', linestyle='-',alpha = 0.4)

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.

2)等级相关系数法

等级相关系数法又叫斯皮尔曼检验。其检验通常有三步：

注意：斯皮尔曼相关系数可以更准确地反映非线性相关的情况，可以如实反映具有单调递增或单调递减趋势的变量间的相关性，而pearson简单相关系数不能反映非线性相关的情况，只适宜衡量具有直线趋势的变量间的相关性。

登录后复制代码解读

#残差取绝对值
abse = abs(eres)
 
#spearman相关系数检验
cortest1 = scipy.stats.spearmanr(df['x'],abse)
print(cortest1)

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.

5 异方差数据如何建模？

思路：对原来的模型进行变换，使变换后的模型满足同方差性假设，然后进行模型参数的估计，即可得到理想的回归模型，具体方法有：

• 加权最小二乘法
• BOX-COX变换法
• 方差稳定性变换法等

1)一元加权最小二乘

思路：给不同的方差分配不同的权重，即加入一个适当的权数，使方差大的变小，方差小的变大，以调整各项方差在平方和中的作用。其离差平方和为：

在使用加权最小二乘法时，为了消除异方差性的影响，观测值的权数应该是观测值误差项方差的倒数：

登录后复制代码解读

#加权最小二乘法
 
loglik_list = []
result_list = []
 
#遍历取不同的值(即权重)
for i in np.arange(-2, 4, 0.5):  
    w = df['x']**(-i)
    resultw = smf.wls('y~x',data=df,weights=w).fit()
    loglik_list.append(resultw.llf)
    result_list.append(resultw.summary())
 
logresult = pd.Series(loglik_list)
#打印出每种情况下的对数极大似然统计量的值，值越大越好，最大的值对应的i值就是变量的权重
print(logresult)
print(result_list[logresult.idxmax()])
 
#确定最优的权重，然后从新建模
w = df['x']**(最优权重)
resultw = smf.wls('y~x1+x2',data=df,weights=w).fit()

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.

举个例子，如下图就是打印出来的部分结果：

这里打印出-2，-1.5，-1，-0.5，0，0.5，1，1.5，2，2.5，3，3.5，4这几个i字对应的对数极大似然估计值，比较得到第8个数最大，对应的i值为2，所以就确定权重为2。

2)多元加权最小二乘

多元回归中，变量太多，只需要对一个变量进行加权就可以。计算出每个变量与残差的等级相关系数，选取最大的等级系数进行最小二乘法的加权确定权重就可以了，在权重确定这一步的方法和一元的方法相同。

登录后复制代码解读

#等级系数计算和spearman相关系数检验，有几个因变量，
#我们就计算几次，然后比较选最大的等级相关系数的变量进行权重的确定
cortest1 = scipy.stats.spearmanr(df['x1'],abse)
print(cortest1)
 
cortest1 = scipy.stats.spearmanr(df['x2'],abse)
print(cortest1)
 
#这里我们假设x1的等级相关系数最大，故选取x1进行权重的确定
#加权最小二乘法
 
loglik_list = []
result_list = []
 
for i in np.arange(-2, 4, 0.5):
    
    w = df['x']**(-i)
    resultw = smf.wls('y~x',data=df,weights=w).fit()
    loglik_list.append(resultw.llf)
    result_list.append(resultw.summary())
 
logresult = pd.Series(loglik_list)
print(logresult)
print(result_list[logresult.idxmax()])
 
w = df['x']**(最优的权重)
resultw = smf.wls('y~x',data=df,weights=w).fit()

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.
• 10.
• 11.
• 12.
• 13.
• 14.
• 15.
• 16.
• 17.
• 18.
• 19.
• 20.
• 21.
• 22.
• 23.
• 24.
• 25.
• 26.
• 27.

6 自相关性产生的原因？

自相关产生的原因有：

• 遗漏关键变量时会产生序列的自相关性。若遗漏的变量在时间顺序上的影响是正相关的，则方程的误差项会有明显的正相关性，因为误差包含了遗漏变量的影响。
• 经济变量的滞后性会给序列带来自相关性。
• 采用错误的回归函数形式可能引起自相关性。
• 蛛网现象可能带来序列的自相关性。蛛网现象是微观经济学中研究商品市场运行规律所用的一个名词，表示某种商品的供给量因受前一期价格影响而表现出来的某种规律性，呈蛛网状收敛或发散于供需的均衡点。
• 因对数据加工整理而导致误差项之间产生自相关性。

7 自相关性会带来哪些问题？

8 如何判定数据存在自相关性？

1)图示检验法

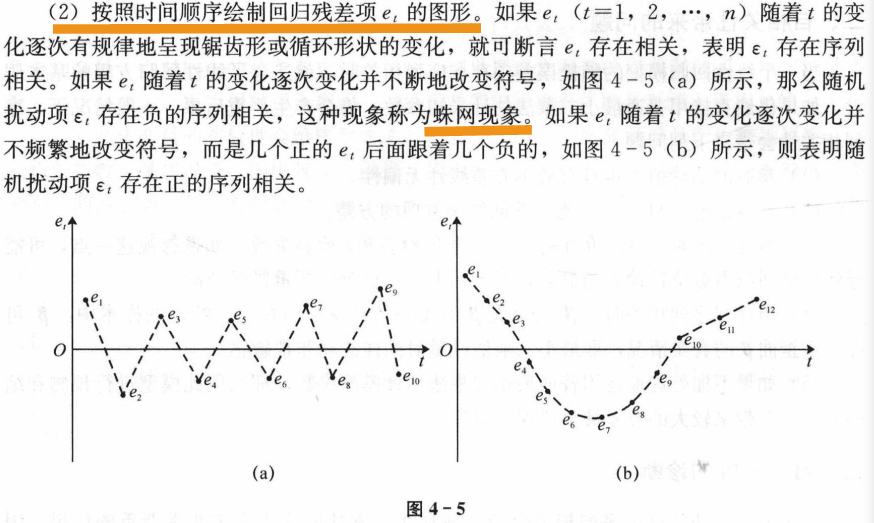
2)自相关系数法

.

3)DW 检验

DW检验是杜宾和沃特森于1951年提出的适用于小样本的一种检验方法。只能用于检验随机扰动项具有一阶自回归形式的序列相关问题。

令：

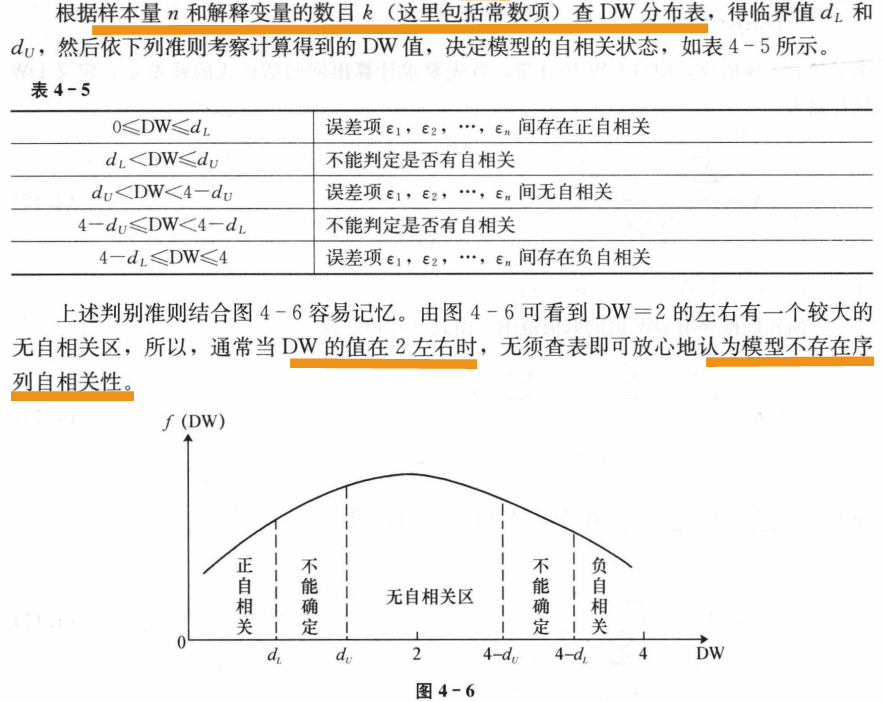
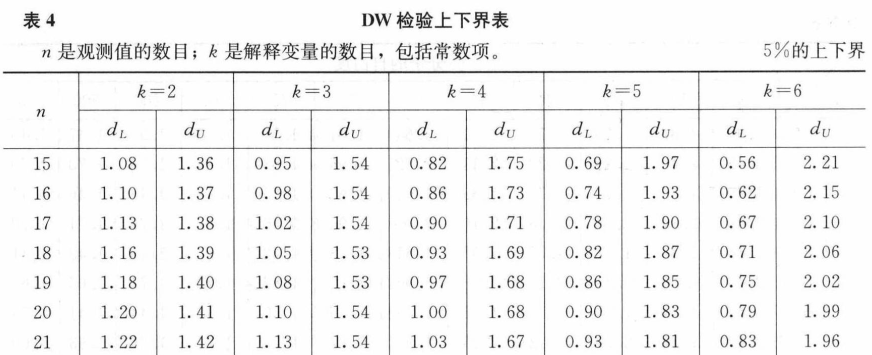
DW缺点：

• 有两个不能确定的区域，一旦DW值落在这两个区域，就无法判断，这时，只能增大样本量或采取其他方法。
• DW统计量的上下界表要求n>15，若样本过少，难以利用残差判断自相关性。
• 不适合高阶序列相关的随机项。

登录后复制代码解读

#建模
result = smf.ols('y~x',data = df)
#DW检验
DW = sm.stats.durbin_watson(result.resid)
rho = 1-0.5*DW
print('DW值：',DW)
print('ρ的值：',rho)

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.

9 自相关性如何处理？

选用其他形式的模型或增加变量是无法消除序列相关性的，可以采用迭代法、差分法等。

1)迭代法

式中的ρ是未知的，可通过DW检验估算。当误差项u通过DW检验时，自相关消除，迭代终止。

登录后复制代码解读

df = pd.read_csv("data.csv")
 
#迭代法解决自相关性
dfnew = (df-rho*df.shift(1)).dropna()  #迭代公式
 
resultnew = smf.ols('y~x',data=dfnew).fit() #重新建模
 
print(resultnew.summary()) # 打印出模型的结果

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.

代码中的shift(1)是数据表中从第几行开始进行迭代，一般格式为shift(n)，这里的n是数据从第几条开始迭代，注意Python是从0开始计数的。dropna() 函数主要用于过滤去除缺失数据的列或者行，因为我们是从第二条数据开始迭代的，第一条数据就会变为空，就直接赋予空值，不再计算。

2)差分法

用增量数据代替原来的样本数据，将原来的回归模型变为差分形式的模型。一阶差分适用于较高程度的一阶自相关。

迭代法和差分的区别：

登录后复制代码解读

df = pd.read_csv("data.csv")
#差分法解决自相关性
dfnew2 = (df-df.shift(1)).dropna()
 
print(dfnew2)
 
resultnew2 = smf.ols('y~x-1',data=dfnew2).fit() 
 
print(resultnew2.summary())

• 1.
• 2.
• 3.
• 4.
• 5.
• 6.
• 7.
• 8.
• 9.

注意差分法的使用，它是不需要截距项的。