AI：深度学习之循环神经网络（RNN）

🔄 从零入门循环神经网络（RNN）：原理详解+代码实战+未来展望 🚀

摘要：在人工智能蓬勃发展的当下，循环神经网络（Recurrent Neural Network, RNN）是处理序列数据的“记忆大师”🧠，正发挥着举足轻重的作用。从自然语言处理中的文本生成、机器翻译，到语音识别、时间序列预测等领域，RNN 都展现出了强大的能力，为解决复杂的序列相关问题提供了有效的方案。本文用比喻+代码+实战，带你从菜鸟到进阶！（建议收藏⭐）

---

一、RNN为什么而生？——当普通神经网络遇上“健忘症”

1.1 传统神经网络的短板：金鱼的7秒记忆 🐟

想象一下，你正在读一本小说📖。如果每次只看一页就忘记前面的内容，你永远无法理解故事的发展。传统的神经网络（如CNN）就像这样：每个输入独立处理，没有记忆能力。比如预测股票价格时，如果只看今天的K线，忽略历史数据，结果必然离谱！

举个栗子🌰：
输入句子“我想吃北京烤鸭”，传统神经网络会孤立分析每个词：“北京”→“首都”，“烤鸭”→“食物”，但无法联系上下文理解整句话的意图。而RNN会记住前面的“吃”，推测后续大概率是食物名。

1.2 RNN的杀手锏：自带“记忆笔记本”📒

RNN通过隐藏状态（Hidden State） 保存历史信息，形成循环结构。就像写日记时，每次记录新内容都会回顾之前的条目。这种设计让RNN能处理：

• 文本（如机器翻译）
• 语音（如微信语音转文字）
• 时间序列（如股票预测）

---

二、解剖RNN：结构原理全解析 🔍

2.1 RNN的“三件套”——输入层、隐藏层、输出层

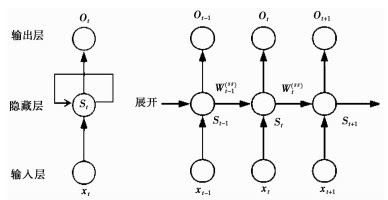
• 输入层：接收当前时间步的数据（如t时刻的单词）
• 隐藏层：核心记忆单元，计算公式：
  hₜ = σ(Wᵢ·xₜ + Wₕ·hₜ₋₁ + b)
  （σ是激活函数，W是权重，b是偏置）
• 输出层：生成预测结果（如下一个单词的概率分布）

2.2 举个栗子🌰：用RNN预测股票走势 📈

假设我们要预测某股票第4天的价格，输入是前3天的收盘价：

时间步1（t=1）：输入10 → 隐藏状态h₁=0.5  
时间步2（t=2）：输入20 → h₂=σ(20*Wᵢ + 0.5*Wₕ + b)  
时间步3（t=3）：输入30 → h₃=σ(30*Wᵢ + h₂*Wₕ + b)  
输出层：用h₃预测第4天价格

关键点：每个时间步共享同一组参数（Wᵢ, Wₕ），大大减少计算量！

---

三、RNN的进化之路：从基础款到变形金刚 🤖

3.1 简单循环神经网络（Simple RNN）的痛点：长序列失忆症 😵

当序列过长时，梯度消失/爆炸问题会导致模型“忘记”早期信息。比如分析一篇长论文时，可能只记得最后几段。

Simple RNN 是循环神经网络的基础形式，它的结构较为简洁 。在 Simple RNN 中，隐藏层在每个时间步接收当前输入和上一时刻隐藏层的输出 。以文本处理为例，当输入一个单词序列时，每个单词对应的向量依次进入网络 。假设我们有一个单词序列 “我 喜欢 深度学习” ，在第一个时间步，单词 “我” 对应的向量$x_1$与初始隐藏状态$h_0$（通常初始化为零向量）共同进入隐藏层 。隐藏层通过公式$h_1=\sigma (W_{hh}{h}_0+W_{xh}{x}_1+b_h)$计算得到当前隐藏状态$h_1$，其中$W_{hh}$和$W_{xh}$是权重矩阵，$b_h$是偏置，$\sigma$是激活函数（如 tanh） 。这个计算过程就像是一个简单的信息融合过程，将当前输入的单词信息和之前的状态信息整合在一起 。接着，第二个时间步，单词 “喜欢” 的向量$x_2$与$h_1$进入隐藏层，计算得到$h_2$，以此类推 。在最后一个时间步，隐藏状态$h_n$可以用于预测输出，比如预测下一个单词 。

然而，Simple RNN 在处理长序列时存在明显的局限性 。随着序列长度的增加，它会面临梯度消失或梯度爆炸问题 。从反向传播算法（BPTT）的角度来看，在计算梯度时，由于权重矩阵在时间步上的连乘操作 。假设激活函数为线性函数（为了简化分析，实际中激活函数会使情况更复杂但原理类似），在反向传播计算梯度时，会出现形如$\frac{\partial L}{\partial W}={\prod }_{t=1}^{T}W$（$L$为损失函数，$W$为权重矩阵，$T$为序列长度）的连乘项 。当$|W|<1$时，随着$T$的增大，连乘结果趋近于 0，导致梯度消失，模型难以学习到长距离的依赖关系，就好像在一个很长的故事中，Simple RNN 会逐渐忘记开头的信息 ；当$|W|>1$时，连乘结果会迅速增大，引发梯度爆炸，使得模型训练不稳定，参数更新过大导致无法收敛 。这就限制了 Simple RNN 在处理长文本、长时间序列等需要捕捉长期依赖关系数据时的表现 。

3.2 进阶版RNN：长短期记忆网络（Long Short-Term Memory，LSTM） 🚀

为了解决 Simple RNN 的长期依赖问题而被提出，它在结构上引入了门控机制，就像一个智能的信息过滤器，能够更好地处理长期依赖关系 。

LSTM：三重门控的保险箱 🔑

• 遗忘门：决定丢弃哪些旧记忆
• 输入门：筛选新信息存入记忆
• 输出门：控制当前时间步的输出

代码片段（TensorFlow实现）：

# 定义LSTM层（来自网页10）
lstm_cell = tf.keras.layers.LSTM(units=64)
outputs = lstm_cell(inputs)

具体计算过程如下

假设在时间步$t$，输入为$x_t$，上一时刻隐藏状态为