AI：支持向量机（SVM）

支持向量机（SVM）理论基础详解：从零开始的完全指南

一、SVM的核心思想：直观理解

1.1 什么是分类问题？

想象你在玩一个游戏：桌上有红色和蓝色的球，你需要画一条线把它们分开。这条线就是分类边界。SVM的目标是找到一条最优分界线，使得这条线到最近的红色球和蓝色球的距离（间隔）最大。

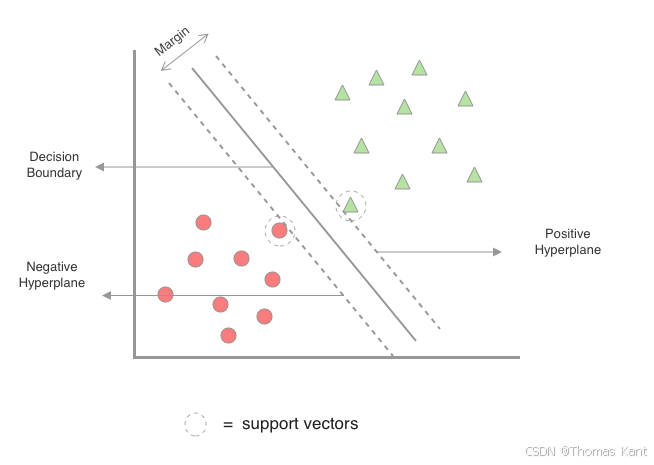
1. 二维坐标系中红色点和绿色三角形分别代表两类样本
2. 黑色实线为最优分类超平面（决策边界）
3. 两条虚线表示分类间隔边界（间隔带）
4. 被圆圈标注的样本点为支持向量
5. 箭头标注间隔距离（Margin Width）

1.2 关键术语解释

• 超平面：在N维空间中的N-1维分界平面（二维是直线，三维是平面）
• 间隔（Margin）：分界线到最近数据点的距离
• 支持向量：离分界线最近的样本点（图中红色和蓝色的边缘点）

类比理解：
把SVM想象成建一座最宽的"隔离带"，支持向量就是隔离带边缘的"护栏"，决定了隔离带的宽度和位置。

---

二、数学原理：从几何到优化

2.1 几何间隔：如何衡量分类质量？

对于任意数据点 $(x_i,y_i)$（$y_i=\pm 1$ 表示类别），到超平面 $w^{T}x+b=0$ 的距离公式为：
$$\text{几何间隔}=\frac{|w^T{x}_i+b|}{\Vert w\Vert }$$

为什么重要？
几何间隔越大，分类的置信度越高。SVM的目标是最大化所有样本的最小几何间隔。

2.2 线性可分SVM的优化问题

将最大化间隔转化为数学优化问题：
$$\begin{array}{rl}\underset{w,b}{\max }& \underset{i}{\min }\frac{y_i(w^T{x}_i+b)}{\Vert w\Vert }\\ \text{s.t.}& y_i(w^T{x}_i+b)\ge 1(\forall i)\end{array}$$

等价转换：
通过缩放技巧，简化为更易求解的凸二次规划问题：
$$\begin{array}{rl}\underset{w,b}{\min }& \frac{1}{2}\Vert w{\Vert }^2\\ \text{s.t.}& y_i\end{array}$$