AI：机器学习模型-逻辑回归_逻辑回归 ai算法-优快云博客

机器学习-逻辑回归：从原理到实战详解

一、为什么需要逻辑回归？

在这里插入图片描述

1.1 分类问题的离散预测需求

在现实世界的众多领域中，我们常常面临各种各样的分类任务。例如在医疗领域，医生需要根据患者的各项检查指标，如年龄、症状、检查报告数据等，来判断患者是否患有某种疾病；在金融领域，银行需要依据客户的信用记录、收入水平、负债情况等信息，评估客户是否具有违约风险，以此决定是否批准贷款申请；在电商领域，平台需要根据用户的浏览历史、购买行为、收藏偏好等数据，预测用户是否会购买某件商品，从而进行精准营销。这些问题的共同特点是，我们需要根据一系列的输入特征，对目标进行分类，而目标的取值是离散的类别，不是连续的数值。传统的线性回归模型主要用于预测连续值，如房价、气温等，无法直接处理这种离散的分类问题。因此，我们需要一种专门适用于分类任务的模型，逻辑回归应运而生。它能够通过学习输入特征与输出类别之间的关系，预测二元结果（0 或 1，真或假，是或否），满足了分类问题的离散预测需求。

1.2 逻辑回归的独特优势

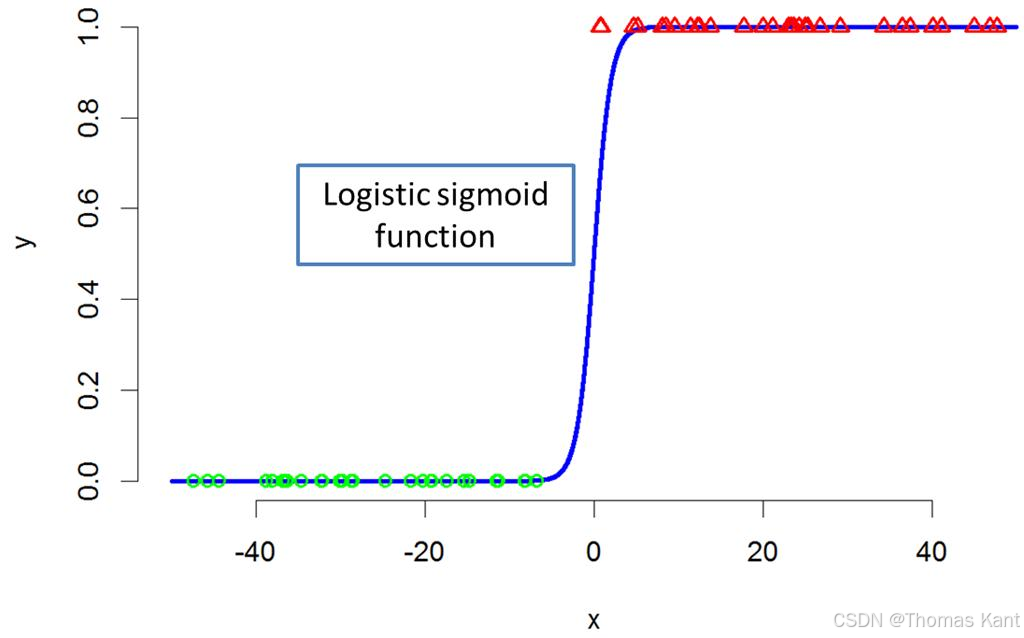
概率输出：逻辑回归通过 Sigmoid 函数将线性组合转换为概率值。Sigmoid 函数的表达式为： $σ(z)=11+e−z\sigma(z)=\frac{1}{1 + e^{-z}}$ ，其中 $z$ 是线性组合，即 $\theta^T x = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n$ ， $x$ 是输入特征向量， $θ\theta$ 是模型参数（权重和偏置）。通过 Sigmoid 函数，逻辑回归将线性回归的输出结果映射到 $(0, 1)$ 区间，这个区间内的值可以被理解为样本属于某一类别的概率。例如，在预测邮件是否为垃圾邮件时，逻辑回归模型输出的概率值为 0.8，就表示该邮件有 80% 的可能性是垃圾邮件。这种概率输出的特性使得我们可以根据实际需求灵活调整阈值，以满足不同的业务场景。如果我们对垃圾邮件的过滤要求非常严格，不希望有任何垃圾邮件进入收件箱，那么可以将阈值设置得较低，比如 0.3，只要模型预测为垃圾邮件的概率超过 0.3，就将其判定为垃圾邮件；如果我们更注重误判的情况，不希望将正常邮件误判为垃圾邮件，那么可以将阈值设置得较高，比如 0.7，只有当模型预测为垃圾邮件的概率超过 0.7 时，才将其判定为垃圾邮件。

计算高效：逻辑回归基于梯度下降的优化算法来寻找最优的模型参数。梯度下降算法的基本思想是通过迭代的方式，不断调整模型参数，使得损失函数的值最小化。在每一次迭代中，计算损失函数对于每个参数的偏导数，然后按照梯度的反方向更新参数的值。这种算法适用于大规模数据，因为它可以在每次迭代中使用部分样本数据来更新参数，而不需要使用整个数据集，从而大大减少了计算量。以一个包含数百万条样本数据的信用评估任务为例，使用逻辑回归模型基于梯度下降算法进行训练，在合理的时间内就可以得到较为准确的模型，并且能够快速地对新的客户数据进行信用评估。此外，为了进一步加快收敛速度，还可以对输入特征进行归一化处理，使得不同特征的尺度一致，避免某些特征对梯度的影响过大。

可解释性强：逻辑回归模型的特征系数直接反映了每个特征对类别预测的影响方向和程度。例如，在一个预测肿瘤是否为恶性的逻辑回归模型中，特征 “肿瘤大小” 对应的系数为正，且数值较大，这就表明肿瘤大小与肿瘤为恶性的概率呈正相关关系，即肿瘤越大，肿瘤为恶性的可能性就越高；而特征 “患者年龄” 对应的系数为负，说明年龄与肿瘤为恶性的概率呈负相关关系，年龄越小，肿瘤为恶性的可能性相对较低。这种可解释性使得我们能够清楚地了解模型是如何做出决策的，有助于业务人员理解数据背后的规律，从而更好地应用模型进行决策分析。相比之下，一些复杂的机器学习模型，如神经网络，虽然在某些任务上表现出色，但由于其模型结构复杂，内部参数众多，很难直观地解释模型的决策过程。

正则化支持：逻辑回归支持 L1 和 L2 正则化。L1 正则化是在损失函数中添加参数向量的 L1 范数（即各元素的绝对值之和）作为惩罚项，公式为 $L(w)=1N∑i=1n(f(xi;w)−yi)2+λ∣∣w∣∣1L(w)=\frac{1}{N}\sum_{i=1}^{n}(f(x_i;w)-y_i)^2+\lambda||w||_1$ ；L2 正则化是在损失函数中添加参数向量的 L2 范数（即各元素的平方和的平方根）作为惩罚项，公式为 $L(w)=1N∑i=1n(f(xi;w)−yi)2+λ2∣∣w∣∣2L(w)=\frac{1}{N}\sum_{i=1}^{n}(f(x_i;w)-y_i)^2+\frac{\lambda}{2}||w||^2$ ，其中 $λ\lambda$ 是正则化参数，用于控制正则化的强度。正则化的作用是限制模型的复杂度，防止过拟合。当模型出现过拟合时，它在训练集上表现很好，但在测试集或新数据上的性能较差。通过添加正则化项，可以使得模型在训练过程中更加关注参数的大小，避免某些参数过大，从而降低模型对训练数据中噪声和细节的过度拟合，提高模型的泛化能力。例如，在一个图像分类任务中，如果不使用正则化，逻辑回归模型可能会学习到训练集中图像的一些特殊噪声或局部特征，导致在测试集上的分类准确率下降；而使用 L2 正则化后，模型能够更好地捕捉图像的普遍特征，提高在不同图像上的分类性能。此外，L1 正则化还具有产生稀疏解的特性，即可以使部分参数变为 0，从而实现特征选择，去除一些不重要的特征，进一步简化模型。

二、逻辑回归的核心概念

2.1 从线性回归到分类模型

线性回归是一种广泛应用的回归分析方法，其基本公式为 $\theta^T \mathbf{x} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n$ ，其中 $,xn)T\mathbf{x} = (x_0, x_1, \cdots, x_n)^T$ 是输入特征向量， $x_0 = 1$