1354A - Alarm Clock[思维]
1354B - Ternary String[思维]
1354C1 - Simple Polygon Embedding[几何]
1354C2 - Not So Simple Polygon Embedding[几何]
1354D - Multiset[二分][树状数组]
1354E - Graph Coloring[
d
p
dp
dp][
01
01
01染色]
1354F - Summoning Minions[
d
p
dp
dp][费用流]
1354G - Find a Gift[ ]
1354A - Alarm Clock[思维]
题意
a、b、c、d 分别为
Polycarp必须睡眠才能感到精神振奋的时间、
第一个警报发出前的时间、
每个后续警报发出前的时间
Polycarp花在入睡上的时间。
一开始 Polycarp 先睡 b b b 分钟,接下来每段 c c c 分钟内,他需要消耗 d d d 分钟睡着
也就是说之后每段的睡眠时长最多为 c − d c - d c−d,并且他每次醒来都是 c c c 分钟后的事情了
问到最后睡足够时间下床需要多久
题目说的如果睡不到 1 1 1 分钟,就要继续睡,不到 1 1 1 分钟也就是 ≤ 0 \leq 0 ≤0,即 c ≤ d c \leq d c≤d 的意思
做法
首先扣掉 b b b
如果 a > 0 & & ( c − d ) ≤ 0 a > 0 \&\& (c-d) \leq 0 a>0&&(c−d)≤0,则不可能
否则输出 b + a / (c - d) * c + ( b + a / (c - d) * c != 0)
样例
Input
7
10 3 6 4
11 3 6 4
5 9 4 10
6 5 2 3
1 1 1 1
3947465 47342 338129 123123
234123843 13 361451236 361451000
Output
27
27
9
-1
1
6471793
358578060125049
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 5;
int main() {
int T;
scanf("%d", &T);
while(T--) {
ll a, b, c, d;
scanf("%lld%lld%lld%lld", &a, &b, &c, &d);
a -= b;
if(a <= 0) {
printf("%lld\n", b);
}else if(a > 0 && c <= d) {
puts("-1");
}else{
ll sum = b + a / (c - d) * c;
if(a % (c - d) != 0) sum += c;
printf("%lld\n", sum);
}
}
return 0;
}
1354B - Ternary String[思维]
题意
求包含 1 , 2 , 3 1, 2, 3 1,2,3 这三个数字每个数字数目至少 1 1 1 个,
的连续子串最短长度
做法
直接记录每个数字最后出现的位置
然后每次计算更新最短长度
样例
Input
7
123
12222133333332
112233
332211
12121212
333333
31121
Output
3
3
4
4
0
0
4
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 5;
const int inf = 0x3f3f3f3f;
char s[maxn];
int a[5];
int main() {
int T;
scanf("%d", &T);
while(T--) {
int ans = inf;
scanf("%s", s + 1);
int n = strlen(s + 1);
a[1] = a[2] = a[3] = 0;
for(int i = 1; i <= n; ++i) {
a[s[i] - '0'] = i;
if(a[1] && a[2] && a[3]) {
ans = min(ans, max(max(a[1], a[2]), a[3]) - min(min(a[1], a[2]), a[3]) + 1);
}
}
printf("%d\n", ans == inf ? 0 : ans);
}
return 0;
}
1354C1 - Simple Polygon Embedding[思维]
题意
求正 2 n 2n 2n 边形(边长为 1 1 1)的最小外接正方形的边长,保证 n n n 为偶数
做法
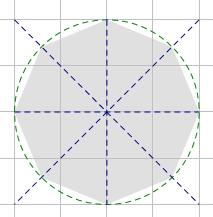
偶数的画法比较容易想到:
例如 n = 4 n = 4 n=4 的情况
把与线相连的交点连起来
覆盖正多边形的一条边开始画正方形
θ = 180 ∗ ( 2 n − 2 ) 4 n ∗ 1 180 ∗ 1 π \theta = \frac{180*(2n-2)}{4n} * \frac{1}{180} * \frac{1}{\pi} θ=4n180∗(2n−2)∗1801∗π1
前面是计算三角形内角总和,然后求出 θ \theta θ
后面这一步是为了转换成弧度制,因为 t a n tan tan 是弧度制的
a 1 = t a n ( θ ) \frac{a}{1} = tan(\theta) 1a=tan(θ)
样例
Input
3
2
4
200
Output
1.000000000
2.414213562
127.321336469
代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn = 2e5 + 5;
const int inf = 0x3f3f3f3f;
const double pi = acos(-1.0);
int main() {
int T;
scanf("%d", &T);
while(T--) {
double n, ans;
scanf("%lf", &n);
ans = 180.0 * (2.0 * n - 2.0) / (4.0 * n);
ans = tan(ans / 180.0 * pi);
printf("%.8f\n", ans);
}
return 0;
}
1354C2 - Not So Simple Polygon Embedding[思维]
参考链接:
Not So Simple Polygon Embedding
题意
求正 2 n 2n 2n 边形(边长为 1 1 1)的最小外接正方形的边长,保证 n n n 为奇数
做法
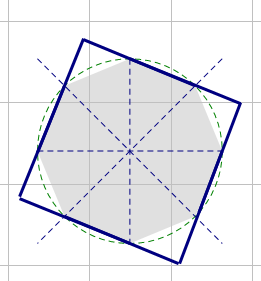
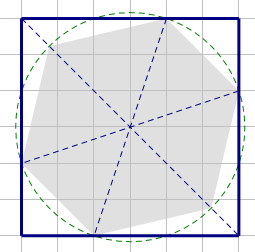
例如 n = 3 n = 3 n=3,先平分成 6 6 6 个角
画个圆
连接交点
$ θ = 360 2 ∗ n ∗ π 180 \theta = \frac{360}{2*n} * \frac{\pi}{180} θ=2∗n360∗180π
1 2 = x ∗ s i n ( θ 2 ) \frac{1}{2} = x * sin(\frac{\theta}{2}) 21=x∗sin(2θ), 得到 x x x
正弦定理: t 1 s i n ( θ ) = x s i n ( π 4 ) \frac{t1}{sin(\theta)} = \frac{x}{sin(\frac{\pi}{4})} sin(θ)t1=sin(4π)x
t 2 s i n ( π 2 − θ ) = x s i n ( π 4 ) \frac{t2}{sin(\frac{\pi}{2}-\theta)} = \frac{x}{sin(\frac{\pi}{4})} sin(2π−θ)t2=sin(4π)x
a = t 1 + t 2 a = t1 + t2 a=t1+t2
样例
Input
3
3
5
199
Output
1.931851653
3.196226611
126.687663595
代码
...不是很理解
为什么模拟出来最后一个是错的
头大
const double pi = acos(-1.0);
int main() {
int T;
scanf("%d", &T);
while(T--) {
double n, angle, x, a;
scanf("%lf", &n);
angle = 360.0 / 2.0 / n / 180 * pi;
x = 0.5 / sin(angle * 0.5) / sin(pi/4);
a = x * sin(angle) + x * cos(angle);
printf("%.8f\n", a);
}
return 0;
}





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








