关系模式
关系的例子
- 关系模型是目前广泛应用的数据模型
- 由表的集合构成
例如
| ID | name | dpt_name | salary |
|---|---|---|---|
| 11111 | JAM | CS | 12345 |
- 元组 tuple:表中的一行,元素无所谓
- 属性 attribute : 原子的,不可再分的,要有属性域,如上表的name,dept_name,salary
1. 空值表示特殊值,表示这个属性未知or不存在
另外的例子
关系模式可以表示成
R(A1,A2,…,An)R(A_1,A_2,…,A_n)R(A1,A2,…,An)
- A1,A2,…AnA_1,A_2,…A_nA1,A2,…An表示属性
- 如 instructor(ID, name, dept_name, salary)
- 如 department(dept_name, building, budget)
- 关系模式中,相同属性可以把不同关系的元组联系起来
关系模式与实例
- 关系模式:关系的逻辑设计
- 关系实例:给定时刻关系中数据的快照
- 数据库模式versus 数据库实例 ——类比——> 类型与变量
关系模式不常变化,关系实例常变化。(可以参考第7版教科书32页的图2-9)
Keys(键与码)
KKK是唯一识别关系r(R)r(R)r(R)中的一个元组,称KKK是关系r(R)r(R)r(R)的超码(Superkey)
- KKK是一个或多个属性的集合,K⊆RK\sube RK⊆R
(RRR是关系模式rrr的属性集合 ) - 超码可能包含无关紧要的属性
- K的任意超集也是超码
如 {ID}和{ID, name}是instructor的超码
候选码与主码
任意真子集不能称为超码的最小超码为候选码
如{ID}是instructor的候选码
若{name, dept_name}可以唯一确定instructor的各成员,那他也是候选码
于是需要选择其中一个候选码作为主码(primary key)
外码
一个关系模式(r1)(r_1)(r1)在其属性上包含另一个关系模式(r2)(r_2)(r2)的主码,此属性在rir_iri上称为参照r2r_2r2的外码(foreign key), r1r_1r1称为外码依赖的参照关系
如 dept_name是instructor的外码
参照完整性约束
参照关系中任意元组在 特定属性(如外码) 的取值,必须等于被参照关系中某个元组在 此特定元素 上的取值
例外:外码约束
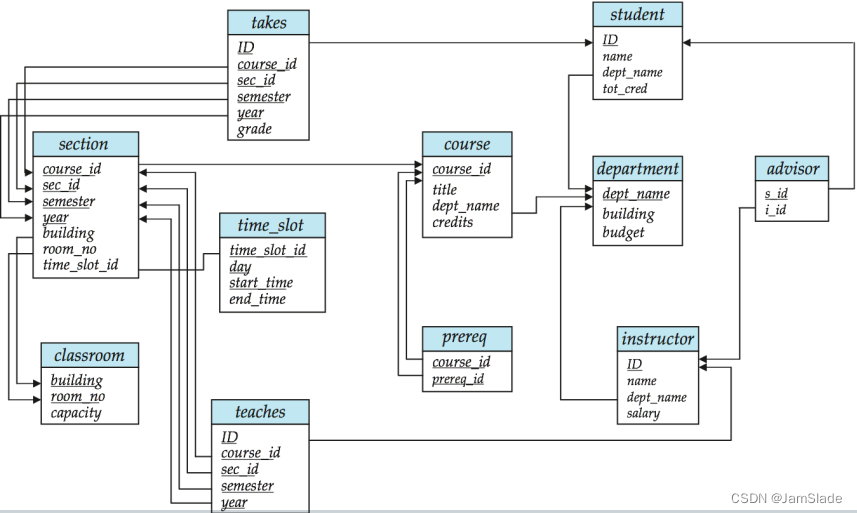
模式图
一个含主码与外码依赖的数据库可用模式图表示
- 一个关系模式用一个矩形表示
- 主码用下划线标注
- 外码约束(依赖)用 从参照关系的外码到被参照关系的主码之间的 箭头表示
关系查询语言
分过程化语言与非过程化语言
纯查询语言
- 关系代数 – 过程化
- 元组关系演算 – 非过程化
- 域关系演算 – 非过程化
所有过程化查询语言(如关系代数)都提供一组关系运算,施加于单个关系上或一对关系上,结果为单个关系
关系代数
基本关系运算
| 选择 | σ\sigmaσ | 一元 |
| 投影 | Π\PiΠ | 一元 |
| 并 | ∪\cup∪ | 二元 |
| 差 | −-− | 二元 |
| 笛卡尔积 | ×\times× | 二元 |
| 更名 | ρ\rhoρ | 一元 |
交连接赋值都可由上述内容引申
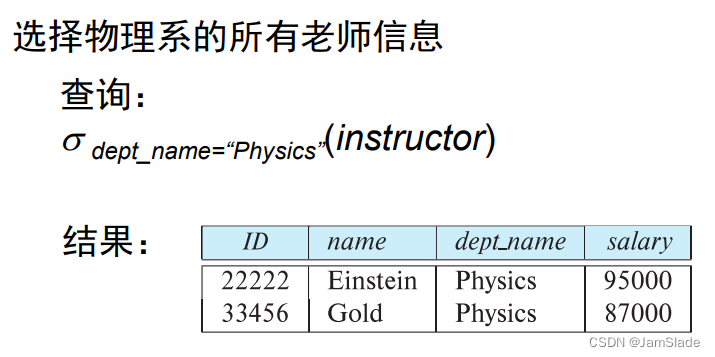
选择
选择满足给定为此的元组
σp(r)\sigma_p(r)σp(r)
其中ppp是选择谓词
σp(r)={t∣t∈r∧p(t)}\sigma_p(r) = \{t|t\in r\land p(t) \}σp(r)={t∣t∈r∧p(t)}
- p是一个or多个元组选择条件组成的为此,由∧∨¬\land\quad\lor\quad\lnot∧∨¬连接
- p可包含两个属性的比较,如a=b
- 条件可以表示为<属性>/<常量>"opreation"<属性>/<常量><属性>/<常量> "opreation" <属性>/<常量><属性>/<常量>"opreation"<属性>/<常量>, operation表示比较运算符的一种
总的来说,就是在最后显示的时候只显示其中某些行。
投影
过滤掉特定元素
ΠA1,A2,…,Am(r)\Pi_{A_1,A_2,…,A_m}(r)ΠA1,A2,…,Am(r)
AiA_iAi属性名,rrr是关系名
通过去除未列出的列,获得的一个m 列的关系

对比
σ去除的是行,Π去除列\sigma去除的是行,\Pi去除列σ去除的是行,Π去除列
笛卡尔积
结合来自任意两个关系的信息
表示r×sr\times sr×s
由于相同属性名可能同时出现在r(R)r(R)r(R),s(S)s(S)s(S),所以在这个过程中需要rename以区别这些属性
r×s={<t,q>∣t∈r∧q∈s}r\times s = \{<t,q>|t\in r\land q\in s\}r×s={<t,q>∣t∈r∧q∈s}
r有n列m行数据,k有i列j行数据
r×k有n+i列,m×k行r\times k 有n+i列,m\times k 行r×k有n+i列,m×k行
连接运算
r⋈θs=σθ(r×s)r\Join_\theta s = \sigma_\theta(r\times s)r⋈θs=σθ(r×s)
θ\thetaθ是R∪SR\cup SR∪S模式属性上的一个选择谓词

并运算
符号表示r∪s={t∣t∈r∨t∈s}r\cup s = \{t|t\in r\lor t\in s\}r∪s={t∣t∈r∨t∈s}
如果要让r∪sr\cup sr∪s有意义,要求两个条件成立
- rrr和sss必须同元——属性数目相同
- 属性域相同
本质上是加行
差
r−s={t∣t∈r∧t∉s}r-s = \{t|t\in r\land t\notin s\}r−s={t∣t∈r∧t∈/s}
要求同并运算
本质上就是减行
更名运算
px(E)p_x(E)px(E)
返回表达式E的结果并把名字x赋予给他
若表达式E是多元的,可以设置
px(A1,A2,...,An)(E)p_{x(A_1,A_2,...,A_n)}(E)px(A1,A2,...,An)(E)
返回E的结果,赋予名字x,各属性更名为AiA_iAi

总结与其他关系运算
基本表达式是如下二者之一:
- 数据库的一个关系
- 一个常数关系
其他附加关系运算
不增强关系代数表达能力,但可简化查询
- 交 r∩s={t∣t∈r∧t∈s}=r−(r−s)r\cap s = \{t|t\in r \land t \in s\} = r-(r-s)r∩s={t∣t∈r∧t∈s}=r−(r−s),使用要求同并
- 赋值 r←sr\leftarrow sr←s
将查询表达为一个顺序程序,包括
✓一系列的赋值
✓一个值被做为查询结果显示的表达式
➢ 赋值赋给一个临时关系变量,并不修改数据库关系实例
➢ 赋值赋给一个数据库关系,修改数据库关系实例 - 连接
如R=(A,B,C,D)S=(E,B,D)R = (A,B,C,D)\quad S=(E,B,D)R=(A,B,C,D)S=(E,B,D)
r⋈s=Πr.A,r.B,r.C,r.D,s.E(σr.B=s.B∧r.D=s.D(r×s))r\Join s = \Pi_{r.A,r.B,r.C,r.D,s.E}(\sigma_{r.B=s.B\land r.D = s.D}(r\times s))r⋈s=Πr.A,r.B,r.C,r.D,s.E(σr.B=s.B∧r.D=s.D(r×s)) - 除 ÷\div÷
- 外连接
交
r∩s={t∣t∈r∧t∈s}r\cap s = \{t| t\in r\land t\in s\}r∩s={t∣t∈r∧t∈s}
等价于
r∩s=r−(r−s)r\cap s = r-(r-s) r∩s=r−(r−s)
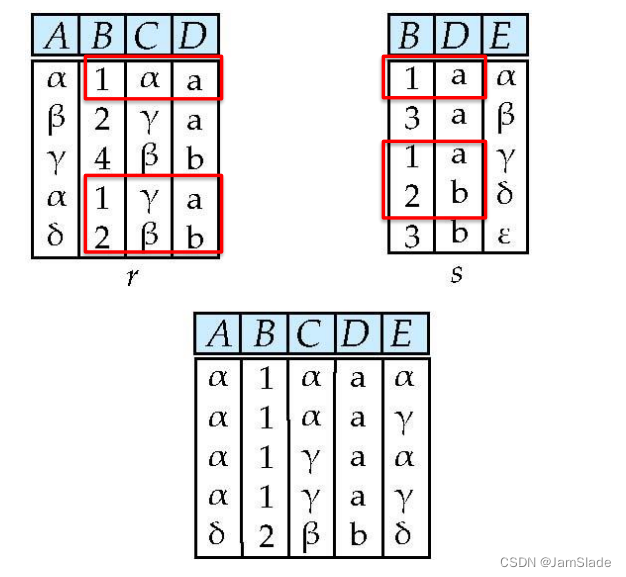
自然连接(不是连接
如果r和s中有名字相同的列,那么需要先检验这些列内的数据是否一致,将一致的数据额外加上两个集合中都没有的列
R = (A, B, C, D)
✓ S = (E, B, D)
✓ 自然连接结果的关系模式为(A, B, C, D, E)
(如果是连接时 A,B,C,D,E,B,D)
r⋈s=Πr.A,r.B,r.C,r.D,s.E(σr.B=s.B,r.D=s.B(r×s))r\Join s = \Pi_{r.A, r.B, r.C, r.D, s.E}(\sigma_{r.B= s.B, r.D=s.B}(r\times s))r⋈s=Πr.A,r.B,r.C,r.D,s.E(σr.B=s.B,r.D=s.B(r×s))
赋值
赋值操作(←\leftarrow←)可以使复杂查询的表达变得简单,即将查询表达为
一个顺序程序,包括
✓一系列的赋值
✓一个值被做为查询结果显示的表达式
➢ 赋值赋给一个临时关系变量,并不修改数据库关系实例
➢ 赋值赋给一个数据库关系,修改数据库关系实例
除
参考乘的逆运算即可

Conclusion






 本文介绍了关系模型的基本概念,包括关系模式、实例、键、外码及关系查询语言等内容,并详细解释了关系代数中的各种运算。
本文介绍了关系模型的基本概念,包括关系模式、实例、键、外码及关系查询语言等内容,并详细解释了关系代数中的各种运算。

















 494
494

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








