课后自主练习（进制）1015. n! 进制 easy《编程思维与实践》个人学习笔记

最新推荐文章于 2023-05-12 13:47:13 发布

原创最新推荐文章于 2023-05-12 13:47:13 发布 · 172 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

编程思维与实践专栏收录该内容

109 篇文章

订阅专栏

本文介绍了一种将十进制数转换为九进制阶乘表示的算法实现，通过特殊的递归处理方法解决了传统转换过程中遇到的问题，并提供了一个具体的C++实现案例。

题目

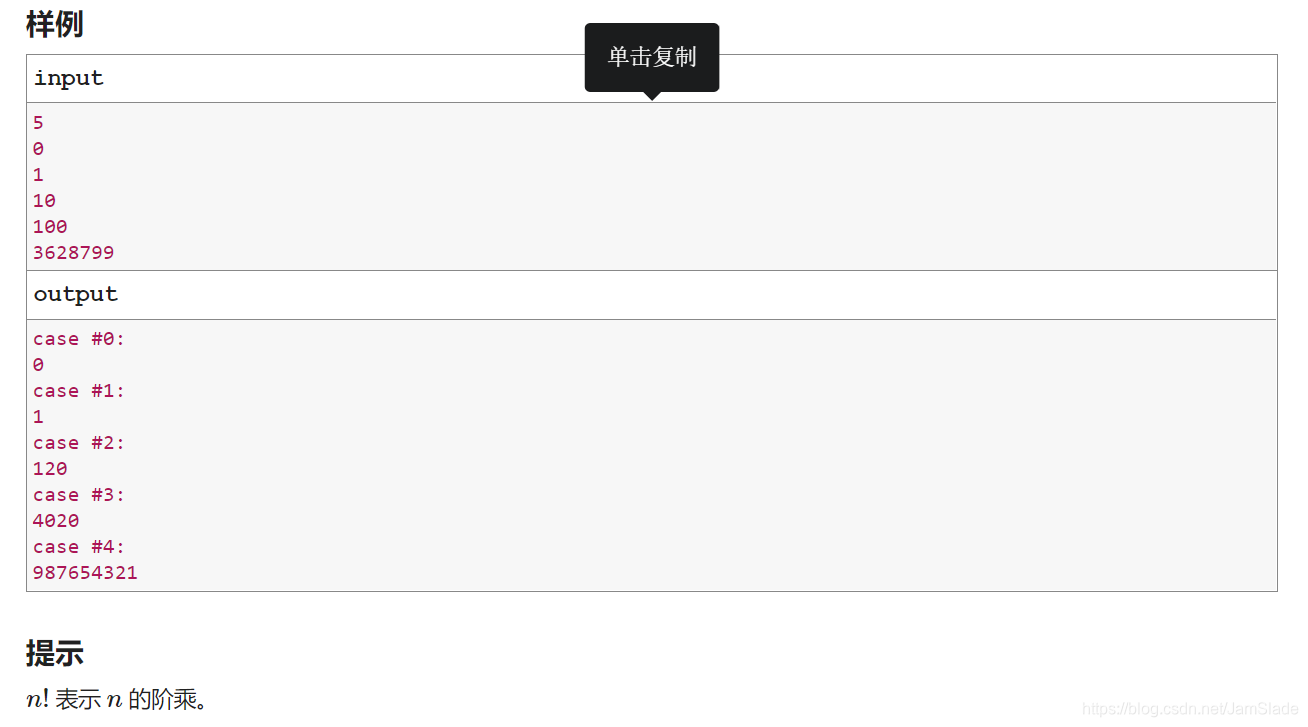
在这里插入图片描述

思路

相比于之前的转化其他普通进制来说，需要特别注意mod n!可能会出现大于十进制的数字，因此我们得特殊处理一下，直接
数字 - （进制 ✖ （数字 / n！））
来获取（数字 / n！）作为 n!进制下对应的数字，剩下的数字继续来递归

代码

#include<iostream>
#include<stack>
using namespace std;

void trans(long long a)
{
    long nbase[10];
    long base = 1;
    for(int i = 1; i <= 9; i++)
    {
        base *= i;
        nbase[i] = base;  
    }

    int flag = 0;
    for(int i = 9; i > 0; i--)
    {
        int temp = a / nbase[i];//对应的几！进制下可以出现数字几
        if(temp != 0)//注意到前面可能有0
        {
            cout << temp;
            flag = 1;//保证后面的0可以输出
            a = a - temp * nbase[i];//注意n！进制要如何减少 
        }                           //以前可以直接除以来减少，但是这里的n!进制每次除都不同，所以最方便还是直接减
        else
        {
            if(flag)
            {
                cout << temp;
            }
        }
        

    }
    cout << endl;
}

int main()
{
    int total;
    cin >> total;

    for(int i = 0 ; i < total; i++)
    {
        long long a;
        cin >> a;
        cout << "case #" << i<<":"<<endl;
        trans(a);
    }
    
}