Codeforces Round #197 (Div. 2): D. Xenia and Bit Operations（线段树）

Jaihk662

于 2018-07-24 17:54:23 发布

阅读量333

点赞数 1

CC 4.0 BY-SA版权

分类专栏： ☆ACM☆ 文章标签： codeforces

本文链接：https://blog.youkuaiyun.com/Jaihk662/article/details/81189398

☆ACM☆ 专栏收录该内容

222 篇文章

订阅专栏

本文介绍了一种使用线段树进行单点更新的算法，该算法适用于处理长度为2^n的序列，并能高效地进行多次修改操作，每次修改后都能快速计算出序列的值。通过交替使用或运算和异或运算，最终得到序列的单一数值表示。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

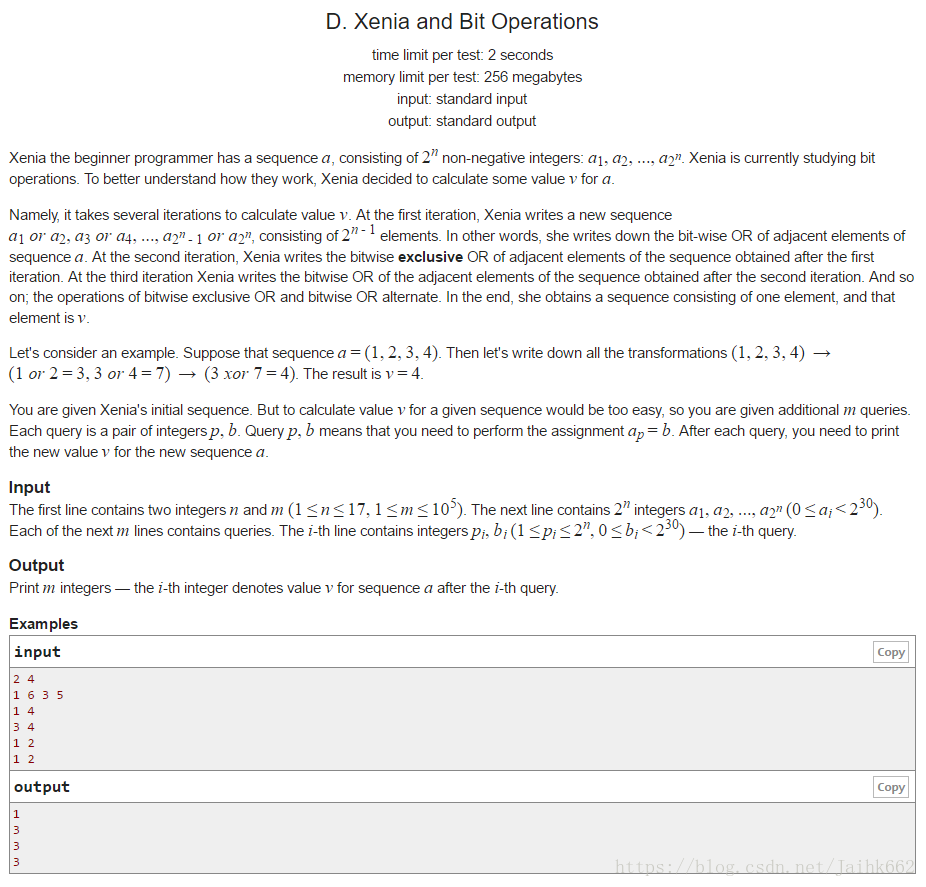
题意：定义一个长度2^n的序列{a1, a2…an}，序列相邻两个元素或运算之后再进行异或运算再进行或运算（两种运算交替进行）直到只剩下一个数字，这个数字即为序列的值，输入第一行两个数n，m表示序列的长度为2^n，m次修改，每次修改a, b表示将位置a上的数修改为b，对于每次修改输出修改后序列的值

看明白了之后你会发现这就是线段树单点更新

#include<stdio.h>
int tre[444444], p[444444] = {1};
void Create(int l, int r, int x)
{
	int m;
	if(l==r)
	{
		scanf("%d", &tre[x]);
		return;
	}
	m = (l+r)>>1;
	Create(l, m, x*2);
	Create(m+1, r, x*2+1);
	if(p[r-l+1])
		tre[x] = tre[x*2]|tre[x*2+1];
	else
		tre[x] = tre[x*2]^tre[x*2+1];
}
void Update(int l, int r, int x, int a, int b)
{
	int m;
	if(l==r)
	{
		tre[x] = b;
		return;
	}
	m = (l+r)>>1;
	if(a<=m)
		Update(l, m, x*2, a, b);
	else
		Update(m+1, r, x*2+1, a, b);
	if(p[r-l+1])
		tre[x] = tre[x*2]|tre[x*2+1];
	else
		tre[x] = tre[x*2]^tre[x*2+1];
}
int main(void)
{
	int n, m, i, x, y;
	scanf("%d%d", &n, &m);
	n = (1<<n);
	for(i=1;i<=n;i<<=1)
		p[i] = p[i>>1]^1;
	Create(1, n, 1);
	while(m--)
	{
		scanf("%d%d", &x, &y);
		Update(1, n, 1, x, y);
		printf("%d\n", tre[1]);
	}
	return 0;
}