今天研究了一下遗传算法,发现原理还是很好懂的,不过在应用层面上还是有很多要学习的方法,如何定义编码解码的过程,如何进行选择和交叉变异,这都是我们需要解决的事情,估计还是要多学多用才能学会,当然了如果大家对我写的这些内容如果有什么不同的看法的话也建议大家提出,毕竟算法小白一个。
遗传算法介绍
所谓遗传算法其实就是一种仿生算法,一种仿生全局优化算法模仿生物的遗传进化原理,通过自然选择(selection)、交叉(crossover)与变异(mutation)等操作机制,逐步淘汰掉适应度不够高的个体,使种群中个体的适应性(fitness)不断提高。
核心思想:物竞天择,适者生存

主要的一些应用领域主要是在
- 函数优化,求函数极值类
- 组合优化(旅行商问题一已成为衡 量算法优劣的标准、背包问题、装箱问题等)
- 生产调度问题,配送问题
- 自动控制(如航空控制系统的优化设计、模糊控制器优化设计和在线修改隶属度函数、神经网络结构优化设计和调整神经网络的连接权等优化问题)
- 机器人智能控制(如移动机器人路径规划、关节机器人运动轨迹规划、机器人逆运动学求解等)
- 图像处理和模式识别(如图像恢复、图像边缘特征提取、几何形状识别等)
- 机器学习(将GA用 于知识获取,构建基于GA的机器学习系统等)
大概数学建模里面的话,主要就是组合优化问题,迭代问题,调度问题,机器学习吧
遗传算法流程
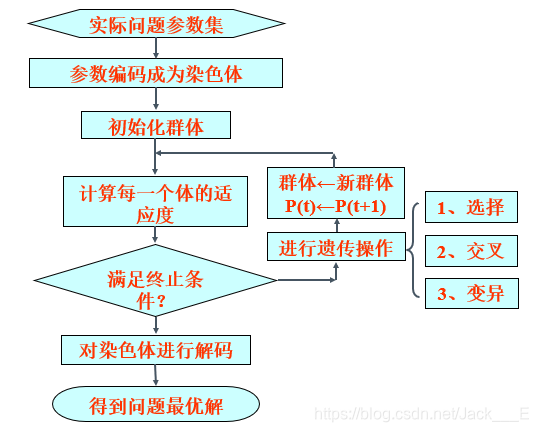
- 适应度 :用于筛选各种解向量的指标,如果有多个指标应该是需要对这些指标进行统一处理的,最后是能变成一个统一的能消除不同量纲差异的函数表达式,要根据题目所给的条件来分析。
- 编码 :编码的过程主要就是对题目的一组解将他进行数据化成一段DNA序列,也就是利用矩阵,解向量等方式准确地表示出我们的这组解的特征。
- 解码 :解码主要是能够解析我们编码后的DNA序列,然后讲其表示的信息还原出来,然后进行适应度的计算。
- 自然选择 :自然选择主要是依据个体适应度的大小转化成被选择的概率,利用轮盘赌的方式——将数据按照指定的概率分布方式提取出来,从而实现了物竞天择适者生存的原理,适应度大的个体被留下来的概率会逐步增大。
- 变异 :随机修改某一位基因序列,从而改变他的适应度
- 交叉重组 :种群中随机选取两个个体,交互若干的DNA片段,从而改变他的适应度,生成新的子代
这里我们要明白的一点就是,遗传算法只是提供了一个迭代的模板,具体的适应度函数也就是我们选择优化的相关指标和他的表示都是需要根据题目里面的问题来建模,然后编码解码的方式说白了其实就是如何表示我们要的可行解,比如说求一个函数的极值且精确到多少位那么他的可行解就是自变量,这里我们通常采用二进制编码,如果是TSP问题,那么可行解就可以表示成为各个配送点编号构成的一个数组,进行实数数组序列的方式编码,自然而然解码的方法和含义我们也都清楚了
求函数极值的问题
这里是我根据网上莫烦的python视频教程,来写的一个算法,这里我们要做的问题是求出 f ( x ) = s i n ( 10 x ) × x + c o s ( 2 x ) × x f(x)=sin(10x)×x+cos(2x)×x f(x)=sin(10x)×x+cos(2x)×x的极大值。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
DNA_SIZE=10 #编码DNA的长度
POP_SIZE=100 #初始化种群的大小
CROSS_RATE=0.8 #DNA交叉概率
MUTATION_RATE=0.003 #DNA变异概率
N_GENERATIONS=200 #迭代次数
X_BOUND=[0,5] #x upper and lower bounds x的区间
def F(x):
return np.sin(10*x)*x+np.cos(2*x)*x
def get_fitness(pred):
return pred+1e-3-np.min(pred)
#获得适应值,这里是与min比较,越大则适应度越大,便于我们寻找最大值,为了防止结果为0特意加了一个较小的数来作为偏正
def translateDNA(pop):#DNA的二进制序列映射到x范围内
return pop.dot(2 ** np.arange(DNA_SIZE)[::-1]) / float(2**DNA_SIZE-1) * (X_BOUND[1]-X_BOUND[0])
def select(pop,fitness):
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=fitness / fitness.sum())
#我们只要按照适应程度 fitness 来选 pop 中的 parent 就好. fitness 越大, 越有可能被选到.
return pop[idx]
#交叉
def crossover(parent,pop):
if np.random.rand() < CROSS_RATE:
i_ = np.random.randint(0, POP_SIZE, size=1) # 选择一个母本的index
print("i_:",i_)
print("i_.size:",i_.size)
cross_points = np.random.randint(0, 2, size=DNA_SIZE).astype(np.bool) # choose crossover points
print("cross_point",cross_points)
print("corsssize:",cross_points.size)
print(parent[cross_points])
print(pop[i_, cross_points])
parent[cross_points] = pop[i_, cross_points] # mating and produce one child
print(parent[cross_points])
return parent
#变异
def mutate(child):
for point in range(DNA_SIZE):
if np.random.rand() < MUTATION_RATE:
child[point] = 1 if child[point] == 0 else 0
return child
pop = np.random.randint(2, size=(POP_SIZE, DNA_SIZE)) # initialize the pop DNA
plt.ion() # something about plotting
x = np.linspace(*X_BOUND, 200)
plt.plot(x, F(x))
for _ in range(N_GENERATIONS):
F_values = F(translateDNA(pop)) # compute function value by extracting DNA
# something about plotting
# if 'sca' in globals():
# sca.remove()
# sca = plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5)
# plt.pause(0.05)
# GA part (evolution)
fitness = get_fitness(F_values)
print("Most fitted DNA: ", pop[np.argmax(fitness), :])
pop = select(pop, fitness)
pop_copy = pop.copy()
for parent in pop:
child = crossover(parent, pop_copy)
child = mutate(child)
parent[:] = child # parent is replaced by its child
plt.scatter(translateDNA(pop), F_values, s=200, lw=0, c='red', alpha=0.5)
print("x:",translateDNA(pop))
print(type(translateDNA(pop)))
print(len(translateDNA(pop)))
print("max:",F_values)
plt.ioff()
plt.show()
最后我们可以展示一个结果,注意这个看似只有一个红点,其实这是100个种群个体集中得到的结果。,所以你最后打印的时候是一个100个解构成的1×100的解向量,最终都集中到了这个极值附近。

轮盘赌说的很复杂其实在python的random函数里可以说是封装好了,这里我们可以着重看看这个choice函数
np.random.choice(a, size=None, replace=True, p=None)
a表示我们需要选取的数组。
size表示我们需要提取的数据个数。
replace 代表的意思是抽样之后还放不放回去,如果是False的话,抽取不放回,如果是True的话, 抽取放回。
p表示的就是概率数组,代表每一个数被抽取出来的概率。
在我们代码中是写的
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=fitness / fitness.sum())
直接就抽取出了种群pop中每个个体的下标编号,这里我们的概率数组是使用的按照比例的适应度分配比例方法提取,而概率是以这种方式来建模计算的。
P
i
=
f
i
t
n
e
s
s
(
i
)
∑
i
=
0
n
f
i
t
n
e
s
s
(
i
)
P_{i}=\frac{fitness(i)}{\sum_{i=0}^{n}{fitness(i)}}
Pi=∑i=0nfitness(i)fitness(i)

求解TSP最短路的问题
tsp问题主要就是用户从某一起点出发然后经过所有的点一次并回到起点的最短路径,同时约定任意两点之前是互通可达的,我们要注意的是,可能两点之间的距离有时候是欧式距离,有的时候可能是哈密顿距离,自己要根据题意去判断。
这里我们主要讲解一下他的fitness函数主要是最短路径的总距离,编码序列则是最短路的编号,然后我们要注意这个问题在交叉变异的时候,我们一定要保证他首先是一条正确的可行解!不要出现有顶点重合或缺失的情况。
这里我们在解决交叉的时候是先随机选取一部分父类的基因编号,然后再从母本的DNA序列里面选出子类中缺少的基因,从而获得基因重组。
而变异的时候也不同于例1里面的修改二进制编码,而是采用的调换两个基因序号来完成,从而保证我们的结果一定是一条规范正确的回路。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
N_CITIES = 20 # 城市数量
CROSS_RATE = 0.1 #交叉概率
MUTATE_RATE = 0.02 #变异概率
POP_SIZE = 500 #种群概率
N_GENERATIONS = 500 #迭代次数
class GA(object):
def __init__(self, DNA_size, cross_rate, mutation_rate, pop_size, ):
self.DNA_size = DNA_size
self.cross_rate = cross_rate
self.mutate_rate = mutation_rate
self.pop_size = pop_size
self.pop = np.vstack([np.random.permutation(DNA_size) for _ in range(pop_size)])
def translateDNA(self, DNA, city_position): # get cities' coord in order
line_x = np.empty_like(DNA, dtype=np.float64)
line_y = np.empty_like(DNA, dtype=np.float64)
for i, d in enumerate(DNA):
city_coord = city_position[d]
line_x[i, :] = city_coord[:, 0]
line_y[i, :] = city_coord[:, 1]
return line_x, line_y
def get_fitness(self, line_x, line_y):
total_distance = np.empty((line_x.shape[0],), dtype=np.float64)
for i, (xs, ys) in enumerate(zip(line_x, line_y)):
total_distance[i] = np.sum(np.sqrt(np.square(np.diff(xs)) + np.square(np.diff(ys))))
fitness = np.exp(self.DNA_size * 2 / total_distance)#把欧氏距离的影响扩大化
return fitness, total_distance
def select(self, fitness):
idx = np.random.choice(np.arange(self.pop_size), size=self.pop_size, replace=True, p=fitness / fitness.sum())
return self.pop[idx]
def crossover(self, parent, pop):
if np.random.rand() < self.cross_rate:
i_ = np.random.randint(0, self.pop_size, size=1) # select another individual from pop
cross_points = np.random.randint(0, 2, self.DNA_size).astype(np.bool) # choose crossover points
keep_city = parent[~cross_points] # find the city number
swap_city = pop[i_, np.isin(pop[i_].ravel(), keep_city, invert=True)]
parent[:] = np.concatenate((keep_city, swap_city))
return parent
def mutate(self, child):
for point in range(self.DNA_size):
if np.random.rand() < self.mutate_rate:
swap_point = np.random.randint(0, self.DNA_size)
swapA, swapB = child[point], child[swap_point]
child[point], child[swap_point] = swapB, swapA
return child
def evolve(self, fitness):
pop = self.select(fitness)
pop_copy = pop.copy()
for parent in pop: # for every parent
child = self.crossover(parent, pop_copy)
child = self.mutate(child)
parent[:] = child
self.pop = pop
class TravelSalesPerson(object):
def __init__(self, n_cities):
self.city_position = np.random.rand(n_cities, 2)
plt.ion()
def plotting(self, lx, ly, total_d):
plt.cla()
plt.scatter(self.city_position[:, 0].T, self.city_position[:, 1].T, s=100, c='k')
plt.plot(lx.T, ly.T, 'r-')
plt.text(-0.05, -0.05, "Total distance=%.2f" % total_d, fontdict={'size': 20, 'color': 'red'})
plt.xlim((-0.1, 1.1))
plt.ylim((-0.1, 1.1))
plt.pause(0.01)
ga = GA(DNA_size=N_CITIES, cross_rate=CROSS_RATE, mutation_rate=MUTATE_RATE, pop_size=POP_SIZE)
env = TravelSalesPerson(N_CITIES)
for generation in range(N_GENERATIONS):
lx, ly = ga.translateDNA(ga.pop, env.city_position)#city_position(x,y)
fitness, total_distance = ga.get_fitness(lx, ly)#根据获得的路径计算路程
ga.evolve(fitness)
best_idx = np.argmax(fitness)
print('Gen:', generation, '| best fit: %.2f' % fitness[best_idx],)
# env.plotting(lx[best_idx], ly[best_idx], total_distance[best_idx])
env.plotting(lx[best_idx], ly[best_idx], total_distance[best_idx])
plt.ioff()
plt.show()

在最后我附上我学习的这个视频教程吧,多看看知乎csdn还有很多解释。明天我的京东快递《matlab智能算法30个案例分析》就要到了,真的是本好书,顺带一提学校培训真累啊,还啥都不会。
莫烦python遗传算法




















 7097
7097










