chapter-4-介绍神经网络

反向传播

首先介绍一个概念：计算图。简单来说，计算图是一个函数的可视化表达，如下图：

其中每个节点代表一个计算。

利用计算图，我们可以很容易地使用反向传播的思想计算每个变量的梯度：

首先我们在每个运算后定义一个变量来保存其对应的运算结果，如上图的q和f；然后我们从后向前地分别计算每个运算结果对其上一级变量的导数，如df/dq、df/dz、dq/dx；依次这样做，直到到达了计算图的最前面，即输入数据处。此时计算结果对应输入数据的导数，即df/dx时，利用链式求导法则，只需一路将从f到x的路径上的导数相乘即可。

一个稍复杂的例子如下图：

值得注意的一点是，这里可以聚合几个运算，把它们视作一个运算进行处理。这是因为sigmoid函数的有着非常优美的求导结果。这种处理方式可以简化神经网络，或许也能减少算法的运算时间。

这里举出了一个包含矩阵的计算图计算的例子：

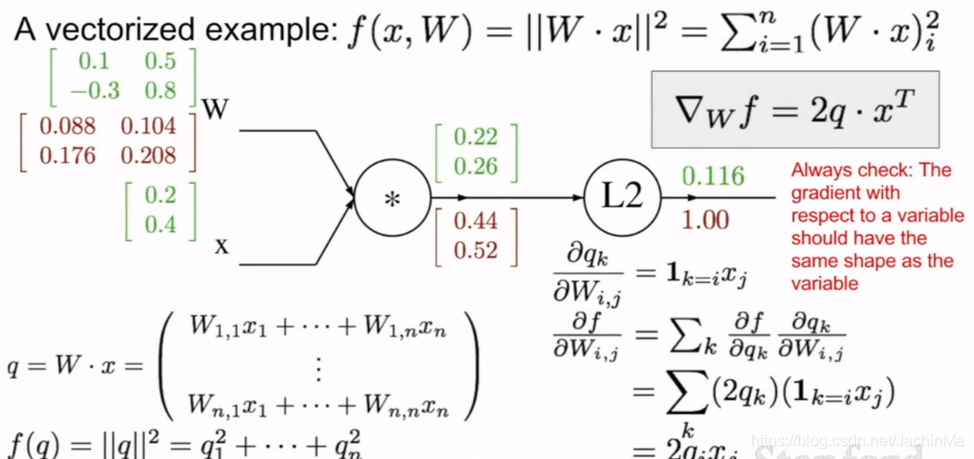
思路我还是理解的，不过这里矩阵对矩阵的求导没看懂，看了一圈也没有解释清楚的，后续如果实践中遇到这个问题的话还是要找书看一下。

神经网络

课程这里的介绍过于抽象，下面的介绍可能简单些：

https://blog.youkuaiyun.com/JachinMa/article/details/90050136
https://blog.youkuaiyun.com/JachinMa/article/details/90092536

从函数的思想，神经网络就是有一些被层次化的方式在顶层被堆叠在一起的简单的线性函数，进而组合成一个非线性函数。

但要注意，虽然将神经网络与真实的生物神经网络做对比是理解神经网络的一个好方法，但由于生物神经网络的极度复杂性，我们应该认识到目前的神经网络算法离生物神经网络还有着非常远的距离。