一、最长公共子序列(LCS)是什么?
看一个例子:S1={1,5,2,8,9,3,6},S2={5,6,8,9,3,7},其最长公共子序列为{5,8,9,3}。
注意:最长公共子串和最长公共子序列是不同的。顾名思义,前者必须是连续的,后者只要求顺序一样即可。
二、如何解决?
1.分析问题
设序列S1={x1,x2,…,xn} 和 S2={y1,y2,…,ym} 的最长公共子序列为 S={z1,z2,…,zk}。
我们首先分析两个序列 S1,S2 的最后一个元素 xn, ym。
1)若 xn = ym,则这俩元素都一定属于序列S,即 xn = ym = zk;
2)若xn ≠ ym,且 zk ≠ xn,则 S[k] 是 S1[n-1] 和 S2[m] 的最长公共子序列;
3)若xn ≠ ym,且 zk ≠ ym,则 S[k] 是 S1[n] 和 S2[m-1] 的最长公共子序列;
2.递推公式

根据dp[][]间的对应位置关系,存储到 b 数组中,详见代码:

for(int i=1;i<=n;i++) c[i][0]=0;
for(int j=1;j<=m;j++) c[0][j]=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(S1[i]==S2[j]){xiexiangshangjiantou
dp[i][j]=dp[i-1][j-1]+1;
b[i][j]=1; //1代表“↖”
}
else if(dp[i-1][j]>dp[i][j-1]){
dp[i][j]=dp[i-1][j];
b[i][j]=2; //2代表“↑”
}
else{
dp[i][j]=dp[i][j-1];
b[i][j]=3; //3代表“←”
}
}
}
下图为求解最大公共子序列 S 长度的图解
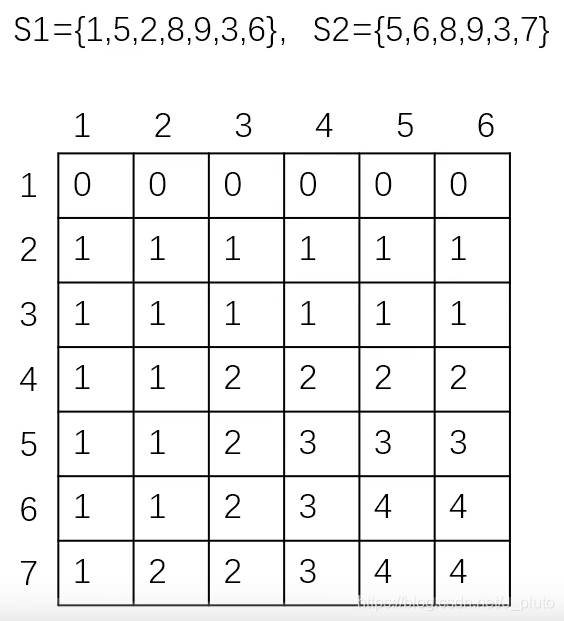
3.构造最优解
void LSC(int i,int j){
if(i==0||j=0)
return;
if(b[i][j]==1){
LCS(i-1,j-1);
cout<<S1[i]<<" ";
}
else if(b[i][j]==2)
LSC(i-1,j);
else
LSC(i,j-1);
}
下图为数组 b 的图解
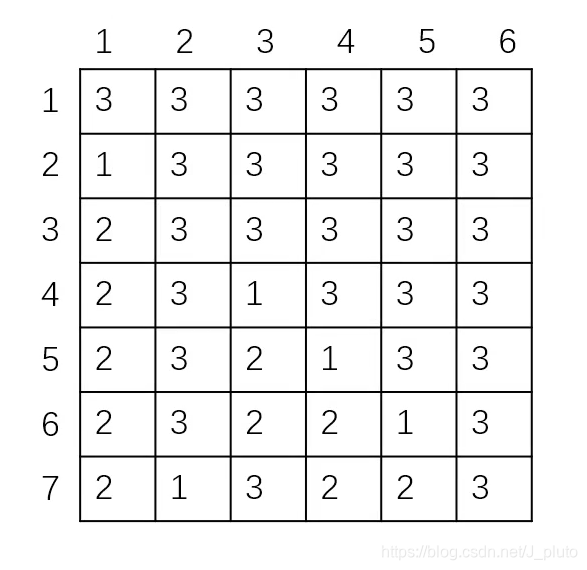
右下角开始,值为3时“←”,值为2时“↑”,值为1时“↖”,这样就找到了路径。返回时,如果 b[i][j]为1就输出。于是得到{5,8,9,3}。
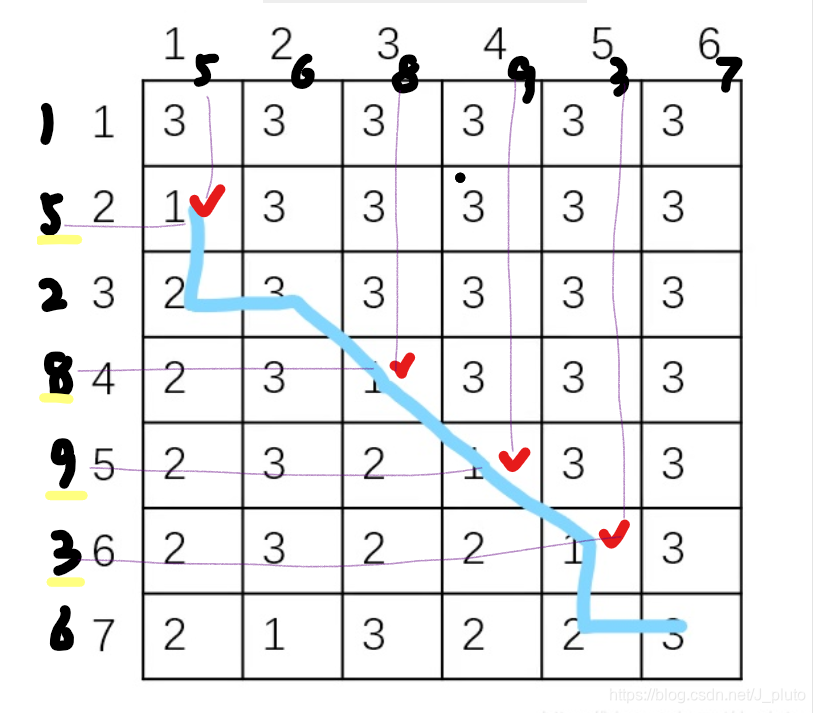




 本文详细解析了最长公共子序列(LCS)的概念,通过递推公式和动态规划方法,演示了如何求解两个序列的最长公共子序列。通过实例和代码展示了解决步骤,并介绍了如何构造最优解。
本文详细解析了最长公共子序列(LCS)的概念,通过递推公式和动态规划方法,演示了如何求解两个序列的最长公共子序列。通过实例和代码展示了解决步骤,并介绍了如何构造最优解。
















 621
621










