2021DAY5

---

最大子序列和问题

一、暴力解法

两层循环确定子列的左（i）右端（j）。第三层循环在左i右j内计算并更新子列和。这个算法遍历了所有子列，思路简单。但带来的一个弊处便是时间复杂度问题，不难算出O(n^3)。

代码如下：

int MaxSubseqSum1(int A[],int N){
	int ThisSum=0,MaxSum=0;
	int i,j,k;
	for(i=0;i<N;i++){          //i是子列左端的位置 
		for(j=i;j<N;j++){      //j是子列右端的位置 
			ThisSum=0;         //ThisSum是从A[i]到A[j] 的子列和 
			for(k=i;k<=j;k++){
				ThisSum+=A[k];
			}
			if(ThisSum>MaxSum){
				MaxSum=ThisSum;//更新最大子列和 
			} 
		}//j循环结束 
	}//i循环结束 
	return MaxSum; 
}

二、暴力进阶

此方法在第一种暴力的基础上稍加改进。我们在计算子列和时，可以通过累加方法，而不必再引入一层循环（k），这样做的一个目的便是可以降低时间复杂度。不难算出O(n^2)。

代码如下：

int MaxSubseqSum2(int A[],int N){
	int ThisSum=0,MaxSum=0;
	int i,j,k;
	for(i=0;i<N;i++){          //i是子列左端的位置 
		ThisSum=0; //ThisSum是从A[i]到A[j] 的子列和 
		for(j=i;j<N;j++){      //j是子列右端的位置      
			ThisSum+=A[j];//对于相同的i，不同的j，可以用累加完成 
			if(ThisSum>MaxSum){//如果得到的这个子列和更大 
				MaxSum=ThisSum;//更新最大子列和 
			} 
		}//j循环结束 
	}//i循环结束 
	return MaxSum; 
}

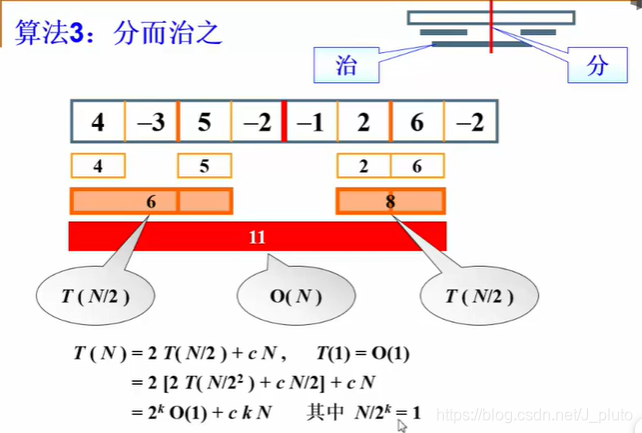
三、分而治之

此方法 通过二分及递归的思想实现。详细思路不赘述，放一张姥姥的网课图片。通常来说，如果有一个算法的时间复杂度为O(n^2)，我们一般会想办法将它降到O(nlogn)。

代码如下：

int Max3( int A, int B, int C )
{ /* 返回3个整数中的最大值 */
    return A > B ? A > C ? A : C : B > C ? B : C;
}
 
int DivideAndConquer( int List[], int left, int right )
{ /* 分治法求List[left]到List[right]的最大子列和 */
    int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */
    int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/
 
    int LeftBorderSum, RightBorderSum;
    int center, i;
 
    if( left == right )  { /* 递归的终止条件，子列只有1个数字 */
        if( List[left] > 0 )  return List[left];
        else return 0;
    }
 
    /* 下面是"分"的过程 */
    center = ( left + right ) / 2; /* 找到中分点 */
    /* 递归求得两边子列的最大和 */
    MaxLeftSum = DivideAndConquer( List, left, center );
    MaxRightSum = DivideAndConquer( List, center+1, right );
 
    /* 下面求跨分界线的最大子列和 */
    MaxLeftBorderSum = 0; LeftBorderSum = 0;
    for( i=center; i>=left; i-- ) { /* 从中线向左扫描 */
        LeftBorderSum += List[i];
        if( LeftBorderSum > MaxLeftBorderSum )
            MaxLeftBorderSum = LeftBorderSum;
    } /* 左边扫描结束 */
 
    MaxRightBorderSum = 0; RightBorderSum = 0;
    for( i=center+1; i<=right; i++ ) { /* 从中线向右扫描 */
        RightBorderSum += List[i];
        if( RightBorderSum > MaxRightBorderSum )
            MaxRightBorderSum = RightBorderSum;
    } /* 右边扫描结束 */
 
    /* 下面返回"治"的结果 */
    return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
 
int MaxSubseqSum3( int List[], int N )
{ /* 保持与前2种算法相同的函数接口 */
    return DivideAndConquer( List, 0, N-1 );
}

四、在线处理

只有一层循环，两个变量ThisSum（当前子列和），MaxSum（最大子列和）。每扫描一个元素，通过累加更新ThisSum，比较ThisSum和MaxSum，更新MaxSum；并作判断，如果ThisSum<0，则ThisSum=0，抛弃当新前子列，为负不可能使后面的部分和增大。
注意，这里比较容易误解成的是，判断当前元素为负，就抛弃。它并没有将之前计算的子列和都抛弃，前面算出的最大子列和已赋值给MaxSum。
这个算法的巧妙之处就是，在对每一个扫描进来的元素都是疑罪从无的原则，即使这个元素为负，使ThisSum减小，但这并不影响之后的元素再加进来使子列变大的可能性。而如果扫描进来的这个元素使ThisSum<0，就完全没有了使子列和增大的可能性，故将其弃之。
此算法为效率最高的，不难算出时间复杂度O(n)。之所以称之为解决最大子序列和问题的最高效算法，是因为，要想得到最长子列和，最基本的便是都要把每一个元素扫描一遍，而遍历每一个元素的时间复杂度为O(n)。

int MaxSubseqSum4(int A[],int N){
	int ThisSum,MaxSum;
	ThisSum=MaxSum=0;
	for(int i=0;i<N;i++){
		ThisSum+=A[i];
		if(ThisSum>MaxSum){
			MaxSum=ThisSum;
		}
		else if(ThisSum<0){//如果当前子列和为负 
			ThisSum=0;    //则不可能使后面的部分和增大，抛弃之 
		}
	}
	return MaxSum;
} 

---

cf

Lucky Sum of Digits
https://codeforces.com/problemset/problem/109/A

题目描述：将所给数，写成只有4，7组成的最小数字，若不能则输出-1。例如，11写为47，12写为444，10写为-1。

思路：把所给数拆成未知数个4，未知数个7，主要任务为统计4和7的个数。要保证最小，则先输出4，且7的个数尽量多。
注意：在保证7的个数尽量多时，要将第一层循环控制 写为4的个数。

#include<bits/stdc++.h>
using namespace std;
int n,i,j,k,flag;
int main()
{
	cin>>n;
	int s4,s7;
	s7=n/7;
	s4=n/4;
	for(i=0;i<=s4;i++){
		for(j=0;j<=s7;j++){
			if(n==i*4+j*7){
				flag=1;
				break;
			}
		}
		if(flag)
			break;
	}
	if(!flag)
		cout<<-1<<endl;
	else{
		for(k=1;k<=i;k++)
			cout<<"4";
		for(k=1;k<=j;k++)
			cout<<"7";
	}
	return 0;
}