数据结构 之 二叉树的概念（二）

提示：本篇章主要讲解数据结构中树的相关知识。

---

二叉树的定义

二叉树是n个结点的有限集，它或为空树(n=0)，或由一个根结点和两个分别称为左子树和右子树的互不相交的二叉树构成。
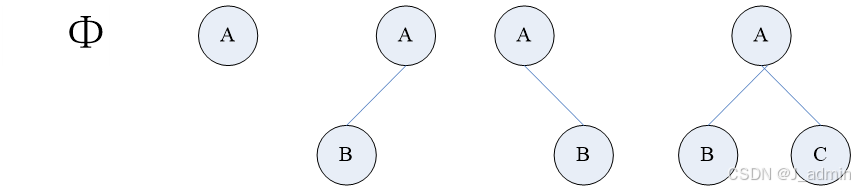分别是： 空二叉树、仅有根结点的二叉树、右子树为空的二叉树、左子树为空的二叉树，正常情况的二叉树

特别注意：一颗二叉树的度可以小于2

二叉树的性质

性质1：※ 在二叉树第i层上至多有２i-1 个结点（i≥1）。

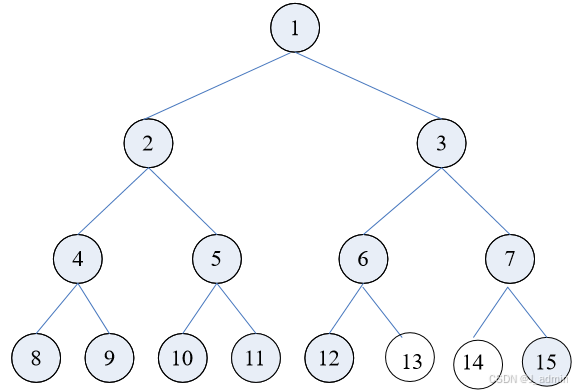
根据性质一：在一棵二叉树中，第5层上的结点数最多为16

性质2：※ 深度为k的二叉树至多有２k-1个结点，其中（k≥1）。

性质3：※ 在任意二叉树中，若叶子结点个数为n0，度为1的结点数为n1,度为2的结点数为n2 , 则n0 = n2 +1。
证明：设n代表二叉树中结点总数，所以，
n=n0+n1+n2 （公式1）

由于有n个结点的二叉树总分支数为n-1条，于是得：
n-1 = 0n0+1n1+ 2*n2 （公式2）

由公式1代入公式2可以得到 n0=n2+1

例如：若一棵二叉树具有10个度为2的结点，5个度为1的结点，则度为0的结点个数为（11）

满二叉树的概念

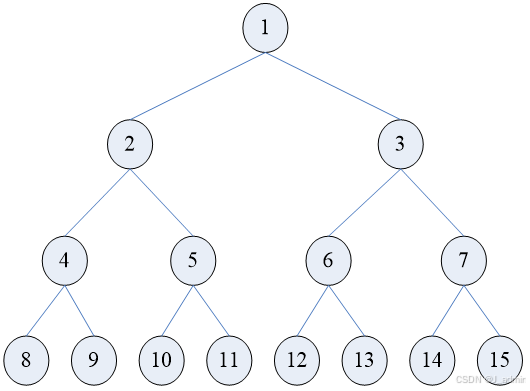
完全二叉树定义

深度为k,含有n个结点的二叉树，当且仅当其每个结点的编号与相应满二叉树及结点顺序编号从1~n相对应时，则称此二叉树为完全二叉树。

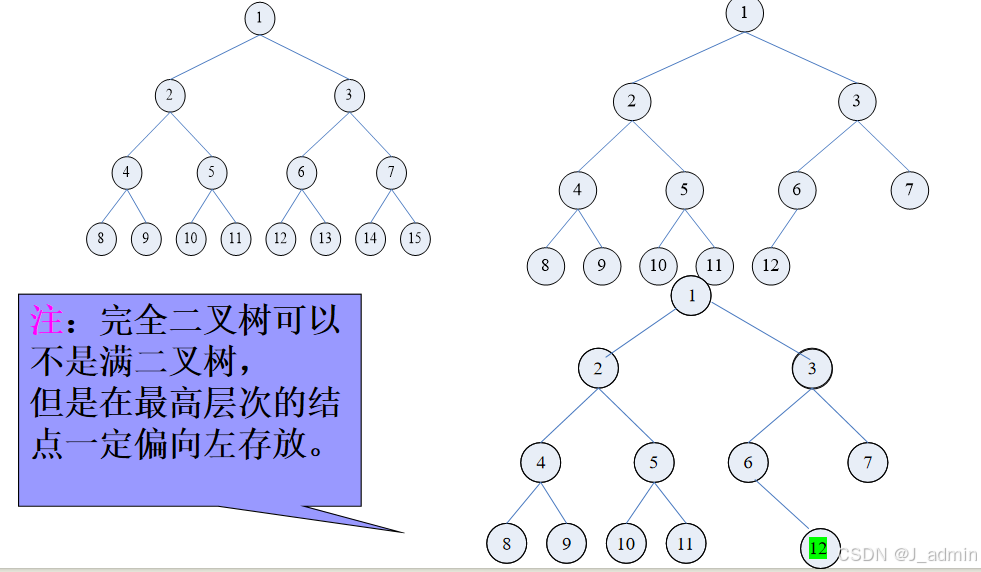
性质4：※ 具有n个结点的完全二叉树的深度为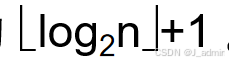

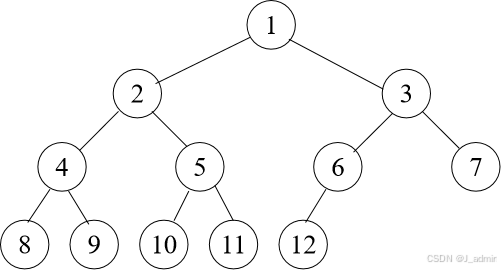
性质5：※ 如果对一棵有n个结点的完全二叉树的结点按层序编号，则对任一结点i（1≤i≤n)有：
(1) 如果i=1，则结点i是二叉树的根，无双亲；如果i>1，则其双亲是i/2；
(2) 如果2i>n，则结点i无左孩子；如果2i≤n，则其左孩子是2i；
(3) 如果2i+1>n，则结点i无右孩子；如果2i+1≤n，则其右孩子是2i+1。