强化学习 学习记录

基本概念

强化学习是做什么的：在于环境的交互中以最大化奖励函数为目的更新智能体的策略
与有监督学习的区别：在强化学习中无法获得大量即正确有具有代表性的训练数据
与无监督学习的区别：无监督学习目的是为了找到数据中的隐藏结构，而强化学习中找到隐藏结构不一定能使奖励函数最大，其最终目的还是获得最大奖励函数
最主要的区别：强化学习的训练数据是用于评估的而不是用于指导的

agent：一个具有交互能力，有具体目标的主体
enviroment:agent 的外部
policy：agent 在给定state的行动方式.
reward：完成一次交互后用于更新policy的值
value function：reward 的累加值
model：在学习过程中建立的对于环境的行为模型，推断模型的行为。带模型的方法叫model-based 方法，不带模型的叫model-free 方法。
state：包含environment完整信息的信号
observation：是对state的部分描述

Policy-Based Methods:通过告诉agent在具体状态下该采取什么行动，来训练policy。state会被映射为一个行动或是行动的概率分布.有两种形式：a）deterministic policy：在给定状态输出固定action b）stochastic policy：在给定状态输出的是执行各个action的概率，然后从中依照概率获得action
Value-Based Methods:让agent知道哪个state是更有价值的然后让agent采取行动往那个state行动，来训练一个value function。再根据value function选择行动

Off-policy:执行策略和更新参数用的策略不是相同策略（Q-learning）
On-policy:执行策略和更新参数用的策略是相同策略（SARSA）

强化学习中的一些问题

为什么要最大化奖励函数？

因为其中存在一个假设：所有目标可以被描述为最大化的奖励值

exploration and exploitation：exploitation 就是 进行目前观测到的能使奖励函数最大的操作 也称这种操作为 贪婪行动（greedy action），exploration 就是 放弃 greedy action 转而执行其他的一些行动，这样能观测到一些新的状态（可能有别的使奖励函数最大的行动）。简单来说exploitation就是关注短期收益，exploration就是关注长期收益。

Mulit-armed Bandits

bandit problem：只有单个state 的叫做老虎机问题
k-armed bandit problem：有k个臂（行动选择）的老虎机问题,每次执行行动会获得一个奖励，奖励数值遵从固定的概率分布（不知道如何分布的），目的是通过学习使奖励最大化。

行动的期望：
$$q_{\ast }(a)=E[R_t|A_t=a]$$
$A_t$是t时刻采取的行动，$R_t$是t时刻的奖励值，a是任意行动，$q_{\ast }(a)$是行动奖励期望 在这个问题中value 就是 行动奖励期望

解决方法

Action-value methods

根据估计行动的value，并且利用这些估计去行动的方法叫做 action-value methods
$$Q_t(a)=\frac{t时刻前采取行动a获得的奖励之和}{t时刻前采取行动a的次数}=\frac{{\sum }_{i=1}^{t-1}{R}_i\cdot 1_{A_i=a}}{{\sum }_{i=1}^{t-1}{1}_{A_i=a}}$$
$Q_t(a)$表示对于行动奖励期望的观察值 ，$1_{A_i=a}$表示当行动为a时取1否则取0。当分母为0时$Q_t(a)$设为一个默认值（在这里我们设为0），当分母为无穷大时，根据大数定理观测值趋于期望$q_{\ast }(a)$。

最简单的行动方法：greedy action： $A_t=argma{x}_a{Q}_t(a)$
greedy action 的缺点上面说过了

greedy action的改进方法：$\epsilon$-greedy method这个方法大部分时间都会采取greedy action 但是会有小的概率 $\epsilon$ 执行一个等概率选取所有行动的行动。
这个方法的好处在于：当行动的限制次数增加时能够使得所有$Q_t(a)$趋近于$q_{\ast }(a)$

利用两种算法执行10-armed testbed 可以看到在长期情况下$\epsilon$-greedy method 是比单纯的 greedy method 要好的多的。但这也需要根据情况来判断，由于10-armed testbed使用的是方差为1的正态分布，当方差变为10的时候，$\epsilon$-greedy method 需要花费更多steps来寻找最优行动，所以这种情况下反而还是greedy method好。

利用递增实现value的计算

计算某一行动的value： $Q_n=\frac{R_1+R_2+...+R_{n-1}}{n-1}$,$Q_n$代表这个行动被选择n-1此后的value观测值。
这个公式由于需要记住每个R和每个Q，所以会造成大量的资源消耗，为解决这个问题采用递增实现.
$$Q_{n+1}=\frac{1}{n}(\sum _1^n{R}_n)=\frac{1}{n}(R_n+\sum _1^{n-1}{R}_i)=\frac{1}{n}(R_n+(n-1)Q_n)=Q_n+\frac{1}{n}(R_n-Q_n)$$
这是个常见的形式
$$NewEstimate\leftarrow OldEstiamte+StepSize[Target-Oldestimate]$$

非静态问题

指的是奖励的概率随时间而变化，在这种情况下应该给value中晚测得的reward更大的权重，通过改变stepsize参数将其变为一个定值可以做到。

非静态情况下，stepsize = 1/n 情况下的bestaction率

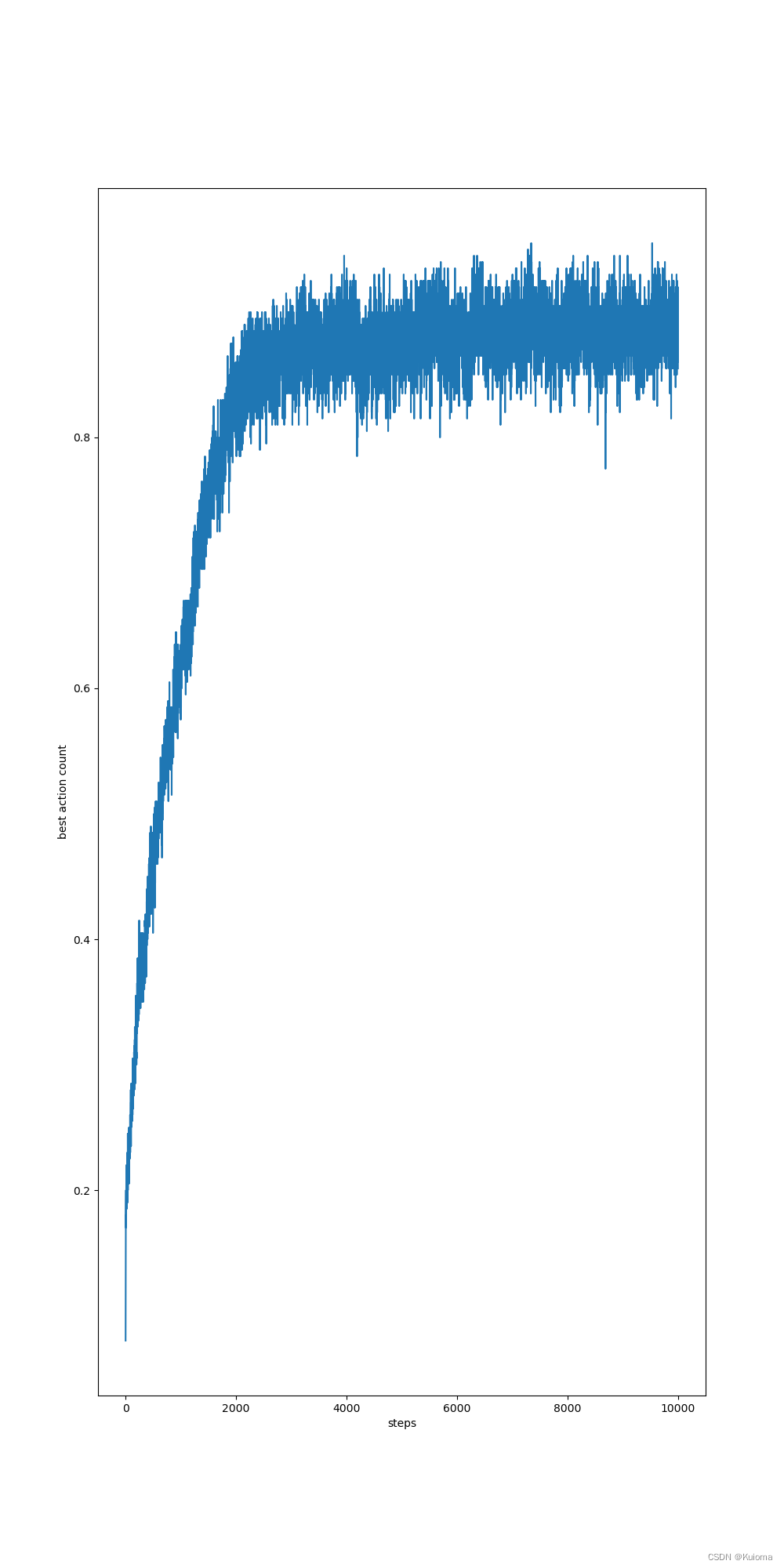
非静态情况下，stepsize = 0.1 情况下的bestaction率
可以看到在次数高的情况下stepsize为定值的准确率是高于1/n的情况的 ，这是由于当stepsize为1/n时行动会趋于稳定，而由于真实的value是非静态的也就是说最优行动是会改变的，这两者的矛盾导致了bestaction率的下降，改变stepsize参数可以解决这个问题

Optimistic Initial values

我们所讨论的这些方法在某种程度上都依赖于初始动作值的估计，当我们把初始值设置的高过实际value 很多时，这是一种鼓励探索的策略，因为当初始value设置的很高时无论接下来采取哪种行动都会感到不满意从而进行探索，这样就能保证所有的行动都能执行一定次数，即使实在greedyaction的情况下依旧能保证偏见的消除。但是这种对于初值设置的方法只对静态的情况下有效，因为他只能保证初期的探索。

Upper-Confidence-Bound Action Selection

UCB算法对于行动的选择是基于行动的不确定性，下面这个式子代表的是选择那些上置信限大的行动，也就是潜力大，不确定性大的行动
$$A_t=argma{x}_a[Q_t(a)+c\sqrt{\frac{lnt}{N_t(a)}}]$$
其中$N_t(a)$表示在t时刻前行动a被选取的次数，c表示置信程度。这个算法能够使得被选取次数少的行动跟多的被选择（t减少右边那项增加），使那些观测值低（左边那项小）的和频繁被选择（右边那项小）的更少的被选择。但是这个算法的使用范围没有$\epsilon$-greedy action大，尤其是在非静态条件下，使用这个算法仍然会使选择的行动收敛导致后期正确率降低。

Gradient bandit alogrithms

这个算法中行动的选择不再完全依赖于观测value的值，而是根据一个数字偏好（preference) $H_t$,赋予每个行动一个行动概率，一个行动偏好越大其执行行动的概率越大。具体概率根据softmax公式来获得。
$$Pr(A_t=a)=\frac{e^{Ht(a)}}{{\sum }_{k=1}^n{e}^{Ht(k)}}={\pi }_t(a)$$
每次行动执行完后每个行动的prefrence 会更新
$$H_{n+1}(a)=H_n(a)+\alpha (R_t-\overline{R_t})(1_{a=A_n}-{\pi }_n(a))$$
$1_{a=A_n}$表示当动作等于被选择的行动时它的值为1否则为0，$\overline{R_t}$表示不包含本次行动的reward平均值。直观来看这个式子表示当执行的行动奖励大于奖励均值时这个行动的偏好上升否则下降，同时其他行动的偏好会随着这个行动偏好的上升而下降，反之亦然。
这个式子其实是等价于梯度上升法的即：
$$H_{n+1}(a)=H_n(a)+\alpha \frac{dE(R_t)}{d{H}_n(a)}$$
其中$E(R_t)=\sum {\pi }_t(x)q^{\ast }(x)$,由于实际应用中$q^{\ast }$无法获得所以要通过一种能够采样得到的方法去逼近它
$$\begin{array}{r}\frac{dE(R_t)}{d{H}_n(a)}=\sum q^{\ast }(x)\frac{d{\pi }_t(x)}{d{H}_n(a)}=\sum (q\ast (x)-B_t(x))\frac{d{\pi }_t(x)}{d{H}_n(a)}\end{array}$$
这边等式能成立是因为概率对于偏好偏导的和为0，因为概率之和为零某行动偏好对于其行动概率的上升必然会导致其余行动概率的下降，反之亦然。
$$\begin{array}{rl}& =\sum {\pi }_t(x)(q\ast (x)-B_t(x))\frac{d{\pi }_t(x)}{d{H}_n(a)}\frac{1}{{\pi }_t(x)}\\ & =E[(q^{\ast }(A_t)-B_t(A_t))\frac{d{\pi }_t(A_t)}{d{H}_n(a)}\frac{1}{{\pi }_t(A_t)}]\end{array}$$
其中的$\frac{d{\pi }_t(x)}{d{H}_n(a)}$打开求导可以得到${\pi }_t(x)(1_{a=x}-{\pi }_t(a))$,直观来看这个式子就表示当action 等于 a时偏好的上升会使得对于这个行动选取概率的上升，而当action 不等于 a时 偏好的上升会导致其他行动选取概率的下降
$$=E[(R_t-\overline{R_t})(1_{a=A_t}-{\pi }_t(a))]$$
当t很大时根据大数定律取值等于期望然后带回，就能看出来这个方法是逼近梯度上升法的。