【Leetcode】28. 找出字符串中第一个匹配项的下标

KMP算法解析与实现

原创已于 2022-10-29 21:07:31 修改 · 827 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#1024程序员节

于 2022-10-24 15:49:08 首次发布

Leetcode 专栏收录该内容

6 篇文章

订阅专栏

一、Problem

Leetcode_28题目链接
给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例1：
输入：haystack = “sadbutsad”, needle = “sad”
输出：0
解释：“sad” 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

二、Prerequisites

参考-代码随想录
本题使用KMP算法解决，KMP算法是一种改进的字符串匹配算法，KMP的核心是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数从而达到快速匹配的目的。

KMP算法的核心在于构建一个前缀表，前缀表的长度与模式串的长度一致，前缀表中每个数字的含义为以当前位置的字符作为结尾字符时，其之前的最长相等前后缀的长度；
前缀就是：不包含主串最后一个字符的以主串第一个字符开头的所有连续字串；
后缀就是：不包含主串第一个字符的以主串最后一个字符结尾的所有连续字串；

考虑模式串="aabaaf"和主串=“aabaabaabfa”

模式串子串	前缀	后缀	最长公共前后缀长度	模式串当前下标
a	无	无	0	0
aa	a	a	1	1
aab	a,aa	b,ab	0	2
aaba	a,aa,aab	a,ba,aba	1	3
aabaa	a,aa,aab,aaba	a,aa,baa,abaa	2	4
aabaaf	a,aa,aab,aaba,aabaa	f,af,aaf,baaf,abaaf	0	5

可以看出模式串与前缀表对应位置的数字表示的是：下标i（包括i）的字符串中，有多大长度的相同前缀后缀
出现匹配失败的情况时，匹配失败的位置是在后缀子串的后面；此时通过前缀表记录的最长公共前后缀长度，可以知道最长相同的前缀和后缀，于是不用从头开始匹配模式串，而是回退到前缀后接着匹配就好了；
匹配失败后如何回到前缀后接着匹配？j=next[j-1]
生成前缀表即next数组的过程与使用前缀表进行匹配的过程其实是一致的，即生成前缀表的过程就是模式串自己与自己匹配的过程；这里实际上是一个错位匹配，因为next前缀表第一个元素一定是0，即其公共最长前后缀长度为0；那么就从下一位开始匹配，此时i指向后缀（以1起始），j指向前缀（以0起始）
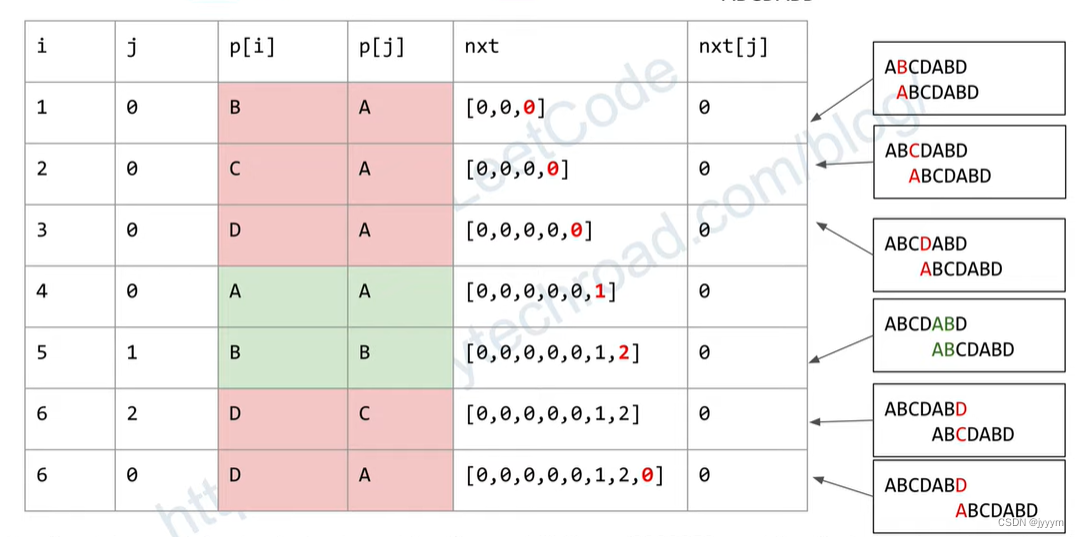
设主串长度为m，模式串长度为n，匹配时间复杂度为O(n)，生成前缀表的时间复杂度为O(m)，KMP算法的时间复杂度是O(m+n)；
使用KMP算法，构建前缀表即一个next数组是必须的。

三、Code

3.1 构建前缀表

即构建一个next数组，代码如下：

def getNext(s):
	# s为模式串
	# 使用j指向模式串前缀末尾，使用i指向模式串后缀末尾
	# 初始化next数组，注意到next数组第一个数字总是为0
	j = 0
	nextArr = [0] * len(s)
	nextArr[0] = j
	# i从1开始取值，遍历整个模式串
	for i in range(1, len(mode_string)):
		# 考虑当前缀和后缀不相同的情况
		# 肯定是当j>0时才开始比较
		while j>0 and s[i] != s[j]:
			j = nextArr[j-1]
		# 考虑前后缀相同的情况
		if s[i] == s[j]:
			j += 1
		nextArr[i] = j
	return nextArr

3.2 利用前缀表和主串进行匹配

代码如下：

class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        if len(needle) == 0:
            return 0

        nextArr = self.construct(needle)
        print(nextArr)
		# 开始进行匹配
		# j用于记录模式串起始位置
        j = 0
        # i用于记录主串的起使位置
        for i in range(len(haystack)):
        	# 不匹配的情况
        	# 回退到模式串前一个字符位置
            while j >0 and haystack[i] != needle[j]:
                j = nextArr[j-1]
            # 匹配的情况
            # 推进j
            if haystack[i] == needle[j]:
                j += 1
            # 当j指向模式串的末尾，表示匹配成功，返回位置信息
            if j == len(needle):
                return i - len(needle) + 1
        # 不匹配返回-1
        return -1
        
    def construct(self, needle):
        nextArr = [0] * len(needle)

        j = 0
        nextArr[0] = j

        for i in range(1, len(needle)):
            while j > 0 and needle[i] != needle[j]:
                j = nextArr[j-1]
            if needle[i] == needle[j]:
                j += 1
            nextArr[i] = j
        return nextArr