力扣随笔记-优快云博客

本文链接：https://blog.youkuaiyun.com/JDK8U231/article/details/144580332

Java中有双端队列（Deque）。Deque 接口是Java集合框架的一部分，它提供了双端队列的功能。双端队列允许元素从两端被插入和移除。Java提供了几种实现了Deque接口的类，其中最常用的是ArrayDeque和LinkedList。
java中栈的实现方式可以用List
Deque stack = new LinkedList();
stack.pop() stack.push() stack.isEmpty() stack.peek()

Queue是队列，
queue.poll() queue.offer() queue.isEmpty() queue.peek()

StringBulider
sb.delete(0,3), sb.insert(0,c), sb.append©
ASD
创建个Stack来储存右括号，遍历s时，每当遇见左括号就push一个相应的右括号。当遇见右括号时先判断stack是否为空，为空说明s中左括号少，false。如果stack不为空，说明左括号不少，再判断stack.pop的是不是该字符，不是则false（非正确顺序闭合）。遍历完之后，说明s中右括号都正确匹配到了左括号，消耗光了右括号，但不知道左括号还有没有剩余，此时再判断stack中是否为空，为空则左右正好，否则左多。（false情况：左少，左多，左右正好但非正确顺序）

Integer.parseInt(s)可以将字符串s解析为int。可以利用这个写出isNumber（）函数。

在这里插入图片描述
主要思想就是维护一个单调双端队列。这个队列储存窗口最大值的下标。
单调性的保证：每次要offerLast前，先判断nums[i]和nums[deque.peekLast()]的大小，直至nums[deque.peekLast()]大于nums[i]，再offerLast(i)
队列里只含窗口下标的保证：每次offerLast之后，循环比较deque.peekFirst()和窗口左端的下标值（i-k）,直至最大值下标在窗口内。

在这里插入图片描述
统计XX出现频率：HashMap
根据频率排序XX：优先级队列（PriorityQueue）的内部实现；绑定成[XX,频率]作为PriorityQueue的队员。
取出频率前K的XX：限制PriorityQueue容量为K。
PriorityQueue可以实现堆，默认为小顶堆。写个comparator来改为处理[XX,频率]的堆。在堆的K个成员里取最小值才能实现堆里留下K个最大值。
comparator.compare（）底层逻辑：当compare（）返回正值时，comparator认为左边的形参大于右边的形参。同理正负为小、平。所以只需在compare函数里运用左形参比较参数 - 右形参比较参数来return正负值即可。
Comparator只需要比较出两个形参大小就行，调用者再负责根据大小排序。

二叉树的迭代遍历模板：记住，模板的进栈顺序是根左。出栈顺序是左根。如果要前序，就在进栈时操作节点。中序则在出栈时操作节点。后序需要改模板，进栈顺序为根右，在进栈时《头插法》操作节点。

二叉树深度：递归。

二叉树直径：递归深度过程中，同时计算以该node为起点的路径，并与最大的进行比较。
此题需要知道的知识点：
1、任何一条路径都可由以某节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。（那么换句话说，遍历所有节点，并从每个节点出发，分别从其左儿子和右儿子向下遍历，可以得到所有可能的路径。）
2、一条路径的长度为该路径经过的节点数减一，所以要求路径长度就是求该路径上的节点数，那么就是求某个节点的左儿子和右儿子深度再+1.
所以在递归求深度的过程中计算出L和R后即可求某节点代表的路径节点数，递归过程中和全局变量ans对比留下最大的那个。最后不要忘记ans-1。
在这里插入图片描述
根据之前的知识点：任何一条路径都可由以某节点为起点，从其左儿子和右儿子向下遍历的路径拼接得到。（那么换句话说，遍历所有节点，并从每个节点出发，分别从其左儿子和右儿子向下遍历，可以得到所有可能的路径。）
我们只需要遍历所有节点，找到以每个节点为根节点（路径必包含根节点），分别向其左右儿子向下遍历即可。
那么我们需要写一个helper函数，输入root，返回经过root的路径的路径最大值（并且该路径可以和root的父节点组成新的路径）。
那么我们在递归过程中会有三个量来操作:left——经过左根的左树最大路径值,right——经过右根的右数最大路径值，root.val——根值。
怎么操作这三个量来返回经过根的当前树的最大路径值（并且该路径可和root父节点组成新路径）呢，我们先找到有哪些路径：只有根，左+根，右+根，左+右+根。但是左+右+根就不能再和其他父节点组成新路径了，所以helper返回时不能带上它，但是题目要求考虑所有路径，所以更新全局变量maxSum时需要考虑上。

验证二叉搜索树：中序遍历同时比较此节点值和上一节点值大小即可。
此题需要的知识点：二叉搜索树的中序遍历一定是升序的。

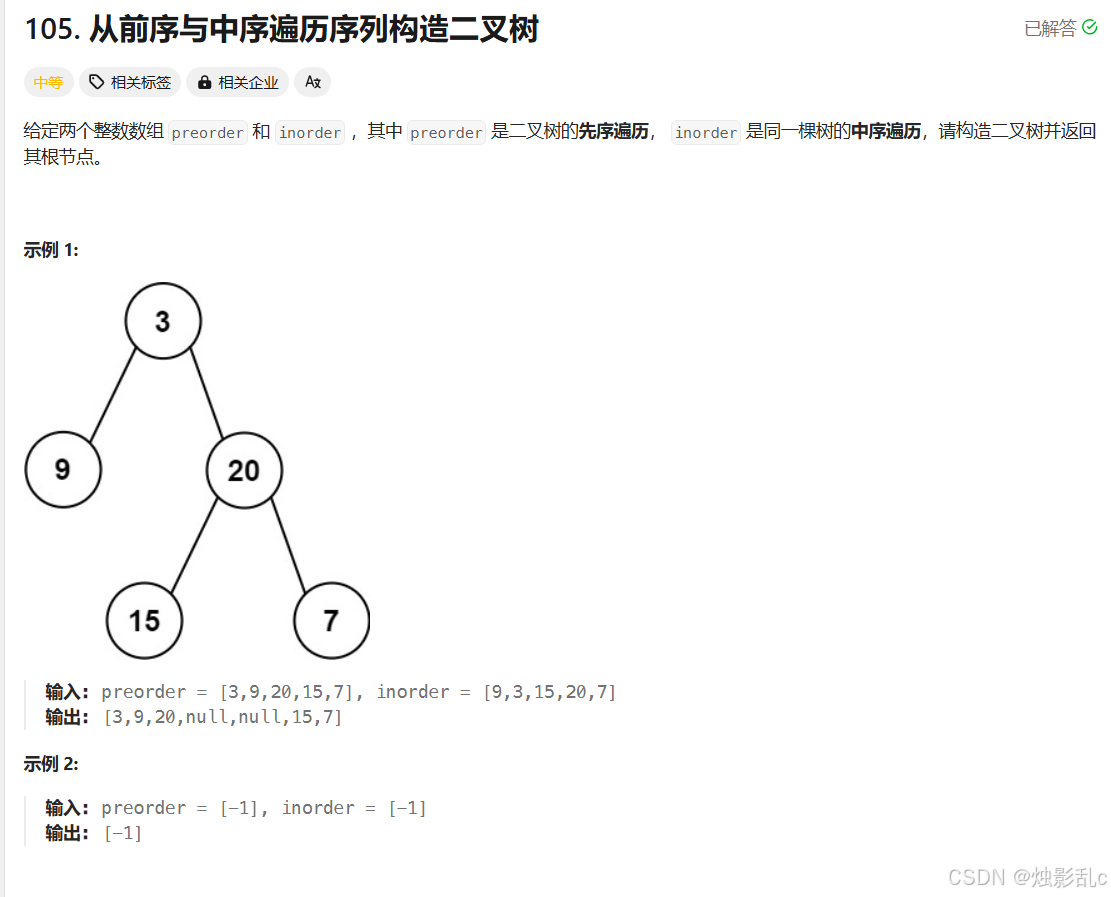
在这里插入图片描述
递归，递归函数helper作用：根据输入的preorder和inorder以及它们的start和end坐标，来构造该树。
helper的输入：整体的preorder和inorder，需要构建的子树的preorder的start和end；需要构建的子树的inorder的start和end。
helper的输出：构建好的子树的root节点。
递归出口：start > end；

递归逻辑：
找到根节点root。
root.left = helper(preorder,左子树preStart,左子树preEnd,inorder,左子树inStart,左子树inEnd).

所以关键的就是怎么用helper的输入preStart,preEnd,inStart,inEnd来求出左子树和右子树在preorder和inorder里的哪些start和end。这个在本上画图就行。
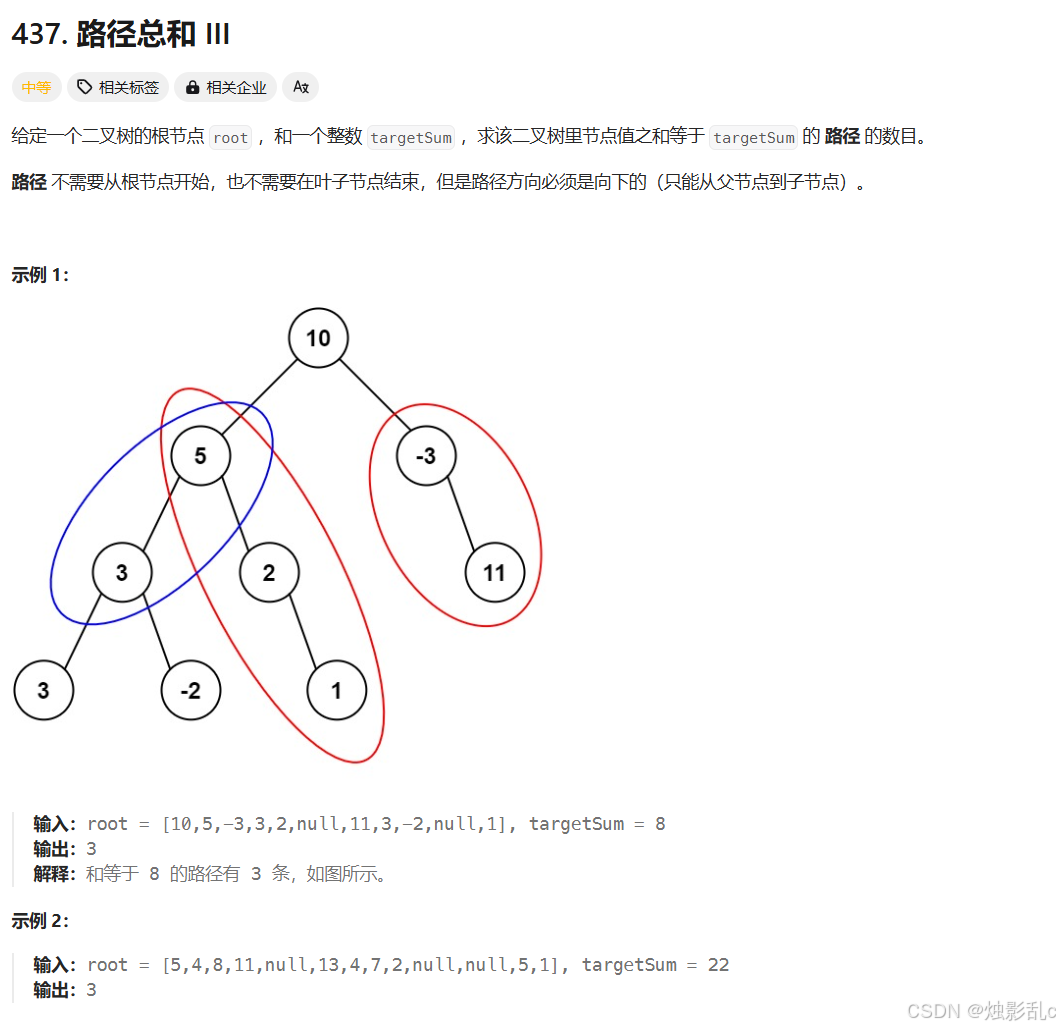
在这里插入图片描述
这道题给我的灵感就是，首先要搞清楚写的函数的功能。这个find函数的功能是：给你一棵树的根节点，返回以这棵树所有节点为起始点，构成的路径值为T的值。
搞清楚函数功能后，想想能不能使用这个函数递归一下。发现，如果能找到以root节点为起点，构成的路径值为T的值count，再加上find(左子，T)，和find（右子,T）就可以了。

所以问题转移到写找到以root节点为起点，构成的路径值为T的值，rootFind函数。一样，拿到一个函数首先考虑能不能递归使用它。如果rootFind(左子，T-root.val)，rootFind(右子，T-root.val)知道，直接++就行。最后注意如果root.val ==T，也是要++的。
所以解决。

在这里插入图片描述
下笔之前一定要搞清我们要写的函数的作用：找到root这棵树内pq的最近公共祖先，并返回这个公共祖先节点。

首先我们要知道关键信息，pq一定在root这棵树里。那么就有三种情况。
1、root为p或q时，另外一个在左或右子树中。此时root为最近公共祖先，
2、root不为p或q时。（1）pq不在同一侧，此时root为公共祖先。（2）pq在同一侧时。此时需判断pq在哪一侧，将在的那一侧再调用lowestCommonAncestor即可。

所以我们另写一个函数existPOrQ：如果root这棵树内存在p或q任意一个就返回true。

在这里插入图片描述
首先分割字串问题，画树时的第一层选择不一样！
以abcd为例，组合问题第一层如果i为1，就是从a开始，i=2就是从b开始。但是分割字符串，i =1,从a开始；i=2,是从ab开始！！不是从b开始。
还有个发现就是，for循环遵循：先选择(通过i来控制)，再判断(循环体内设置条件)。

在这里插入图片描述
每层去重的方法：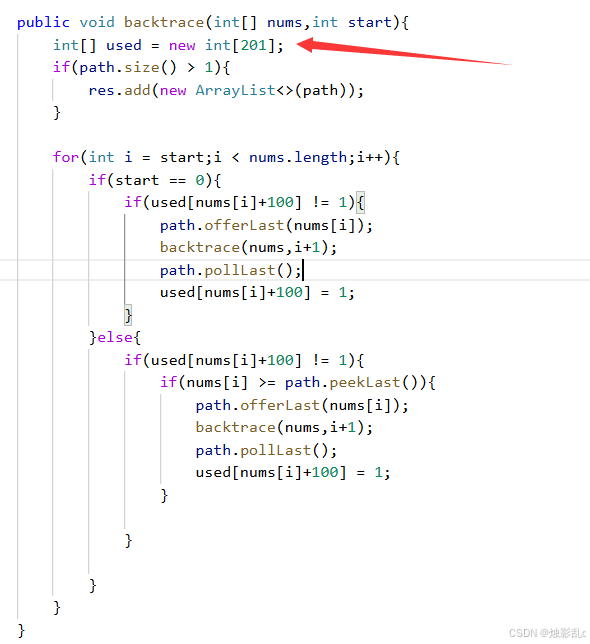
backtrace开头设置一个used数组，因为每一次backtrace就是一层。去重不仅要去除相邻两个数（用单变量last），还要去除不相邻（数组used）的两个数。
去重原因：第二个A能凑出来的情况，第一个A也能凑出来且比第二个多。如果同层再处理第二个A的话，res里面就有多余的path了。

同层去重：backtrace里面设置个int[] used数组。需要传入start，每次for循环从i = start开始。
同枝去重：设置个全局变量boolean[] used数组。不需要传入start，每次for循环从i = 0开始。

path加给res后，是否return是个很重要的点。如果需要进入下一层就不return;

回文子串的dp[i][j]定义！一定要围绕包括ij里的字串是否是回文（或最长子序列长度）。

黄金经验：先考虑递归，再dp，再技巧（如子数组和子串用前缀和。）

两数之和为target：哈希。

 class Solution {
    public int[] twoSum(int[] nums, int target) {
        Map<Integer,Integer> map = new HashMap<>();
        int[] res = new int[2];
        for(int i = 0;i < nums.length;i++){
            if(!map.containsKey(target - nums[i])){
                map.put(nums[i],i);
            }else{
                res[0] = i;
                res[1] = map.get(target - nums[i]);
                return res;
            }
        }
        return null;
    }   
}

异位词分组：哈希，key存排序后的词，value是list

class Solution {
    Map<String,List<String>> map = new HashMap<>();
    public List<List<String>> groupAnagrams(String[] strs) {
        for(String s:strs){
            char[] chs = s.toCharArray();
            Arrays.sort(chs);
            String sortchs = new String(chs);
            List<String> temp = map.getOrDefault(sortchs,new ArrayList<String>());
            temp.add(s);
            map.put(sortchs,temp);
        }
        List<List<String>> res = new ArrayList<>();
        for(Map.Entry<String,List<String>> e:map.entrySet()){
            res.add(e.getValue());
        }

        return res;
    }
    

}

最长连续序列：哈希set去重，找连续序列的最左数，找到则while循环至最右数同时max记录最大值

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> set = new HashSet<>();
        int res = 0;
        for(int n:nums){
            set.add(n);
        }
        for(int n:set){
            int temp = 0;
            if(!set.contains(n-1)){
                do{
                    temp++;
                    n++;
                }while(set.contains(n));
                res = Math.max(res,temp);
            }
        }
        return res;


    }
}

移动0：双指针，每次将快指针的值覆盖慢指针，快指针遇0则跳过再覆盖，直至尾部，慢指针再赋0.
盛水最多容器：头尾双指针，移动矮端。
三数之和为0：排序，遍历时双指针，从头开始遍历，确定第一个数后，头尾双指针。注意sum==0时，n[L] == n[L+1]时需L++。

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(nums);
        for(int i= 0;i < nums.length-2;i++){
            if(i >0 && nums[i] == nums[i-1]){
                continue;
            }
            if(nums[i] > 0){
                break;
            }
            
            for(int m = i+1,n = nums.length -1;m < n;){
                if(nums[i] + nums[m] + nums[n] == 0){
                    List<Integer> path = new ArrayList<>();
                    path.add(nums[i]);
                    path.add(nums[m]);
                    path.add(nums[n]);
                    res.add(path);
                    while(m < n && nums[m+1] == nums[m]){
                        m++;
                    }
                    while(m < n && nums[n-1] == nums[n]){
                        n--;
                    }
                    m++;
                    n--;
                }else{
                    if(nums[i] + nums[m] + nums[n] > 0){
                        n--;
                    }else{
                        m++;
                    }
                }
            }
        }
        return res;
    }
}

无重复字符的最长子串：双指针，set存储子串字符，ml，mr标记答案子串的左右下标。当重复时，l–至不重复。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        if(s.length() == 0){
            return 0;
        }
        Set<Character> set = new HashSet<>();
        int ml=0,mr=1;
        int left = 0,right = 1;
        set.add(s.charAt(0));
        while(right < s.length()){
            if(!set.contains(s.charAt(right))){
                set.add(s.charAt(right));
                right++;
            }else{
                while(left<right && set.contains(s.charAt(right))){
                    set.remove(s.charAt(left));
                    left++;
                }
                set.add(s.charAt(right));
                right++; 
            }
            if(right - left > mr - ml){
                ml = left;
                mr = right;
            }
        }

        return mr - ml;


    }
}

找到字符串中所有字母异位词返回子串首字母下标：滑动窗口，从p中找q，用两个int[128]存字符出现次数，Arrays.equal比较是否相同。从p开始滑，滑出的字符在int[]里–，滑入的++，再equal。

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        if(s.length() < p.length()){
            return new ArrayList<>();
        }
        List<Integer> res = new ArrayList<>();
        int[] have = new int[128];
        int[] need = new int[128];
        for(char c:p.toCharArray()){
            need[c]++; 
        }
        for(int i = 0;i < p.length();i++){
            have[s.charAt(i)]++;
        }
        if(Arrays.equals(have,need)){
            res.add(0);
        }
        for(int i = p.length();i < s.length();i++){
            have[s.charAt(i)]++;
            have[s.charAt(i-p.length())]--;
            if(Arrays.equals(have,need)){
                res.add(i - p.length()+1);
            }
            
        }
        return res;
        
    }
}

和为 K 的子数组个数：前缀和。
滑动窗口最大值：递减队列存下标。从队尾入队，直至前面是比它大的。每次滑动后判断队头是否滑出，滑出则删除队头。判断后再peek队头。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        Deque<Integer> deque = new LinkedList<>();
        int[] res = new int[nums.length - k +1];
        for(int i = 0;i <k;i++){
            while(!deque.isEmpty()&&nums[deque.peekLast()]<= nums[i]){
                deque.pollLast();
            }
            deque.offerLast(i);
        }
        res[0] = nums[deque.peekFirst()];
        for(int i = k;i <nums.length;i++){
            while(!deque.isEmpty()&&nums[deque.peekLast()] <= nums[i]){
                deque.pollLast();
            }
            if(!deque.isEmpty()&&deque.peekFirst()<=i-k){
                deque.pollFirst();
            }
            deque.offerLast(i);
            res[i-k+1] = nums[deque.peekFirst()];
        }
        return res;
        
    }
}

最小覆盖子串：从s中找覆盖t字符的最小子串，快慢指针，两个int[] need和have存放出现字符次数，count记录子串已有符合字符数，当count==tl时说明该子串符合，ml和mr记录该次下标，移动左界限，while循环至count != tl。当r的字符在need中且need >= have时count++。

class Solution {
    public String minWindow(String s, String t) {
        int sl = s.length(),tl = t.length();
        if(sl < tl ){
            return "";
        }
        int[] needs = new int[100];
        int[] have = new int[100];
        String res = "";
        for(char c:t.toCharArray()){
            needs[c - 'A']++;
        }
        int left = 0,right = 0,minLength = sl+1,count=0;
        while(right < sl){
            char c = s.charAt(right);
            have[c - 'A']++;
            if(needs[c - 'A']>0&&needs[c-'A'] >= have[c - 'A']){
                count++;
            }
            while(count == tl){
                char lc = s.charAt(left);
                if(right - left +1 < minLength){
                    minLength = right - left +1;
                    res=s.substring(left,right+1);
                }
                if(needs[lc - 'A']>0&&needs[lc - 'A']==have[lc - 'A']){
                    count--;
                }
                have[lc - 'A']--;
                left++;
            }
            right++;
        }
        return res;
        

    }
}

最大子数组和:dp
合并区间：Arrays.sort时用Comparator的compare排序左端点。遍历数组，比较当前区间左端点与集合内最后区间右端点，当>时，当前区间直接加入集合；<=时，更新记录的右端点即可。

class Solution {
    public int[][] merge(int[][] intervals) {
        List<int[]> temp = new ArrayList<>();
        Arrays.sort(intervals,new Comparator<int[]>(){
            public int compare(int[] interval1,int[] interval2){
                return interval1[0] - interval2[0];
            }
        });
        
        int left = intervals[0][0],right = intervals[0][1];
        for(int i = 1;i < intervals.length;i++){
            if(intervals[i][0] <= right){
                right = Math.max(right,intervals[i][1]);
            }else{
                temp.add(new int[]{left,right});
                left = intervals[i][0];
                right = intervals[i][1];
            }
        }
        temp.add(new int[]{left,right});
        return temp.toArray(new int[temp.size()][]);
    }
}

轮转数组：分段反转再整体反转。
除自身以外数组的乘积:两个数组存左和右的乘积，第一次遍历填充左右数组，第二次遍历填充res。
缺失的第一个正整数：理想的数组12-345，可以看出返回的是异常下标+1，所以我们目的就是怎么把输入数组转成理想数组，然后再遍历理想数组即可。从前往后遍历，当num[i] > 0 && <= length && num[i] != num[nums[i] - 1]。

class Solution {
    public int firstMissingPositive(int[] nums) {
        //众神归位法
        int res = 0;
        int nl = nums.length;
        
        while(res < nl){
            if(nums[res] == res + 1){
                res++;
            }else{
                if(nums[res] > nl || nums[res] < res + 1||nums[nums[res] - 1] == nums[res]){
                    nums[res] = nums[nl - 1];
                    nl--;
                }else{
                    int temp = nums[res];
                    nums[res] = nums[temp - 1];
                    nums[temp - 1] = temp;
                }
            }
        }
        return res+1;

    }
}

如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0：boolean[m]和boolean[n]，遍历矩阵当遇0则对应boolean置true。再遍历m,n。
螺旋矩阵：模拟，四个指针，lt，rt,lb,rb。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        List<Integer> res = new ArrayList<>();
        int l = 0,r = matrix[0].length-1;
        int t = 0,b = matrix.length-1;
        while(l <=r && t <= b){
            for(int i = l;i <= r&&t <= b;i++){
                res.add(matrix[t][i]);
            }
            t++;
            for(int i = t;i <= b&&l <= r;i++){
                res.add(matrix[i][r]);
            }
            r--;
            for(int i = r;i >=l&&t <= b;i--){
                res.add(matrix[b][i]);
            }
            b--;
            for(int i = b;i >= t&&l <= r;i--){
                res.add(matrix[i][l]);
            }
            l++;
        }
        return res;
        

        
    }
}

旋转图像：先水平翻转，再主对角线。

class Solution {
    public void rotate(int[][] matrix) {
        int temp;
        for(int i = 0;i < matrix.length ;i++){
            for(int j = 0 ;j < matrix.length ;j++){
                if(matrix.length - 1 -i > i){
                    temp = matrix[i][j];
                    matrix[i][j] = matrix[matrix.length - 1 - i][j];
                    matrix[matrix.length - 1 - i][j] = temp;
                }
            }
        }
        for(int i = 0;i < matrix.length - 1;i++ ){
            for(int j = i + 1;j < matrix.length;j++){
                temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        
    }

    
}

搜索有序矩阵：右上角开始，要么行++，要么列–。
相交链表：每次向前走，遇null则重置到另个链表头节点，直至A == B。
反转链表：递归
判断回文链表：翻转后半部分再遍历比较。
环形链表：快慢指针，快走两步，慢走一步，相遇反true。如果需环入口，相遇快重置至head，同走一步，直至相遇。
合并两个有序链表：新建res指向最小节点，temp指向结果链表的尾节点，将temp.next指向两者最小，直至list1为null或者list2为null。再把temp.next指向非null。递归更简单，找到最小值再用递归即可。

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
        if(list1 == null && list2 == null){
            return null;
        }
        if(list1 == null && list2 != null){
            return list2;
        }
        if(list2 == null && list1 != null){
            return list1;
        }
        
        ListNode temp;
        if(list1.val <= list2.val){
                temp = list1;
                list1 = list1.next;
                
            }else{
                temp = list2;
                list2 = list2.next;
            }
        ListNode res = temp;
        while(list1 != null && list2!= null){
            if(list1.val <= list2.val){
                temp.next = list1;
                list1 = list1.next;
                
            }else{
                temp.next = list2;
                list2 = list2.next;
            }
            temp = temp.next;
        }
        ListNode list = list1 == null?list2:list1;
        temp.next = list;
        return res;
    }
}

逆序链表两数相加：新建res指向开头，temp指向尾节点，carrier表示进数，当l1 != null或 l2!= null或 carrier != 0时都进入循环算sum，然后利用sum新建节点接入temp，更新carrier，l1 l2更新

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        
        ListNode res = new ListNode();
        ListNode temp = res;
        int carrier = 0;
        while(l1 != null || l2 != null || carrier != 0){
            int sum = (l1 == null?0:l1.val) + (l2 == null?0:l2.val) +carrier;

            temp.next = new ListNode(sum % 10);
            temp = temp.next;
            carrier = sum / 10;

            if(l1 != null){
                l1 = l1.next;
            }
            if(l2 != null){
                l2 = l2.next;
            }
        }

        return res.next;
    }
}

删除链表倒数第N个节点：新建res指向开头，使正常删除头节点，再快慢指针。
两两交换链表中的节点：递归

class Solution {
    public ListNode swapPairs(ListNode head) {
        return change(head);
    }
    public ListNode change(ListNode node){
        if(node == null){
            return null;
        }
        if(node.next == null){
            return node;
        }
        ListNode res = node.next;
        node.next = change(node.next.next);
        res.next = node;
        
        return res;
    }
}

K 个一组翻转链表：运用reverse翻转链表函数，新建res节点为前驱节点，pre也为前驱节点，遍历end到小链表最后一个元素，提前标记下个小链表开头，以便pre过去。

public ListNode reverseKGroup(ListNode head, int k) {
    ListNode dummy = new ListNode(0);
    dummy.next = head;

    ListNode pre = dummy;
    ListNode end = dummy;

    while (end.next != null) {
        for (int i = 0; i < k && end != null; i++) end = end.next;
        if (end == null) break;
        ListNode start = pre.next;
        ListNode next = end.next;
        end.next = null;
        pre.next = reverse(start);
        start.next = next;
        pre = start;

        end = pre;
    }
    return dummy.next;
}

private ListNode reverse(ListNode head) {
    ListNode pre = null;
    ListNode curr = head;
    while (curr != null) {
        ListNode next = curr.next;
        curr.next = pre;
        pre = curr;
        curr = next;
    }
    return pre;
}

排序链表：递归+归并排序。

class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null){
            return null;
        }
        if(head.next == null){
            return head;
        }
        ListNode res = new ListNode();
        res.next = head;
        ListNode slow = res,quick = res;
        
        while(quick.next != null){
            quick = quick.next;
            if(quick.next != null){
                quick= quick.next;
            }
            slow = slow.next;
        }
        ListNode next = slow.next;
        slow.next = null;
        ListNode left = sortList(res.next);
        ListNode right = sortList(next);
        
        return merge(left,right);

    }

    public ListNode merge(ListNode left,ListNode right){
        ListNode res = new ListNode();
        ListNode ress = res;
        while(left!=null && right != null){
            if(left.val <= right.val){
                ress.next = new ListNode(left.val);
                
                left = left.next;
            }else{
                ress.next = new ListNode(right.val);
                right = right.next;
            }
            ress = ress.next;

        }
        ListNode temp = left == null?right:left;
        ress.next = temp;
        return res.next;
        
    }
    
}

合并 K 个升序链表：多次运用合并两个升序链表函数。

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if(lists == null){
            return null;
        }

        Set<ListNode> picked = new HashSet<>();
        List<ListNode> listhead = new ArrayList<>();

        for(ListNode n:lists){
            if(picked.contains(n)){
                continue;
            }
            if(n == null){
                continue;
            }else{
                listhead.add(n);
                while(n.next != null){
                    n = n.next;
                    picked.add(n);
                }
            }
        }
        if(listhead.isEmpty()){
            return null;
        }
        if(listhead.size() == 1){
            return listhead.get(0);
        }
        ListNode res = new ListNode();
        res.next = merge(listhead.get(0),listhead.get(1));
        for(int i = 2;i < listhead.size();i++){
            res.next = merge(res.next,listhead.get(i));
        }
        return res.next;

        
        
    }

    public ListNode merge(ListNode left,ListNode right){
        ListNode res = new ListNode();
        ListNode ress = res;
        while(left!=null && right != null){
            if(left.val <= right.val){
                ress.next = new ListNode(left.val);
                
                left = left.next;
            }else{
                ress.next = new ListNode(right.val);
                right = right.next;
            }
            ress = ress.next;

        }
        ListNode temp = left == null?right:left;
        ress.next = temp;
        return res.next;
        
    }
}

LRU缓存：使用Node<key,val>存放元素，并且Node类里有next和pre指针，也就是说使用双向链表记录优先级；使用hashset记录是否存在此Key。用head和tail记录头尾。当刚put或访问时，将key对应node移到队尾。

class Node{
    int key;
    int value;
    Node next;
    Node pre;
    public Node(){};
    public Node(int key,int value){
        this.key = key;
        this.value = value;
    }
}
class LRUCache {
    Map<Integer,Node> map = new HashMap<>();
    int capacity;
    Node first = new Node();
    Node last = new Node();
    public LRUCache(int capacity) {
       this.capacity = capacity;
       first.next = last;
       last.pre = first;
    }
    
    public int get(int key) {
        Node temp = map.getOrDefault(key,null);
        if(null == temp){
            return -1;
        }else{
            temp.pre.next = temp.next;
            temp.next.pre = temp.pre;
            temp.pre = last.pre;
            temp.next = last;
            last.pre.next = temp;
            last.pre = temp;
            return temp.value;
        }
    }
    
    public void put(int key, int value) {
        Node temp = map.getOrDefault(key,null);
        if(null == temp){
            temp = new Node(key,value);
            map.put(key,temp);
            temp.next = last;
            temp.pre = last.pre;
            last.pre.next = temp;
            last.pre = temp;
        }else{
            temp.value = value;
            temp.pre.next = temp.next;
            temp.next.pre = temp.pre;
            temp.pre = last.pre;
            temp.next = last;
            last.pre.next = temp;
            last.pre = temp;
        }
        
        if(map.size() > capacity){
            map.remove(first.next.key);
            first.next.next.pre = first;
            first.next = first.next.next;
        }
    }
}

二叉树中序，前序：模板。

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        
        while(root != null){
            stack.offerLast(root);
            root = root.left;
        }

        while(!stack.isEmpty()){
            TreeNode n = stack.pollLast();
            res.add(n.val);
            TreeNode r = n.right;
            while(r != null){
                stack.offerLast(r);
                r = r.left;
            }
        }
        return res;
    }
    
}

二叉树后序：将根左变为根右。入栈时头插。

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        while(root != null){
            stack.offerLast(root);
            res.add(0,root.val);
            root = root.right;
        }
        while(!stack.isEmpty()){
            TreeNode n = stack.pollLast();
            TreeNode l = n.left;
            while(l != null){
                stack.offerLast(l);
                res.add(0,l.val);
                l = l.right;
            }
        }
        return res;
    }
}

二叉树最大深度：队列，层序遍历。
翻转二叉树：递归

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        invertTree(root.left);
        invertTree(root.right);
        TreeNode l = root.left;
        root.left = root.right;
        root.right = l;
        return root;
    }
    

    
    

}

判断对称二叉树：递归，新建函数hlper为判断left和right是否对称。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return dfs(root.left,root.right);

    
    }
    
    public boolean dfs(TreeNode left,TreeNode right){
        if(left == null && right == null){
            return true;
        }
        if(left == null || right == null){
            return false;
        }
        if(left.val != right.val){
            return false;
        }
        
        return dfs(left.left,right.right)&&dfs(left.right,right.left);
    }
    
}

树中任意两个节点之间最长路径的长度：新建函数判断节点最长半边路径。过程中用res记录最长双边长度。

class Solution {
    int ans;
    public int diameterOfBinaryTree(TreeNode root) {
        
        ans = 1;
        depth(root);
        return ans -1;
    }

    public int depth(TreeNode node){
        if(node == null){
            return 0;
        }
        int L = depth(node.left);
        int R = depth(node.right);
        ans = Math.max(ans,L+R+1);
        return Math.max(L,R)+1;
    }
}

将有序数组转换为二叉搜索树：新建hlepr传入数组和左右下标递归构建二叉搜索树。

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return helper(nums,0,nums.length-1);
    }
    public TreeNode helper(int[] nums,int left,int right){
        if(left > right){
            return null;
        }
        int mid = (left + right)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = helper(nums,left,mid-1);
        root.right = helper(nums,mid+1,right);
        return root;
    }
}

验证二叉搜索树：二叉搜索树的中序遍历是升序的。
路径总和为t：递归,结果为this(root.left,t)+this(root.right,t)+helper(root,t)，其中helper是求必包括root时的路径数量，helper也是递归

class Solution {

    public int pathSum(TreeNode root, int targetSum) {
        if(root == null){
            return 0;
        }
       return helper(root,targetSum)+pathSum(root.left,targetSum)+pathSum(root.right,targetSum);
    }

    public int helper(TreeNode root,long target){
        if(root == null){
            return 0;
        }
        int count = 0;
        if(root.val == target){
            count = 1;
        }
        int left = helper(root.left,target - root.val);
        int right = helper(root.right,target - root.val);
        
        return left + right+count;
    }
    
}

二叉树公共祖先：hleper为监测某节点是否在当前树中。如果p与q都在root.left中，则return this(root.left)。如果pq不在同一子树中，return root。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
       if(root == p ||root == q){
        return root;
       }
       if(existPOrQ(root.left,p,q)&&existPOrQ(root.right,p,q)){
        return root;
       }
       if(existPOrQ(root.left,p,q)){
        return lowestCommonAncestor(root.left,p,q);
       }else{
        return lowestCommonAncestor(root.right,p,q);
       }
       
    }

    public boolean existPOrQ(TreeNode root,TreeNode p,TreeNode q){
        if(root == null){
            return false;
        }
        if(root.val == p.val || root.val == q.val){
            return true;
        }
        return existPOrQ(root.left,p,q) || existPOrQ(root.right,p,q);
    }

    

}

最大路径和：路径可以对折，那么求每个节点的最大路径和，同时取max即可。helper求包括root时最大的边路径和。那么root的最大路径和就三种情况：只有自己，自己+helper（root.left），自己+helper（root.right）.

class Solution {
    int res = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
       helper(root);
       return res;
    }
    public int helper(TreeNode root){
        if(root == null){
            return 0;
        }
        int left = helper(root.left);
        int right = helper(root.right);
        int max = Math.max(Math.max(left,right)+root.val,root.val);
        int maxpath = Math.max(root.val,Math.max(root.val+left,Math.max(root.val+right,root.val+left+right)));
        res = Math.max(res,maxpath);
        return max;
    }
    
}

岛屿数量：给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。

class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int i = 0; i < grid.length; i++) {
            for(int j = 0; j < grid[0].length; j++) {
                if(grid[i][j] == '1'){
                    dfs(grid, i, j);
                    count++;
                }
            }
        }
        return count;
    }
    private void dfs(char[][] grid, int i, int j){
        if(i < 0 || j < 0 || i >= grid.length || j >= grid[0].length || grid[i][j] == '0') return;
        grid[i][j] = '0';
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);
    }
}

N皇后：

class Solution {
    List<List<String>> res = new ArrayList<>();
    Deque<String> path = new LinkedList<>();
    boolean[][] used;
    public List<List<String>> solveNQueens(int n) {
       used =new boolean[n][n];
       backtrace(n,0);
       return res;
    }

    public void backtrace(int n,int row){
        if(row == n){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = 0;i < n;i++){
            if(check(row,i,n)){
                path.offerLast(makePath(n,i));
                used[row][i]= true;
                backtrace(n,row+1);
                used[row][i] = false;
                path.pollLast();
            }
        }
    }

    public boolean check(int m,int n,int max){
        for(int i = m;i >=0;i--){
            if(used[i][n]){
                return false;
            }
        }
        for(int i = m,j = n;i >=0&&j>=0;i--,j--){
            if(used[i][j]){
                return false;
            }
        }
        for(int i = m,j = n;i >=0&&j<max;i--,j++){
            if(used[i][j]){
                return false;
            }
        }
        return true;
    }

    public String makePath(int n,int j){
        StringBuilder sb = new StringBuilder();
        for(int i = 0;i < n;i++){
            if(i != j){
                sb.append('.');
            }else{
                sb.append('Q');
            }
        }
        return sb.toString();
    }
    
    
}

分割回文子串：

class Solution {
    List<List<String>> res = new ArrayList<>();

    Deque<String> path = new LinkedList<>();
    public List<List<String>> partition(String s) {
       backtrace(s.toCharArray(),0);
       return res;
    }

    public void backtrace(char[] chars,int start){
        if(start == chars.length){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = start;i < chars.length;i++){
            if(check(chars,start,i)){
                path.offerLast(new String(chars,start,i - start +1));
                backtrace(chars,i+1);
                path.pollLast();
            }
        }
    }

    public boolean check(char[] chars,int start,int end){
        while(end >= start){
            if(chars[start++] != chars[end--]){
                return false;
            }
        }
        return true;
    }

   
}

单词搜索：

class Solution {
    Deque<Character> path = new LinkedList<>();
    boolean[][] usedZ;
    
    public boolean exist(char[][] board, String word) {
        int res;
        usedZ = new boolean[board.length][board[0].length];
        for(int i = 0;i < board.length;i++){
            for(int j = 0;j < board[0].length;j++){
                if(backtrace(board,word.toCharArray(),i,j,0)){
                    return true;
                }
            }
        }
        return false;
    }
    public boolean backtrace(char[][] board,char[] word,int m,int n,int index){
       if(index == word.length){
            return true;
       }

       if(m <0 || m >= board.length || n < 0||n >= board[0].length||usedZ[m][n] || board[m][n] != word[index]){
        return false;
       }
       usedZ[m][n] = true;
       boolean res = backtrace(board,word,m,n+1,index+1)||
                    backtrace(board,word,m+1,n,index+1)||
                    backtrace(board,word,m,n-1,index+1)||
                    backtrace(board,word,m-1,n,index+1);

        usedZ[m][n] = false;
        return res;
    }
    public boolean check(Deque<Character> path,char[] word){
        int i =0;
        for(char c:path){
            if(c != word[i]){
                return false;
            }
            i++;
        }
        return true;
    }
}

n对括号可生成的所有有效组合：

class Solution {
    List<String> res = new ArrayList<>();
    Deque<Character> path = new LinkedList<>();
    int[] used = new int[2];
    public List<String> generateParenthesis(int n) {
       backtrace(n);
       return res;
    }
    public void backtrace(int n){
        if(path.size() == 2*n){
            if(helper(path)){
                StringBuilder sb = new StringBuilder();
                for(char c:path){
                    sb.append(c);
                }
                res.add(sb.toString());
            }
            return;
        }

        for(int i = 0;i <used.length;i++){
            if(used[i] >n){
                continue;
            }
            if(i == 0){
                path.offerLast('(');
                used[i]++;
                backtrace(n);
                path.pollLast();
                used[i]--;
            }else{
                path.offerLast(')');
                used[i]++;
                backtrace(n);
                path.pollLast();
                used[i]--;
            }
            
        }
    }

    public boolean helper(Deque<Character> path){
        Deque<Character> stack = new LinkedList<>();
        for(char c:path){
            if(c == '('){
                stack.offerLast(')');
            }else{
                if(stack.isEmpty()){
                    return false;
                }else{
                    stack.pollLast();
                }
            }
        }
        if(!stack.isEmpty()){
            return false;
        }
        return true;

}
45. 组合总成：给你一个无重复元素的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有不同组合，并以列表形式返回。你可以按任意顺序返回这些组合。candidates 中的同一个数字可以无限制重复被选取。如果至少一个数字的被选数量不同，则两种组合是不同的。

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();
    int sum = 0;
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
       backtrace(candidates,target,0);
       return res;
    }
    public void backtrace(int[] candidates, int target,int begin){
        if(sum > target){
            return;
        }
        if(sum == target){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = begin;i < candidates.length;i++){
            path.offerLast(candidates[i]);
            sum += candidates[i];
            backtrace(candidates,target,i);
            path.pollLast();
            sum -= candidates[i];
        }
    }

    
}

电话号码组合：

class Solution {
    List<String> res = new ArrayList<>();
    Deque<Character> path = new LinkedList<>();
    String[] number = {"abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
   
    public List<String> letterCombinations(String digits) {
        if(digits.length() == 0){
            return new ArrayList();
        }
        char[] chars = digits.toCharArray();
        backtrace(chars,0);
        return res;
    }

    public void backtrace(char[] digits,int index){
        if(index == digits.length){
            StringBuilder sb = new StringBuilder();
            for(char c:path){
                sb.append(c);
            }
            res.add(sb.toString());
            return;
        }
        for(int i = 0;i < number[digits[index]-'0'-2].length();i++){
            path.offerLast(number[digits[index]-'0'-2].charAt(i));
            backtrace(digits,index+1);
            path.pollLast();
        }
    }
   
    
}

子集：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();
    public List<List<Integer>> subsets(int[] nums) {
        backtrace(nums,0);
        return res;
    }

    public void backtrace(int[] nums,int index){
        res.add(new ArrayList(path));

        for(int i = index;i <nums.length;i++){
            path.offerLast(nums[i]);
            backtrace(nums,i+1);
            path.pollLast();
        }
    }
    

    
}

全排列：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    Deque<Integer> path = new LinkedList<>();
    boolean[] used = new boolean[21];
    public List<List<Integer>> permute(int[] nums) {
        backtrace(nums);
        return res;
    }
    public void backtrace(int[] nums){
        if(path.size() == nums.length){
            res.add(new ArrayList(path));
            return;
        }

        for(int i = 0;i < nums.length;i++){
            if(used[nums[i]+10]){
                continue;
            }else{
                path.offerLast(nums[i]);
                used[nums[i]+10] = true;
                backtrace(nums);
                path.pollLast();
                used[nums[i] +10] =false;
            }
        }
    }
    

    
}

在排序数组中查找给定元素的起始和结尾位置：

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;
        int first = -1;
        int last = -1;
        // 找第一个等于target的位置
        while (left <= right) {
            int middle = (left + right) / 2;
            if (nums[middle] == target) {
                first = middle;
                right = middle - 1; //重点
            } else if (nums[middle] > target) {
                right = middle - 1;
            } else {
                left = middle + 1;
            }
        }

        // 最后一个等于target的位置
        left = 0;
        right = nums.length - 1;
        while (left <= right) {
        int middle = (left + right) / 2;
        if (nums[middle] == target) {
            last = middle;
            left = middle + 1; //重点
        } else if (nums[middle] > target) {
            right = middle - 1;
        } else {
            left = middle + 1;
        }
        }

        return new int[]{first, last};
    }
}

搜索旋转排序数组：先判断mid左右哪段有序，再判断target在不在有序范围内。在有序范围内，则给某个边界赋值mid+1或-1。直至left > right。

class Solution {
    public int search(int[] nums, int target) {
        int left =0,right = nums.length - 1;
        while(left < right){
            int mid = (left + right) /2;
            if(nums[mid] == target ){
                return mid;
            }
            if(nums[mid] > nums[right]){
                //说明[left,mid]肯定有序
                if(target>=nums[left]&&target < nums[mid]){
                    right = mid -1;
                }else{
                    left = mid +1;
                }

            }else{
                //[mid,right]肯定有序
                if(target > nums[mid] && target <= nums[right]){
                    left = mid+1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return nums[left] ==target?left:-1;
    }
}

寻找旋转排序数组中的最小值:同理根据mid和right大小判断哪段有序，再把有序中的最小值和res比较，然后赋值为mid+1或-1.

class Solution {
    public int findMin(int[] nums) {
        int left = 0,right = nums.length -1;
        int res = Integer.MAX_VALUE;
        
        while(left <= right){
            int mid = (left + right) /2;
            if(nums[mid] < nums[right]){
                //[mid,right]有序
                res = Math.min(res,nums[mid]);
                right = mid -1;
            }else{
                res= Math.min(res,nums[left]);
                left = mid + 1;
            }
        }

        return res;

    }
}

找两个正序数组中位数：helper函数求两个有序数组中第K大的数。每次比较A与B中第k/2个数即比较cindex=index+k/2-1，忽略较小的一个的这k/2个数，即有效下标起始值为cindex+1。然后k= k - cindex +1。直至k==1或者index越界。

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int len1 = nums1.length,len2 = nums2.length;
        if((len1 + len2) %2 ==1){
            return helper(nums1,nums2,(len1 + len2 ) /2+1);
        }else{
            int m = helper(nums1,nums2,(len1 + len2) /2);
            int n = helper(nums1,nums2,(len1 + len2) /2+1);
            return (m+n)/2.0;
        }
    }

    public int helper(int[] nums1,int[] nums2,int k){
        

        int index1 =0,index2 = 0;
        while(true){
            if(index1 == nums1.length){
                return nums2[index2 + k -1];
            }
            if(index2 == nums2.length){
                return nums1[index1 + k - 1];
            }

            if(k == 1){
                return Math.min(nums1[index1],nums2[index2]);
            }

            int cindex1 = Math.min(index1+k/2,nums1.length) -1;
            int cindex2 = Math.min(index2+k/2,nums2.length) -1;

            if(nums1[cindex1] <= nums2[cindex2]){
                k = k -(cindex1 - index1 + 1);
                index1 = cindex1 +1;
            }else{
                k = k - (cindex2 - index2 +1);
                index2 = cindex2 +1;
            }

        }
    }
}

最小栈：

class MinStack {
    PriorityQueue<Integer> pq = new PriorityQueue<>();
    Deque<Integer> numStack = new LinkedList<>();
    public MinStack() {
       
    }
    
    public void push(int val) {
        pq.add(val);
        numStack.offerLast(val);
    }
    
    public void pop() {
        pq.remove(top());
        numStack.pollLast();
    }
    
    public int top() {
        return numStack.peekLast();
    }
    
    public int getMin() {
        return pq.peek();
    }
}

字符串解码：从前往后遍历s，遇到0-9让num=num*10+c，遇到字母则sb.append,遇到 [ 则strStack存放sb，sb置新，numStack存放该次num，num置0，遇到】则取出num，再进行num此的sb重复并拼接到strStack中的preSb。最后返回sb。

class Solution {
    
    public String decodeString(String s) {
        StringBuilder sb = new StringBuilder();
        Deque<Integer> numStack = new LinkedList<>();
        Deque<String> strStack = new LinkedList<>();
        int num= 0;
        
        for(int i = 0;i < s.length();i++){
            char c = s.charAt(i);
            if(c >= '0' && c <= '9'){
                num = num*10 + c -'0';
            }else if((c >= 'a' && c <= 'z') || (c >= 'A' && c <= 'Z')){
                sb.append(c);
            }else if(c == '['){
                strStack.offerLast(sb.toString());
                sb = new StringBuilder();
                numStack.offerLast(num);
                num = 0;
            }else{
                StringBuilder preSb = new StringBuilder().append(strStack.pollLast());
                int times = numStack.pollLast();
                for(int j = 0;j < times;j++){
                    preSb.append(sb);
                }
                sb = preSb;
            }
        }
        return sb.toString();
    }

    
}

每日温度：求下一个第一个更高温度出现在几天后（求右边第一个更大数的下标）。单调栈存下标，当前num[i]大于num[last]则ans[polllast]=i。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        int[] res= new int[temperatures.length];
        Deque<Integer> stack = new LinkedList<>();
        
        for(int i=0;i < temperatures.length;i++){
            while(!stack.isEmpty()&&temperatures[i] > temperatures[stack.peekLast()]){
                int now = stack.pollLast();
                res[now] = i - now;
            }
            stack.offerLast(i);
        }
        return res;
    }
}

无序数组中第K大元素值：K容量最小堆（PriorityQueue）。当size < k时直接offer，否则判断peek和num[i]，如果peek大则跳过，否则poll，再offer。最后取出peek返回。

public int findKthLargest(int[] nums, int k) {
        final PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int val : nums) {
            queue.add(val);
            if (queue.size() > k)
                queue.poll();
        }
        return queue.peek();
    }

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
51. 前 K 个高频元素：频率用hashmap统计，前K用最小堆，最后遍历最小堆。

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        int[] res = new int[k];
        int i = 0;
        Map<Integer,Integer> map = new HashMap<>();
        for(int n:nums){
            map.put(n,map.getOrDefault(n,0)+1);
        }
        PriorityQueue<Map.Entry<Integer,Integer>> pq = new PriorityQueue<>(new Comparator<Map.Entry<Integer,Integer>>(){
            public int compare(Map.Entry<Integer,Integer> o1,Map.Entry<Integer,Integer> o2){
                return o1.getValue() - o2.getValue();
            }
        });

        for(Map.Entry<Integer,Integer> e:map.entrySet()){
            if(pq.size() < k){
                pq.offer(e);
            }else{
                if(e.getValue() > pq.peek().getValue()){
                    pq.poll();
                    pq.offer(e);
                }
            }
        }

        for(Map.Entry<Integer,Integer> e:pq){
            res[i++] = e.getKey();
        }
        return res;
    }
}

买卖股票：

public class Solution {

    public int maxProfit(int[] prices) {
        int len = prices.length;
        // 特殊判断
        if (len < 2) {
            return 0;
        }
        int[][] dp = new int[len][2];

        // dp[i][0] 下标为 i 这天结束的时候，不持股，手上拥有的现金数
        // dp[i][1] 下标为 i 这天结束的时候，持股，手上拥有的现金数

        // 初始化：不持股显然为 0，持股就需要减去第 1 天（下标为 0）的股价
        dp[0][0] = 0;
        dp[0][1] = -prices[0];

        // 从第 2 天开始遍历
        for (int i = 1; i < len; i++) {
            dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
        }
        return dp[len - 1][0];
    }
}

跳跃游戏：判断能否到达。nums最大跳跃长度。遍历nums，用end记录最长下标，当end>= i时end和i+nums[i]比较取最大。

class Solution {
    public boolean canJump(int[] nums) {
       boolean[] path = new boolean[nums.length];
       path[0] = true;

        for(int i = 0;i < nums.length - 1 && path[i];i++){
            for(int j = 1; j <= nums[i];j++){
                if(i + j < path.length){
                    path[i+j] = true;
                }
                
            }
        }
        return path[nums.length - 1];
    }
}

跳跃游戏进阶：返回跳跃次数的最小值。用end记录当前跳跃最长下标，maxPos记录已知可达最大下标，当i==end时，说明当前次的跳跃已经知道跳到哪maxPo最大了，所以end=maxPo，step++。

class Solution {
    
    public int jump(int[] nums) {
        if(nums.length == 1){
            return 0;
        }
        int res = 0;
        int last = find(nums,nums.length - 1);
        res++;
        while(last >0){
            last = find(nums,last);
            res++;
        }
        return res;
    }

    public int find(int[] nums,int index){
        for(int i = 0;i < nums.length - 1;i++){
            if(nums[i] + i >= index){
                return i;
            }
        }
        return -1;
    }
}

划分字母区间：int[] last存字母最后出现下标。用start，end记录当前子串下标，遍历s,end更新为last[s[i] - ‘a’]和end的最大值，直至i==end，res.add，然后start=end+1.

class Solution {
    public List<Integer> partitionLabels(String s) {
        int l = s.length();
        int[] last = new int[26];
        for(int i = 0; i < l;i++){
            last[s.charAt(i) - 'a'] = i;
        }

        List<Integer> res = new ArrayList<>();
        int start = 0,end = 0;
        for(int i = 0;i < l;i++){
            end = Math.max(end,last[s.charAt(i) - 'a']);
            if(end == i){
                res.add(end - start + 1);
                start = end + 1;
            }
        }
        return res;
    }
}

打家劫舍：相邻房间不能抢。dp[i]为抢前i家的最大金钱。dp[i] = max(dp[i-1]，dp[i-2]+nums[i-1])。

class Solution {
    public int rob(int[] nums) {
        int l = nums.length;
        int[] dp = new int[l+1];
        dp[0] = 0;
        dp[1] = nums[0];
        for(int i = 2;i < dp.length;i++){
            dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]);
        }
        return dp[l];
    }
}

返回和为 n 的完全平方数的最少数量：dp[i]和为i的完全平方数最少数量。完全背包问题，先物品再背包。i从1，ii<=n,i++。dp[j] = min(dp[i],dp[j-ii]+1)。

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n+1];
        for(int i = 0;i < dp.length;i++){
            dp[i] = i;
        }
        for(int i = 2;i * i <= n;i++){
            for(int j = 0;j <= n;j++){
                if(i*i <= j){
                    dp[j] = Math.min(dp[j - i*i]+1,dp[j]);
                }
                
            }
        }
        return dp[n];
    }
}

计算并返回可以凑成总金额所需的最少的硬币个数：完全背包。先物品再背包。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount+1];
        Arrays.fill(dp,amount+1);
        dp[0] = 0;
        for(int i = 0;i < coins.length;i++){
            for(int j = 1;j <=amount;j++){
                if(j >= coins[i]){
                    dp[j] = Math.min(dp[j-coins[i]]+1,dp[j]);
                }
                
            }
        }
        return dp[amount] == amount+1?-1:dp[amount];

    }
}

单词拆分：如果能用字符串数组中的某些字符串拼出s则返回true。

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[] dp = new boolean[s.length()+1];
        dp[0] = true;
        for(int i = 1; i <= s.length();i++){
            for(int j = 0;j < wordDict.size();j++){
                String temp = wordDict.get(j);
                if(i>=temp.length()){
                    dp[i] = dp[i] ||(dp[i-temp.length()] && isOk(temp,s,i-temp.length()));
                }
            }
        }
        
        return dp[s.length()];
    }

    public boolean isOk(String temp,String s,int start){
        for(int i = 0;i < temp.length();i++){
            if(start+i >= s.length()){
                return false;
            }
            if(temp.charAt(i) != s.charAt(start+i)){
                return false;
            }
        }
        return true;
    }
    
}

最长严格递增子序列的长度:dp[i] 以nums[i]结尾的递增子序列的长度.dp[i] = for(dp[j]+1,dp[i])

class Solution {
    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];
        Arrays.fill(dp,1);
        int res = 1;
        for(int i = 1;i < nums.length;i++){
            for(int j = 0;j < i;j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i],dp[j]+1);
                }
            }
            res = Math.max(dp[i],res);
        }
        return res;
        
    }
}

乘积最大子数组：

class Solution {
    public int maxProduct(int[] nums) {
        int[][] dp = new int[nums.length][2];
        int res= nums[0];
        for(int i = 0;i <nums.length;i++){
            dp[i][0]=nums[i];
            dp[i][1]=nums[i];
        }
        for(int i = 1;i <nums.length;i++){
            int temp0 = nums[i]*dp[i-1][0];
            int temp1 = nums[i]*dp[i-1][1];
            dp[i][0] = Math.min(dp[i][0],Math.min(temp0,temp1));
            dp[i][1] = Math.max(dp[i][1],Math.max(temp0,temp1));
            res = Math.max(res,dp[i][1]);
        }
        return res;
    }
}

分割等和子集：dp[i]是否达到和为i。有限背包，先物品，再倒遍历背包。dp【i】=dp【i】|| dp【i-nums【j】】

class Solution {
    
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for(int n:nums){
            sum = sum + n;
        }
        if(sum % 2 !=0){
            return false;
        }

        int target = sum / 2;

        boolean[] dp = new boolean[target+1];
        dp[0] = true;
        for(int i = 0;i < nums.length;i++){
            for(int j = target;j >= nums[i];j--){
                dp[j] = dp[j] || dp[j-nums[i]];
            }
        }
        return dp[target];
    }
    
}

最长有效括号：dp【i】以下标i结尾的最长有效括号长度。当s【i】==）时，判断i-dp【i-1】-1》0 &&s【i-dp【i-1】-1】是否（。如果是则dp【i】=2+dp【i-1】+（i-dp【i-1】-2 >0?dp[i-dp【i-1】-2 ]:0）。

class Solution {
    
    public int longestValidParentheses(String s) {
        if(s.length() <= 1){
            return 0;
        }
        Deque<Integer> stack = new LinkedList<>();
        int res = 0;
        int start = 0;
        for(int i = 0; i < s.length();i++){
            if(s.charAt(i) == '('){
                stack.offerLast(i);
            }else{
                if(stack.isEmpty()){
                    start = i+1;
                    continue;
                }
                stack.pollLast();
                if(stack.isEmpty()){
                    res = Math.max(res,i - start+1);
                }else{
                    res = Math.max(res,i - (stack.peekLast()+1) + 1);
                }
            }

        }
        return res;
        
    }

    
}

最长回文子串：dp[i][j]表示下标i到j是回文子串。外for从倒数第二个字母开始–，内for从i+1开始++。当i和j的字母不同时，dpij肯定是false，如果相同：如果j-i==1时，为true，否则就是dpi+1j-1;

class Solution {
    public String longestPalindrome(String s) {
        boolean[][] dp = new boolean[s.length()][s.length()];
        int l = 0,r = 0;
        for(int i = 0;i < s.length();i++){
            dp[i][i] = true;
        }

        for(int i = s.length() - 2;i >=0;i--){
            for(int j =i +1;j <s.length();j++){
                if(s.charAt(i) != s.charAt(j)){
                    
                    continue;
                }else{
                    if(j-i == 1){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i+1][j-1];
                    }
                }
                if(dp[i][j]&&j - i > r - l){
                    l = i;
                    r = j;
                }
            }
        }
        return s.substring(l,r+1);
    }
}

最长公共子序列：dpij表示为text1中前i个和text2中前j个时最长公共子序列长度。dpij和谁有关系：dpi-1j，dpij-1，dpi-1j-1，t1i-1,t2j-1。如果1i-1t2j-1，那么dpij = dpi-1j-1 +1;如果不，那么dpij = max dpi-1j，dpij-1

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int l1 = text1.length(),l2 = text2.length();
        int[][] dp =new int[l1+1][l2+1];
        for(int i = 1; i<= l1;i++){
            dp[i][0] = 0;
        }
        for(int i = 1; i<= l2;i++){
            dp[0][i] = 0;
        }
        for(int i = 1;i<=l1;i++){
            for(int j = 1;j <= l2;j++){
                if(text1.charAt(i-1) == text2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1] +1;
                }else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[l1][l2];
    }
}

word1 转换成 word2 所使用的最少操作数：增删改，dpij为将前i和前j的w1转为w2最少操作数。

class Solution {
    public int minDistance(String word1, String word2) {
        int l1 = word1.length(),l2 = word2.length();
        int[][] dp = new int[l1+1][l2+1];
        dp[0][0] = 0;
        for(int i = 1; i <= l1;i++){
            dp[i][0] = i;
        }
        for(int i = 1; i <= l2;i++){
            dp[0][i] = i;
        }
        for(int i = 1;i <= l1;i++){
            for(int j = 1;j <= l2;j++){
                if(word1.charAt(i-1) == word2.charAt(j-1)){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = Math.min(dp[i-1][j-1]+1,Math.min(dp[i-1][j] + 1,dp[i][j-1] + 1));
                }
            }
        }
        return dp[l1][l2];
    }
}

排序：

import java.util.Arrays;

public class SortingAlgorithms {

    // 冒泡排序
    public static void bubbleSort(int[] arr) {
        int n = arr.length;
        boolean swapped;
        for (int i = 0; i < n - 1; i++) {
            swapped = false;
            for (int j = 0; j < n - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    // swap arr[j+1] and arr[i]
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    swapped = true;
                }
            }
            // 如果没有发生交换，数组已经有序
            if (!swapped) break;
        }
    }

    // 选择排序
    public static void selectionSort(int[] arr) {
        int n = arr.length;

        for (int i = 0; i < n - 1; i++) {
            // 找到未排序序列中的最小元素
            int minIdx = i;
            for (int j = i + 1; j < n; j++)
                if (arr[j] < arr[minIdx])
                    minIdx = j;

            // 将找到的最小元素与第一个未排序元素交换
            int temp = arr[minIdx];
            arr[minIdx] = arr[i];
            arr[i] = temp;
        }
    }

    // 插入排序
    public static void insertionSort(int[] arr) {
        int n = arr.length;
        for (int i = 1; i < n; ++i) {
            int key = arr[i];
            int j = i - 1;

            while (j >= 0 && arr[j] > key) {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = key;
        }
    }

    // 快速排序
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);

            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = (low - 1); // 较小元素的索引
        for (int j = low; j < high; j++) {
            if (arr[j] <= pivot) {
                i++;

                // 交换arr[i]和arr[j]
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        // 交换arr[i+1]和arr[high] (或pivot)
        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;

        return i + 1;
    }

    // 归并排序
    public static void mergeSort(int[] arr, int l, int r) {
        if (l < r) {
            int m = (l + r) / 2;

            mergeSort(arr, l, m);
            mergeSort(arr, m + 1, r);

            merge(arr, l, m, r);
        }
    }

    private static void merge(int[] arr, int l, int m, int r) {
        int n1 = m - l + 1;
        int n2 = r - m;

        int[] L = new int[n1];
        int[] R = new int[n2];

        for (int i = 0; i < n1; ++i)
            L[i] = arr[l + i];
        for (int j = 0; j < n2; ++j)
            R[j] = arr[m + 1 + j];

        int i = 0, j = 0;

        int k = l;
        while (i < n1 && j < n2) {
            if (L[i] <= R[j]) {
                arr[k] = L[i];
                i++;
            } else {
                arr[k] = R[j];
                j++;
            }
            k++;
        }

        while (i < n1) {
            arr[k] = L[i];
            i++;
            k++;
        }

        while (j < n2) {
            arr[k] = R[j];
            j++;
            k++;
        }
    }

    public static void main(String[] args) {
        int[] arr = {64, 34, 25, 12, 22, 11, 90};
        
        // 测试上述任意排序算法，例如：
        // bubbleSort(arr);
        // selectionSort(arr);
        // insertionSort(arr);
        // quickSort(arr, 0, arr.length-1);
        mergeSort(arr, 0, arr.length - 1);
        
        System.out.println("Sorted array: " + Arrays.toString(arr));
    }
}

单例模式

1、饿汉式

Public class Singleton(){
	private Singleton(){};
	
	private static final Singleton instance = new Singleton();
	public Singleton getInstance(){
		return instance;	
	}

2、双重检查

public class Singleton(){
	private Singleton(){};
	private static final Singleton instace;
	public static Singleton getInstance(){
		if(instance == null){
			synchronized(Singleton.class){
				if(instance == null){
					instance = new Singleton();
				}
			}
		}
		return instance;
	}
}

3、静态内部类

public class Singleton(){
	private Singleton(){};
	private static class SingletonHolder(){
		public static final INSTANCE= new Singleton();
	}
	public static Singleton getInstance(){
		return SingletonHolder.INSTANCE;
	}
}

4、枚举

public enum Singleton(){
	INSTANCE;
}