认真学习数据结构之堆

流烟默

已于 2022-08-09 13:01:18 修改

阅读量2.5k

点赞数

CC 4.0 BY-SA版权

分类专栏：数据结构 | 算法文章标签：堆

于 2016-10-10 17:20:05 首次发布

本文链接：https://blog.youkuaiyun.com/J080624/article/details/52779654

数据结构 | 算法专栏收录该内容

41 篇文章

订阅专栏

【1】什么是堆？

堆（heap）是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

堆中某个结点的值总是不大于(大顶堆)或不小于其父结点的值(小顶堆)；
堆总是一棵完全二叉树。

将根结点最大的堆叫做最大堆或大根堆，根结点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。

堆是非线性数据结构，相当于一维数组，有两个直接后继。

堆的定义如下：n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时，称之为堆。
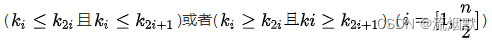
在这里插入图片描述

若将和此次序列对应的一维数组（即以一维数组作此序列的存储结构）看成是一个完全二叉树，则堆的含义表明，完全二叉树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。

由此，若序列{k1,k2,…,kn}是堆，则堆顶元素（或完全二叉树的根）必为序列中n个元素的最小值（或最大值）。

如下所示是以数组存储的小顶堆

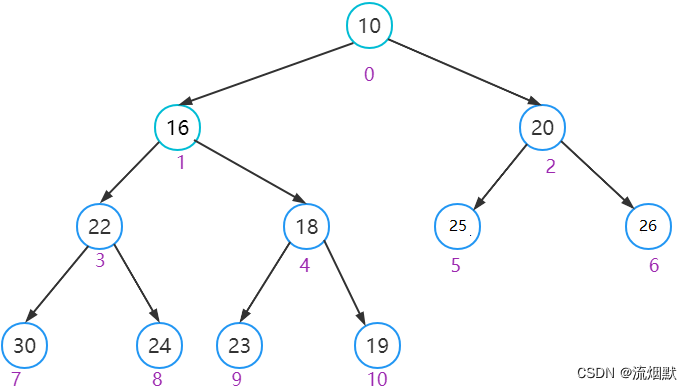
在这里插入图片描述
n个结点的堆，高度d=logn。根为第0层，则第 n 层结点个数为 2ⁿ，考虑一个元素在堆中向下移动的距离，这种算法时间代价为O(n)。

由于堆有㏒n层深，插入结点、删除普通元素和删除最小元素的平均时间代价和时间复杂度都是O(logn)。

完全二叉树与满二叉树

完全二叉树的特点：叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。

一棵深度为 n 且有2ⁿ-1 个结点的二叉树称为满二叉树。

根据二叉树的性质2, 满二叉树每一层的结点个数都达到了最大值, 即满二叉树的第 i 层上有 2^(i-1)个结点 (i≥1,最顶层称为第 1 层) 。

需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

完全二叉树适合使用顺序结构存储，通常我们使用数组来存储。

下标关系

已知双亲 (parent) 的下标，则：

左孩子(left)下标 = 2 * parent + 1;
右孩子(right) 下标 = 2 * parent + 2;

已知孩子（不区分左右） (child) 下标，则双亲(parent) 下标 = (child - 1) / 2。

【2】小顶堆

小顶堆即根节点为最小时，叶子结点不小于父节点的完全二叉树。我们以小顶堆分析其常见方法。

① 建堆

假设有一个数组：10 16 20 22 23 24 18 19 25 26 30，那么如何构建为堆呢？首先我们构建为一颗二叉树(很明显其不是一个堆)：

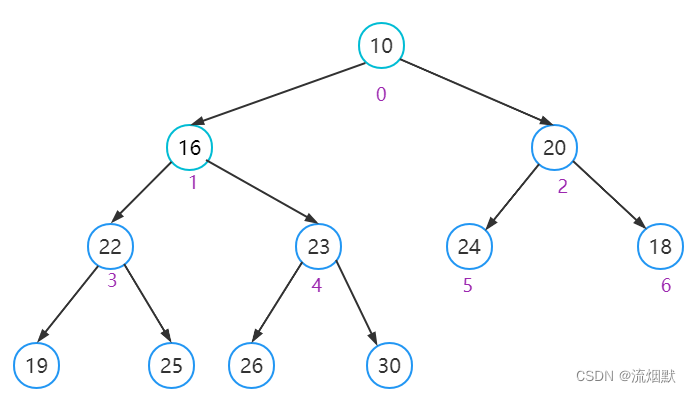
在这里插入图片描述

为了构建称为一个堆，那么我们需要调整每棵子树，使其满足叶子结点小于父结点的形态。这里的思想就是遍历每一个父节点进行向下调整即可。这里我们从最后一个父节点开始调整：

// size表示数组中元素个数
private void heapify() {
    for (int i = (size >>> 1) - 1; i >= 0; i--)
        siftDown(i, (E) queue[i]);
}

② 向下调整

也就是从当前结点位置一路往下遍历叶子结点，直到最后一层。什么时候触发向下调整呢，比如移除元素的时候。这时候会把末尾结点填充到移除位置，然后从移除位置开始触发向下调整。每一次调整K=k<<1+ or k=k<<1+2。

private void siftDownComparable(int k, E x) {
	// 调整的结点值
    Comparable<? super E> key = (Comparable<? super E>)x;
    // 取数组长度的中间值
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
    	//左叶子结点
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        //右叶子结点
        int right = child + 1;
        //判断左右叶子结点大小，并获取左右叶子结点最小值c
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        //父节点与叶子结点最小值进行对比    
        if (key.compareTo((E) c) <= 0)
            break;
        // 父节点与叶子结点最小值交换    
        queue[k] = c;
        // 更新k 为叶子结点最小值的下标，继续下次循环
        k = child;
    }
    //目标结点放到k处
    queue[k] = key;
}

这里 int half = size >>> 1; while (k < half) {}是个优化。当k>=half时，自动结束循环。

为什么呢？因为此时必然已经索引到了最后一层叶子结点！因为最后按照完全二叉树来说，最后一个父节点必然是(length>>>1)-1，所以k最多遍历到最后一个父节点，这时就意味着已完成了可能的遍历。

假设满二叉树有 i 层(i>=1,最顶层为第一层)，那么每层结点个数：2^0，2^1，2^2，2^3，2……i-3,2^i-2,2^i-1,那么求和如下：
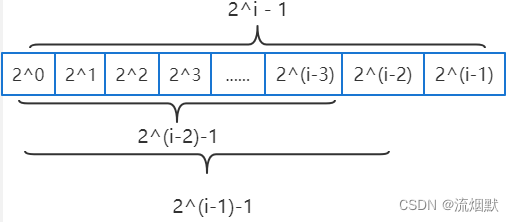
在这里插入图片描述
因为这里的堆其并不一定是满二叉树(但一定是完全二叉树)，那么结点总数为：2^(i-1) --- 2^i-1,其half范围是[2^(i-2),2^(i-1)-1]。以half=2^(i-1)-1为例(也就是满二叉树)，那么索引位置为2^(i-1)-2处刚好是最后一个父节点。而2^(i-2)呢，则是最后一层只有一个叶子结点的情况，此时当然是倒数第二层最左侧的结点了，也就是2^(i-2)-1这个索引位置。

另外，length/2是完全二叉树第一个叶节点的位置。所以length/2 -1 则是最后一个父节点咯。

这也能够证明为什么(length>>>1)-1是最后一个父节点了，这也为什么while的条件是k<half。

③ 向上调整

什么时候向上调整呢？当你插入一个元素的时候，通常是默认插入末尾。这时候会从末尾位置一直向父节点追溯与parent进行对比，直到根节点为止。

private void siftUpComparable(int k, E x) {
	// 目标结点进行类型转型
    Comparable<? super E> key = (Comparable<? super E>) x;
    //还没有到根节点
    while (k > 0) {
    	//获取父节点
        int parent = (k - 1) >>> 1;
        //获取父节点值并进行对比
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0)
            break;
        //如果小于父节点则进行交互    
        queue[k] = e;
        k = parent;
    }
    //放到目标位置
    queue[k] = key;
}

【3】堆排序

① 算法思想

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

算法步骤：

将初始待排序关键字序列（R1，R2 … .Rn）构建成大顶堆，此堆为初始的无序区;
将堆顶元素R [1]与最后一个元素 [R [n]的交换，此时得到新的无序区（R1，R2，… Rn中-1）和新的有序区（RN），且满足R[1,2，…，N-1] <= R [N];
由于交换后新的堆顶R [1]可能违反堆的性质，因此需要对当前无序区（R1，R2，… Rn中-1）调整为新堆，然后再次将R [1]与无序区最后一个元素交换，得到新的无序区（R1，R2 … .Rn-2）和新的有序区（RN-1，RN）的。不断重复此过程直到有序区的元素个数为ñ -1，则整个排序过程完成。

② java实现&大顶堆

public class HeapSort {
    static int[] queue={91,60,96,13,35,65,46,65,10,30,20,31,77,81,22};
    static int length=queue.length;

//进行堆化，从最后一个父节点开始，向下调整
    private static void heapify(){
        for (int i = (length >>> 1) - 1; i >= 0; i--)
            siftDown(i,  queue[i]);
    }

//向下调整为一个大顶堆
    private static void siftDown(int k, int e) {
        int half=length>>>1;
        while (k<half){
            int child=(k<<1)+1;
            int right=child+1;
            //保存左右叶子最大值
            int temp=queue[child];
            if(right<length&&temp<queue[right]){
                temp=queue[child=right];
            }
            if(e>=temp){
                break;
            }
            queue[k]=temp;
            k=child;
        }
        queue[k]=e;
    }
//排序--先进行堆化，然后从length-1位置处开始、交换、调整
    private static void sort(){
        heapify();
        for(int j = length-1;j>=0;j--){
            swap(queue,0,j);
            length--;
            siftDown(0,queue[0]);
        }
    }

    private static void swap(int[] queue, int i, int j) {
        int temp=queue[j];
        queue[j]=queue[i];
        queue[i]=temp;
    }
    public static void main(String[] args){
        sort();
        Arrays.stream(queue).forEach(System.out::println);
    }

}